Jak pomnożyć dwie liczby o różnych potęgach. Formuły potęg i pierwiastków. Dalsze rozwiązywanie typowych problemów

Oczywiście liczby z potęgami można dodawać jak inne wielkości , dodając je jeden po drugim wraz z ich znakami.

Zatem suma a 3 i b 2 to a 3 + b 2 .
Suma a 3 - b n i h 5 - d 4 to 3 - b n + h 5 - d 4 .

Szanse te same moce tych samych zmiennych można dodawać lub odejmować.

Zatem suma 2a 2 i 3a 2 to 5a 2 .

Jest też oczywiste, że jeśli weźmiemy dwa kwadraty a, lub trzy kwadraty a, lub pięć kwadratów a.

Ale stopnie różne zmienne oraz różne stopnie identyczne zmienne, należy dodać, dodając je do ich znaków.

Zatem suma a 2 i a 3 jest sumą a 2 + a 3 .

Jest oczywiste, że kwadrat a i sześcian a nie jest ani dwukrotnością kwadratu a, ale dwukrotnością sześcianu a.

Suma a 3 b n i 3a 5 b 6 to a 3 b n + 3a 5 b 6 .

Odejmowanie uprawnienia są wykonywane w taki sam sposób, jak dodawanie, z tym wyjątkiem, że znaki oddzielenia muszą być odpowiednio zmienione.

Lub:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 - 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6

Mnożenie potęgi

Liczby z potęgami można mnożyć, podobnie jak inne wielkości, pisząc je jedna po drugiej, z lub bez znaku mnożenia między nimi.

Tak więc wynik pomnożenia a 3 przez b 2 to a 3 b 2 lub aaabb.

Lub:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 x y 2
a 2 b 3 r 2 ⋅ a 3 b 2 r = a 2 b 3 r 2 za 3 b 2 r

Wynik w ostatnim przykładzie można uporządkować, dodając te same zmienne.
Wyrażenie przyjmie postać: a 5 b 5 y 3 .

Porównując kilka liczb (zmiennych) z potęgami, widzimy, że jeśli pomnoży się dowolne dwie z nich, to otrzymamy liczbę (zmienną) o potędze równej suma stopnie terminów.

A więc a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Tutaj 5 jest potęgą wyniku mnożenia, równą 2 + 3, sumą potęg wyrazów.

A więc n .a m = a m+n .

Dla n , a jest brane jako czynnik tyle razy, ile jest potęgi n;

A m , przyjmuje się jako czynnik tyle razy, ile stopni m jest równe;

Dlatego, potęgi o tych samych podstawach można pomnożyć przez dodanie wykładników.

A więc a 2 .a 6 = a 2+6 = a 8 . Oraz x 3 .x 2 .x = x 3+2+1 = x 6 .

Lub:
4a n ⋅ 2a n = 8a 2n
b 2 r 3 ⋅ b 4 r = b 6 r 4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1

Pomnóż (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Odpowiedź: x 4 - y 4.
Pomnóż (x 3 + x - 5) ⋅ (2x 3 + x + 1).

Ta zasada odnosi się również do liczb, których wykładniki są - negatywny.

1. A więc a -2 .a -3 = a -5 . Można to zapisać jako (1/aa).(1/aaa) = 1/aaaaa.

2. y-n .y-m = y-n-m .

3. a-n .a m = a m-n .

Jeśli a + b pomnożymy przez a - b, wynikiem będzie a 2 - b 2: czyli

Wynik mnożenia sumy lub różnicy dwóch liczb jest równa sumie lub różnicy ich kwadratów.

Jeśli suma i różnica dwóch liczb podniesiona do kwadrat, wynik będzie równy sumie lub różnicy tych liczb w czwarty stopień.

Tak więc (a - y).(a + y) = a 2 - y 2 .
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4 .
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8 .

Podział władz

Liczby z potęgami można dzielić tak jak inne liczby, odejmując od dzielnika lub umieszczając je w postaci ułamka.

Więc a 3 b 2 podzielone przez b 2 to a 3 .

Lub:
$\frac(9a^3y^4)(-3a^3) = -3y^4$
$\frac(a^2b + 3a^2)(a^2) = \frac(a^2(b+3))(a^2) = b + 3$
$\frac(d\cdot (a - h + y)^3)((a - h + y)^3) = d$

Zapisanie 5 podzielonej przez 3 wygląda jak $\frac(a^5)(a^3)$. Ale to jest równe 2 . W serii liczb
za +4 , za +3 ​​, za +2 , za +1 , za 0 , za -1 , za -2 , za -3 , za -4 .
dowolną liczbę można podzielić przez drugą, a wykładnik będzie równy różnica wskaźniki liczb podzielnych.

Dzieląc potęgi o tej samej podstawie, ich wykładniki są odejmowane..

Tak więc y 3: y 2 = y 3-2 = y 1 . Oznacza to, że $\frac(yyy)(yy) = y$.

A n+1:a = a n+1-1 = a n . Oznacza to, że $\frac(aa^n)(a) = a^n$.

Lub:
y2m: ym = ym
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b + y) n-3

Zasada obowiązuje również dla liczb z negatywny wartości stopni.
Wynik dzielenia -5 przez -3 daje -2 .
Również $\frac(1)(aaaaa) : \frac(1)(aaa) = \frac(1)(aaaaa).\frac(aaa)(1) = \frac(aaa)(aaaaa) = \frac (1)(aa)$.

h 2:h -1 = h 2+1 = h 3 lub $h^2:\frac(1)(h) = h^2.\frac(h)(1) = h^3$

Konieczne jest bardzo dobre opanowanie mnożenia i dzielenia potęg, ponieważ takie operacje są bardzo szeroko stosowane w algebrze.

Przykłady rozwiązywania przykładów z ułamkami zawierającymi liczby z potęgami

1. Zmniejsz wykładniki w $\frac(5a^4)(3a^2)$ Odpowiedź: $\frac(5a^2)(3)$.

2. Zmniejsz wykładniki w $\frac(6x^6)(3x^5)$. Odpowiedź: $\frac(2x)(1)$ lub 2x.

3. Zmniejsz wykładniki 2/a 3 i a-3/a -4 i doprowadź do wspólnego mianownika.
a 2 .a -4 to pierwszy licznik -2.
a 3 .a -3 to 0 = 1, drugi licznik.
a 3 .a -4 to -1 , wspólny licznik.
Po uproszczeniu: a -2 /a -1 i 1/a -1 .

4. Zmniejsz wykładniki 2a 4 /5a 3 i 2 /a 4 i doprowadź do wspólnego mianownika.
Odpowiedź: 2a 3 / 5a 7 i 5a 5 / 5a 7 lub 2a 3 / 5a 2 i 5/5a 2.

5. Pomnóż (a 3 + b)/b 4 przez (a - b)/3.

6. Pomnóż (a 5 + 1)/x 2 przez (b 2 - 1)/(x + a).

7. Pomnóż b 4 /a -2 przez h -3 /x i a n /y -3 .

8. Podziel 4 /y 3 przez 3 /y 2 . Odpowiedź: a/y.

9. Podziel (h 3 - 1)/d 4 przez (d n + 1)/h.

Jeśli chcesz podnieść określoną liczbę do potęgi, możesz użyć . Teraz przyjrzymy się bliżej właściwości stopni.

Liczby wykładnicze otwierają ogromne możliwości, pozwalają nam zamienić mnożenie na dodawanie, a dodawanie jest znacznie łatwiejsze niż mnożenie.

Na przykład musimy pomnożyć 16 przez 64. Iloczynem tych dwóch liczb jest 1024. Ale 16 to 4x4, a 64 to 4x4x4. Czyli 16 razy 64=4x4x4x4x4, czyli również 1024.

Liczbę 16 można również przedstawić jako 2x2x2x2, a 64 jako 2x2x2x2x2x2, a jeśli pomnożymy, ponownie otrzymamy 1024.

Użyjmy teraz reguły. 16=4 2 lub 2 4 , 64=4 3 lub 2 6 , a 1024=6 4 =4 5 lub 2 10 .

Zatem nasz problem można zapisać w inny sposób: 4 2 x4 3 =4 5 lub 2 4 x2 6 =2 10 i za każdym razem otrzymujemy 1024.

Możemy rozwiązać wiele podobnych przykładów i zobaczyć, że mnożenie liczb przez potęgi redukuje się do dodawanie wykładników, lub oczywiście wykładnik, pod warunkiem, że podstawy współczynników są równe.

W ten sposób możemy, bez mnożenia, od razu powiedzieć, że 2 4 x2 2 x2 14 \u003d 2 20.

Ta zasada obowiązuje również przy dzieleniu liczb przez potęgi, ale w tym przypadku e wykładnik dzielnika jest odejmowany od wykładnika dywidendy. Zatem 2 5:2 3 =2 2 , co w zwykłych liczbach jest równe 32:8=4, czyli 2 2 . Podsumujmy:

a m x a n \u003d a m + n, a m: a n \u003d a m-n, gdzie m i n są liczbami całkowitymi.

Na pierwszy rzut oka może się wydawać, że mnożenie i dzielenie liczb przez potęgi niezbyt wygodne, ponieważ najpierw musisz przedstawić liczbę w formie wykładniczej. Nie jest trudno przedstawić liczby 8 i 16 w tej formie, czyli 2 3 i 2 4, ale jak to zrobić z liczbami 7 i 17? Lub co robić w przypadkach, gdy liczba może być reprezentowana w formie wykładniczej, ale podstawy wyrażeń wykładniczych liczb są bardzo różne. Na przykład 8×9 to 2 3 x 3 2 , w takim przypadku nie możemy zsumować wykładników. Ani 2 5 ani 3 5 nie jest odpowiedzią, ani odpowiedzią między nimi.

Czy w takim razie w ogóle warto zawracać sobie głowę tą metodą? Zdecydowanie warto. Daje ogromne korzyści, zwłaszcza przy skomplikowanych i czasochłonnych obliczeniach.

W poprzednim artykule rozmawialiśmy o tym, czym są jednomiany. W tym materiale przeanalizujemy, jak rozwiązywać przykłady i problemy, w których są używane. Rozważymy tutaj takie operacje jak odejmowanie, dodawanie, mnożenie, dzielenie jednomianów i podnoszenie ich do potęgi z wskaźnik naturalny. Pokażemy, jak definiowane są takie operacje, wskażemy podstawowe zasady ich realizacji i jaki powinien być rezultat. Wszystkie założenia teoretyczne, jak zwykle, zostaną zilustrowane przykładami problemów z opisami rozwiązań.

Najwygodniej jest pracować ze standardowym zapisem jednomianów, dlatego wszystkie wyrażenia, które zostaną użyte w artykule, przedstawiamy w formie standardowej. Jeśli początkowo są one ustawione inaczej, zaleca się najpierw doprowadzić je do ogólnie przyjętej formy.

Zasady dodawania i odejmowania jednomianów

Najprostsze operacje, które można wykonać z jednomianami, to odejmowanie i dodawanie. W ogólnym przypadku wynikiem tych działań będzie wielomian (jednomian jest możliwy w niektórych szczególnych przypadkach).

Kiedy dodajemy lub odejmujemy jednomiany, najpierw zapisujemy odpowiednią sumę i różnicę w ogólnie przyjętej formie, po czym upraszczamy wynikowe wyrażenie. Jeśli są podobne terminy, należy je podać, nawiasy należy otworzyć. Wyjaśnijmy na przykładzie.

Przykład 1

Stan: dodaj jednomiany − 3 · x i 2 , 72 · x 3 · y 5 · z .

Rozwiązanie

Zapiszmy sumę oryginalnych wyrażeń. Dodaj nawiasy i umieść między nimi znak plus. Otrzymamy:

(− 3 x) + (2 , 72 x 3 y 5 z)

Kiedy rozszerzamy nawiasy, otrzymujemy - 3 x + 2 , 72 x 3 y 5 z . Jest to wielomian zapisany w standardowej formie, który będzie wynikiem dodania tych jednomianów.

Odpowiadać:(- 3 x) + (2, 72 x 3 do 5 z) = - 3 x + 2, 72 x 3 do 5 z.

Jeśli mamy podane trzy, cztery lub więcej terminów, wykonujemy tę akcję w ten sam sposób.

Przykład 2

Stan: przesuń palcem właściwa kolejność określone operacje na wielomianach

3 a 2 - (- 4 za c) + a 2 - 7 za 2 + 4 9 - 2 2 3 za c

Rozwiązanie

Zacznijmy od otwarcia nawiasów.

3 a 2 + 4 a c + a 2 - 7 a 2 + 4 9 - 2 2 3 a c

Widzimy, że wynikowe wyrażenie można uprościć, redukując podobne terminy:

3 za 2 + 4 za c + za 2 - 7 za 2 + 4 9 - 2 2 3 za c = = (3 za 2 + za 2 - 7 za 2) + 4 za c - 2 2 3 za c + 4 9 = = - 3 za 2 + 1 1 3 za c + 4 9

Mamy wielomian, który będzie wynikiem tego działania.

Odpowiadać: 3 a 2 - (- 4 za c) + a 2 - 7 za 2 + 4 9 - 2 2 3 za c = - 3 za 2 + 1 1 3 za c + 4 9

W zasadzie możemy wykonać dodawanie i odejmowanie dwóch jednomianów, z pewnymi ograniczeniami, tak że otrzymujemy jednomian. Aby to zrobić, konieczne jest przestrzeganie pewnych warunków dotyczących terminów i odejmowanych jednomianów. Opiszemy, jak to się robi w osobnym artykule.

Zasady mnożenia jednomianów

Akcja mnożenia nie nakłada żadnych ograniczeń na mnożniki. Jednomiany do mnożenia nie mogą spełniać żadnych dodatkowych warunków, aby wynik był jednomianem.

Aby wykonać mnożenie jednomianów, musisz wykonać następujące kroki:

1. Nagraj utwór poprawnie.
2. Rozwiń nawiasy w wynikowym wyrażeniu.
3. Jeśli to możliwe, zgrupuj czynniki z tymi samymi zmiennymi i czynniki liczbowe oddzielnie.
4. Wykonaj niezbędne czynności za pomocą liczb i zastosuj właściwość mnożenia potęg o tych samych podstawach do pozostałych czynników.

Zobaczmy, jak to się robi w praktyce.

Przykład 3

Stan: pomnożyć jednomiany 2·x4·y·z i -7 16·t2·x2·z11.

Rozwiązanie

Zacznijmy od składu pracy.

Otwierając w nim nawiasy otrzymujemy:

2 x 4 y z - 7 16 t 2 x 2 z 11

2 - 7 16 t 2 x 4 x 2 y z 3 z 11

Wszystko, co musimy zrobić, to pomnożyć liczby w pierwszych nawiasach i zastosować właściwość potęgi do drugiego. W rezultacie otrzymujemy:

2 - 7 16 t 2 x 4 x 2 y z 3 z 11 = - 7 8 t 2 x 4 + 2 y z 3 + 11 = = - 7 8 t 2 x 6 y z 14

Odpowiadać: 2 x 4 y z - 7 16 t 2 x 2 z 11 = - 7 8 t 2 x 6 y z 14 .

Jeśli w warunku mamy trzy lub więcej wielomianów, mnożymy je za pomocą dokładnie tego samego algorytmu. Kwestię mnożenia jednomianów omówimy bardziej szczegółowo w osobnym materiale.

Zasady podnoszenia jednomianu do potęgi

Wiemy, że iloczyn pewnej liczby identycznych czynników nazywamy stopniem z wykładnikiem naturalnym. Ich liczbę wskazuje liczba w indeksie. Zgodnie z tą definicją podniesienie jednomianu do potęgi jest równoznaczne z pomnożeniem wskazanej liczby identycznych jednomianów. Zobaczmy, jak to się robi.

Przykład 4

Stan: podnieś jednomian − 2 · a · b 4 do potęgi 3 .

Rozwiązanie

Możemy zastąpić potęgowanie przez pomnożenie 3 jednomianów − 2 · a · b 4 . Zapiszmy i uzyskajmy pożądaną odpowiedź:

(− 2 za b 4) 3 = (− 2 za b 4) (− 2 za b 4) (− 2 za b 4) = = ((− 2) (− 2) (− 2)) (a za a) (b 4 b 4 b 4) = − 8 a 3 b 12

Odpowiadać:(− 2 a b 4) 3 = − 8 a 3 b 12 .

Ale co jeśli stopień ma duży wykładnik? Zapisywanie dużej liczby mnożników jest niewygodne. Następnie, aby rozwiązać taki problem, musimy zastosować własności stopnia, a mianowicie własność stopnia iloczynu i własność stopnia w stopniu.

Rozwiążmy problem, który przytoczyliśmy powyżej we wskazany sposób.

Przykład 5

Stan: podnieś − 2 · a · b 4 do trzeciej potęgi.

Rozwiązanie

Znając właściwość stopnia w stopniu, możemy przejść do wyrażenia następującej postaci:

(− 2 a b 4) 3 = (− 2) 3 a 3 (b 4) 3 .

Następnie podnosimy do potęgi - 2 i stosujemy właściwość wykładnika:

(− 2) 3 (a) 3 (b 4) 3 = − 8 a 3 b 4 3 = − 8 a 3 b 12 .

Odpowiadać:− 2 · a · b 4 = − 8 · a 3 · b 12 .

Osobny artykuł poświęciliśmy też podniesieniu jednomianu do potęgi.

Zasady dzielenia jednomianów

Ostatnią czynnością z jednomianami, którą przeanalizujemy w tym materiale, jest podział jednomianu przez jednomian. W rezultacie powinniśmy otrzymać ułamek wymierny (algebraiczny) (w niektórych przypadkach możliwe jest uzyskanie jednomianu). Wyjaśnijmy od razu, że dzielenie przez zero jednomianu nie jest zdefiniowane, ponieważ dzielenie przez 0 nie jest zdefiniowane.

Aby dokonać podziału, musimy zapisać wskazane jednomiany w postaci ułamka i w miarę możliwości je zmniejszyć.

Przykład 6

Stan: podziel jednomian − 9 x 4 y 3 z 7 przez − 6 p 3 t 5 x 2 y 2 .

Rozwiązanie

Zacznijmy od napisania jednomianów w postaci ułamka.

9 x 4 r 3 z 7 - 6 p 3 z 5 x 2 r 2

Ta frakcja może zostać zmniejszona. Po wykonaniu tej czynności otrzymujemy:

3 x 2 y z 7 2 p 3 t 5

Odpowiadać:- 9 x 4 y 3 z 7 - 6 p 3 t 5 x 2 y 2 = 3 x 2 y z 7 2 p 3 t 5 .

Warunki, w jakich w wyniku dzielenia jednomianów otrzymujemy jednomian, są podane w osobnym artykule.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Już wcześniej rozmawialiśmy o tym, czym jest potęga liczby. Ona ma niektóre właściwości, przydatne w rozwiązywaniu problemów: przeanalizujemy je i wszystkie możliwe wykładniki w tym artykule. Pokażemy również na przykładach, jak można je udowodnić i poprawnie zastosować w praktyce.

Przypomnijmy pojęcie stopnia z wykładnikiem naturalnym, które już wcześniej sformułowaliśmy: jest to iloczyn n-tej liczby czynników, z których każdy jest równy a. Musimy też pamiętać, jak poprawnie pomnożyć liczby rzeczywiste. Wszystko to pomoże nam sformułować następujące właściwości dla stopnia z naturalnym wskaźnikiem:

Definicja 1

1. Główna właściwość stopnia: a m a n = a m + n

Można uogólnić do postaci: a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k .

2. Własność ilorazowa dla potęg o tej samej podstawie: a m: a n = a m − n

3. Właściwość stopnia produktu: (a b) n = a n b n

Równość można rozszerzyć do: (a 1 a 2 … a k) n = a 1 n a 2 n … a k n

4. Własność stopnia naturalnego: (a: b) n = a n: b n

5. Podnosimy potęgę do potęgi: (a m) n = a m n ,

Można uogólnić do: (((a n 1) n 2) …) n k = a n 1 n 2 … n k

6. Porównaj stopień z zerem:

• jeśli a > 0, to dla dowolnego naturalnego n, a n będzie większe od zera;
• przy równym 0 n będzie również równe zero;
• dla< 0 и таком показателе степени, который будет четным числом 2 · m , a 2 · m будет больше нуля;
• dla< 0 и таком показателе степени, который будет нечетным числом 2 · m − 1 , a 2 · m − 1 будет меньше нуля.

7. Równość a n< b n будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.

8. Nierówność a m > a n będzie prawdziwa pod warunkiem, że m i n są liczbami naturalnymi, m jest większe od n, a a jest większe od zera i nie mniejsze niż jeden.

W rezultacie otrzymaliśmy kilka równości; jeśli spełnisz wszystkie warunki wskazane powyżej, będą one identyczne. Dla każdej z równości, na przykład dla właściwości głównej, możesz zamienić prawą i lewą część: a m · a n = a m + n - to samo, co a m + n = a m · a n . W tej formie jest często używany przy upraszczaniu wyrażeń.

1. Zacznijmy od głównej własności stopnia: równość a m · a n = a m + n będzie prawdziwa dla każdego naturalnego mi n i rzeczywistego a . Jak udowodnić to stwierdzenie?

Podstawowa definicja potęg z naturalnymi wykładnikami pozwoli nam zamienić równość na iloczyn czynników. Dostaniemy taki wpis:

Można to skrócić do (przypomnij sobie podstawowe własności mnożenia). W rezultacie otrzymaliśmy stopień liczby a z wykładnikiem naturalnym m + n. Zatem a m + n , co oznacza, że ​​udowodniono główną właściwość stopnia.

Przeanalizujmy konkretny przykład potwierdzając to.

Przykład 1

Mamy więc dwie potęgi o podstawie 2. Ich naturalne wskaźniki to odpowiednio 2 i 3. Otrzymaliśmy równość: 2 2 2 3 = 2 2 + 3 = 2 5 Obliczmy wartości, aby sprawdzić poprawność tej równości.

Zrealizujemy niezbędne operacje matematyczne: 2 2 2 3 = (2 2) (2 2 2) = 4 8 = 32 i 2 5 = 2 2 2 2 2 = 32

W rezultacie otrzymaliśmy: 2 2 2 3 = 2 5 . Nieruchomość została sprawdzona.

Ze względu na własności mnożenia możemy uogólnić własność formułując ją jako trzy i jeszcze potęgi, których wykładniki są liczbami naturalnymi i których podstawy są takie same. Jeśli liczbę liczb naturalnych n 1, n 2 itd. oznaczymy literą k, otrzymamy poprawną równość:

a n 1 a n 2 … a n k = a n 1 + n 2 + … + n k .

Przykład 2

2. Następnie musimy udowodnić następującą własność, która nazywa się własnością ilorazu i jest nieodłączna dla potęg o tych samych podstawach: jest to równość a m: a n = a m − n , która jest ważna dla każdego naturalnego m i n (i m jest większa niż n)) i dowolną niezerową rzeczywistą a .

Na początek wyjaśnijmy, co dokładnie oznaczają warunki wymienione w sformułowaniu. Jeśli weźmiemy równe zero, to w końcu otrzymamy dzielenie przez zero, czego nie da się zrobić (w końcu 0 n = 0). Warunek, że liczba m musi być większa niż n, jest konieczny, abyśmy mogli pozostać w obrębie naturalnych wykładników: odejmując n od m, otrzymujemy liczbę naturalną. Jeśli warunek nie zostanie spełniony, otrzymamy liczbę ujemną lub zero i ponownie wyjdziemy poza badanie stopni za pomocą naturalnych wskaźników.

Teraz możemy przejść do dowodu. Z poprzednio badanych przywołujemy podstawowe właściwości ułamków i formułujemy równość w następujący sposób:

za m − n za n = za (m − n) + n = za m

Z tego możemy wywnioskować: a m − n a n = a m

Przypomnij sobie związek między dzieleniem a mnożeniem. Wynika z tego, że a m − n jest ilorazem potęg a m i a n . To jest dowód własności drugiego stopnia.

Przykład 3

Zastąp konkretne liczby dla jasności wskaźników i oznacz podstawę stopnia π: π 5: π 2 = π 5 − 3 = π 3

3. Następnie przeanalizujemy właściwość stopnia iloczynu: (a · b) n = a n · b n dla dowolnych rzeczywistych aib oraz naturalnych n .

Zgodnie z podstawową definicją stopnia z wykładnikiem naturalnym możemy przeformułować równość w następujący sposób:

Pamiętając o własnościach mnożenia piszemy: . Oznacza to samo co a n · b n .

Przykład 4

2 3 - 4 2 5 4 = 2 3 4 - 4 2 5 4

Jeśli mamy trzy lub więcej czynników, to ta właściwość dotyczy również tego przypadku. Wprowadzamy notację k dla liczby czynników i piszemy:

(a 1 a 2 … a k) n = a 1 n a 2 n … a k n

Przykład 5

Przy określonych liczbach otrzymujemy następującą poprawną równość: (2 (- 2 , 3) ​​​​a) 7 = 2 7 (- 2 , 3) ​​7 a

4. Następnie spróbujemy udowodnić własność ilorazu: (a: b) n = a n: b n dla dowolnej rzeczywistej aib jeśli b nie jest równe 0, a n jest liczbą naturalną.

Jako dowód możemy użyć właściwości poprzedniego stopnia. Jeśli (a: b) n b n = ((a: b) b) n = a n i (a: b) n b n = a n , to z tego wynika, że ​​(a: b) n jest ilorazem dzielenia a n przez b n .

Przykład 6

Policzmy przykład: 3 1 2: - 0 . 5 3 = 3 1 2 3: (- 0 , 5) 3

Przykład 7

Zacznijmy od razu od przykładu: (5 2) 3 = 5 2 3 = 5 6

A teraz formułujemy łańcuch równości, który udowodni nam poprawność równości:

Jeśli w przykładzie mamy stopnie stopni, to ta własność jest również dla nich prawdziwa. Jeśli mamy jakieś liczby naturalne p, q, r, s, to będzie to prawda:

a p q y s = a p q y s

Przykład 8

Dodajmy konkrety: (((5 , 2) 3) 2) 5 = (5 , 2) 3 2 5 = (5 , 2) 30

6. Inną właściwością stopni z wykładnikiem naturalnym, którą musimy udowodnić, jest właściwość porównania.

Najpierw porównajmy wykładnik z zerem. Dlaczego a n > 0 pod warunkiem, że a jest większe od 0?

Jeśli pomnożymy jedną liczbę dodatnią przez drugą, otrzymamy również liczbę dodatnią. Znając ten fakt, możemy powiedzieć, że nie zależy to od liczby czynników - wynik mnożenia dowolnej liczby liczb dodatnich jest liczbą dodatnią. A czym jest stopień, jeśli nie wynikiem mnożenia liczb? Wtedy będzie to prawda dla dowolnej potęgi a n o podstawie dodatniej i wykładniku naturalnym.

Przykład 9

3 5 > 0 , (0 , 00201) 2 > 0 i 34 9 13 51 > 0

Jest też oczywiste, że potęga o podstawie równej zero sama jest zerem. Do jakiejkolwiek potęgi, którą podniesiemy zero, pozostanie ona zerem.

Przykład 10

0 3 = 0 i 0 762 = 0

Jeśli podstawą stopnia jest liczba ujemna, dowód jest nieco bardziej skomplikowany, ponieważ pojęcie parzystego / nieparzystego wykładnika staje się ważne. Zacznijmy od przypadku, gdy wykładnik jest parzysty i oznaczmy go przez 2 · m , gdzie m jest liczbą naturalną.

Pamiętajmy, jak poprawnie pomnożyć liczby ujemne: iloczyn a · a jest równy iloczynowi modułów, a więc będzie liczbą dodatnią. Następnie a stopień a 2 · m są również dodatnie.

Przykład 11

Na przykład (- 6) 4 > 0 , (-2 , 2) 12 > 0 i - 2 9 6 > 0

Co jeśli wykładnik o podstawie ujemnej jest liczbą nieparzystą? Oznaczmy to 2 · m − 1 .

Następnie

Wszystkie iloczyny a · a , zgodnie z właściwościami mnożenia, są dodatnie, podobnie jak ich iloczyn. Ale jeśli pomnożymy ją przez jedyną pozostałą liczbę a , to wynik końcowy będzie ujemny.

Wtedy otrzymujemy: (− 5) 3< 0 , (− 0 , 003) 17 < 0 и - 1 1 102 9 < 0

Jak to udowodnić?

jakiś< b n – неравенство, представляющее собой произведение левых и правых частей nверных неравенств a < b . Вспомним основные свойства неравенств справедливо и a n < b n .

Przykład 12

Na przykład nierówności są prawdziwe: 3 7< (2 , 2) 7 и 3 5 11 124 > (0 , 75) 124

8. Pozostaje nam udowodnić ostatnią właściwość: jeśli mamy dwa stopnie, których podstawy są takie same i dodatnie, a wykładniki są liczbami naturalnymi, to jeden z nich jest większy, którego wykładnik jest mniejszy; i dwóch stopni z naturalnymi wskaźnikami i tymi samymi podstawami większymi niż jeden, stopień jest większy, którego wskaźnik jest większy.

Udowodnijmy te twierdzenia.

Najpierw musimy upewnić się, że m< a n при условии, что m больше, чем n , и а больше 0 , но меньше 1 .Теперь сравним с нулем разность a m − a n

Bierzemy n z nawiasów, po czym nasza różnica przyjmie postać a n · (am − n − 1) . Jego wynik będzie ujemny (ponieważ wynik pomnożenia liczby dodatniej przez ujemną jest ujemny). Rzeczywiście, zgodnie z warunkami początkowymi, m − n > 0, wtedy a m − n − 1 jest ujemne, a pierwszy czynnik jest dodatni, jak każda siła naturalna o dodatniej podstawie.

Okazało się, że a m − a n< 0 и a m < a n . Свойство доказано.

Pozostaje udowodnić drugą część sformułowanego powyżej stwierdzenia: a m > a jest prawdziwe dla m > n oraz a > 1 . Wskazujemy różnicę i bierzemy n z nawiasów: (a m - n - 1) Potęga n z większą niż jeden da wynik pozytywny; a sama różnica również okaże się dodatnia ze względu na warunki początkowe, a dla a > 1 stopień m − n jest większy niż jeden. Okazuje się, że a m − a n > 0 i a m > a n , co musieliśmy udowodnić.

Przykład 13

Przykład z konkretnymi liczbami: 3 7 > 3 2

Podstawowe własności stopni z wykładnikami całkowitymi

Dla stopni z dodatnimi wykładnikami całkowitymi własności będą podobne, ponieważ dodatnie liczby całkowite są naturalne, co oznacza, że ​​wszystkie udowodnione powyżej równości są również dla nich ważne. Nadają się również do przypadków, w których wykładniki są ujemne lub równe zeru (pod warunkiem, że podstawa samego stopnia jest niezerowa).

Zatem własności potęg są takie same dla dowolnych podstaw a i b (pod warunkiem, że liczby te są rzeczywiste i nie są równe 0) oraz dowolnych wykładników m i n (pod warunkiem, że są to liczby całkowite). Piszemy je krótko w postaci formuł:

Definicja 2

1. za m za n = za m + n

2. a m: a n = a m − n

3. (a b) n = a n b n

4. (a: b) n = a n: b n

5. (am) n = a m n

6. n< b n и a − n >b − n z dodatnią liczbą całkowitą n , dodatnie a i b , a< b

7 rano< a n , при условии целых m и n , m >n i 0< a < 1 , при a >1 za m > za za .

Jeżeli podstawa stopnia jest równa zero, to wpisy a m i n mają sens tylko w przypadku naturalnych i dodatnich m i n. W rezultacie stwierdzamy, że powyższe formuły są również odpowiednie dla przypadków o stopniu o podstawie zerowej, jeśli wszystkie inne warunki są spełnione.

Dowody tych właściwości w tym przypadku są proste. Będziemy musieli pamiętać, czym jest stopień z wykładnikiem naturalnym i całkowitym, a także właściwości akcji z liczbami rzeczywistymi.

Przeanalizujmy własność stopnia w stopniu i udowodnijmy, że dotyczy to zarówno liczb całkowitych dodatnich, jak i niedodatnich. Zaczynamy od udowodnienia równości (a p) q = a p q , (a − p) q = a (− p) q , (a p) − q = a p (− q) i (a − p) − q = a (− p) (-q)

Warunki: p = 0 lub liczba naturalna; q - podobnie.

Jeśli wartości p i q są większe od 0, otrzymujemy (a p) q = a p · q . Już wcześniej udowodniliśmy podobną równość. Jeżeli p = 0 to:

(a 0) q = 1 q = 1 a 0 q = a 0 = 1

Dlatego (a 0) q = a 0 q

Dla q = 0 wszystko jest dokładnie takie samo:

(a p) 0 = 1 za p 0 = za 0 = 1

Wynik: (a p) 0 = a p 0 .

Jeśli oba wskaźniki mają wartość zero, to (a 0) 0 = 1 0 = 1 i a 0 0 = a 0 = 1, a następnie (a 0) 0 = a 0 0 .

Przypomnij sobie własność ilorazu w potędze udowodnionej powyżej i napisz:

1 za p q = 1 q za p q

Jeśli 1 p = 1 1 … 1 = 1 i a p q = a p q , wtedy 1 q a p q = 1 a p q

Notację tę możemy przekształcić dzięki podstawowym regułom mnożenia na a (− p) · q .

Również: a p - q = 1 (a p) q = 1 a p q = a - (p q) = a p (- q) .

AND (a - p) - q = 1 a p - q = (a p) q = a p q = a (- p) (- q)

Pozostałe właściwości stopnia można udowodnić w podobny sposób, przekształcając istniejące nierówności. Nie będziemy się nad tym szczegółowo rozwodzić, wskażemy tylko trudne punkty.

Dowód przedostatniej własności: przypomnijmy, że a − n > b − n jest prawdziwe dla dowolnych ujemnych wartości całkowitych n oraz dowolnych dodatnich a i b, pod warunkiem, że a jest mniejsze niż b .

Wówczas nierówność można przekształcić w następujący sposób:

1 za n > 1 b n

Piszemy prawą i lewą część jako różnicę i wykonujemy niezbędne przekształcenia:

1 a n - 1 b n = b n - a n a n b n

Przypomnijmy, że w warunku a jest mniejsze niż b , to zgodnie z definicją stopnia z naturalnym wskaźnikiem: - a n< b n , в итоге: b n − a n > 0 .

a n · b n kończy się liczbą dodatnią, ponieważ jej czynniki są dodatnie. W rezultacie mamy ułamek b n - a n a n · b n , co ostatecznie daje również wynik dodatni. Stąd 1 a n > 1 b n skąd a − n > b − n , co musieliśmy udowodnić.

Ostatnia własność stopni z wykładnikami całkowitymi dowodzi się podobnie do własności stopni z wykładnikami naturalnymi.

Podstawowe własności stopni z wykładnikami wymiernymi

W poprzednich artykułach omawialiśmy, czym jest stopień z wykładnikiem wymiernym (ułamkowym). Ich właściwości są takie same jak w przypadku stopni z wykładnikami całkowitymi. Napiszmy:

Definicja 3

1. a m 1 n 1 a m 2 n 2 = a m 1 n 1 + m 2 n 2 dla a > 0 i jeśli m 1 n 1 > 0 i m 2 n 2 > 0, to dla a ≥ 0 z tą samą podstawą).

2. a m 1 n 1: b m 2 n 2 = a m 1 n 1 - m 2 n 2 jeśli a > 0 (właściwość ilorazowa).

3. abmn = amnbmn dla a > 0 i b > 0, a jeśli m 1 n 1 > 0 i m 2 n 2 > 0, to dla a ≥ 0 i (lub) b ≥ 0 (właściwość produktu w stopniu ułamkowym).

4. a: b m n \u003d a m n: b m n dla a > 0 i b > 0, a jeśli m n > 0, to dla a ≥ 0 i b > 0 (właściwość ilorazu do potęgi ułamkowej).

5. a m 1 n 1 m 2 n 2 \u003d am 1 n 1 m 2 n 2 dla a > 0, a jeśli m 1 n 1 > 0 i m 2 n 2 > 0, to dla a ≥ 0 (właściwość stopnia w stopni).

6.ap< b p при условии любых положительных a и b , a < b и рациональном p при p >0; Jeżeli p< 0 - a p >b p (właściwość porównywania stopni z równymi wykładnikami wymiernymi).

7.ap< a q при условии рациональных чисел p и q , p >q w 0< a < 1 ; если a >0 – a p > a q

Aby udowodnić te przepisy, musimy pamiętać, co to jest stopień z wykładnikiem ułamkowym, jakie są właściwości pierwiastka arytmetycznego n-tego stopnia, a jakie są właściwości stopnia z wykładnikiem całkowitym. Przyjrzyjmy się każdej nieruchomości.

Zgodnie z tym, czym jest stopień z wykładnikiem ułamkowym, otrzymujemy:

jestem 1 n 1 \u003d jestem 1 n 1 i jestem 2 n 2 \u003d jestem 2 n 2, zatem jestem 1 n 1 jestem 2 n 2 \u003d jestem 1 n 1 jestem 2 n 2

Właściwości korzenia pozwolą nam wyprowadzić równości:

za m 1 m 2 za 1 za 2 za m 2 za za 1 za 2 za 1 = za za 1 za 2 za za m 2 za 1 z 1 za 2

Z tego otrzymujemy: a m 1 n 2 a m 2 n 1 n 1 n 2 = a m 1 n 2 + m 2 n 1 n 1 n 2

Przekształćmy:

za m 1 w 2 za m 2 w 1 w 1 w 2 = za m 1 w 2 + m 2 w 1 w 1 w 2

Wykładnik można zapisać jako:

m 1 n 2 + m 2 n 1 n 1 n 2 = m 1 n 2 n 1 n 2 + m 2 n 1 n 1 n 2 = m 1 n 1 + m 2 n 2

To jest dowód. Druga właściwość jest udowadniana dokładnie w ten sam sposób. Zapiszmy łańcuch równości:

a m 1 n 1: a m 2 n 2 = a m 1 n 1: a m 2 n 2 = a m 1 n 2: a m 2 n 1 n 1 n 2 = = a m 1 n 2 - m 2 n 1 n 1 n 2 = a m 1 n 2 - m 2 n 1 n 1 n 2 = jestem 1 n 2 n 1 n 2 - m 2 n 1 n 1 n 2 = mam 1 n 1 - m 2 n 2

Dowody pozostałych równości:

abmn = (ab)mn=ambmn=amnbmn=amnbmn; (a: b) m n = (a: b) m n = a m: b m n = = a m n: b m n = a m n: b m n ; a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = = a m 1 m 2 n 1 n 2 = a m 1 m 2 n 1 n 2 = = a m 1 m 2 n 2 n 1 = jestem 1 m 2 n 2 n 1 = jestem 1 n 1 m 2 n 2

Następna właściwość: udowodnijmy, że dla dowolnych wartości a i b większych od 0 , jeśli a jest mniejsze od b , zostanie wykonane p< b p , а для p больше 0 - a p >bp

Reprezentujmy liczbę wymierną p jako m n . W tym przypadku m jest liczbą całkowitą, n jest liczbą naturalną. Wtedy warunki p< 0 и p >0 zostanie rozszerzone do m< 0 и m >0 . Dla m > 0 i a< b имеем (согласно свойству степени с целым положительным показателем), что должно выполняться неравенство a m < b m .

Używamy własności pierwiastków i wyprowadzamy: a m n< b m n

Biorąc pod uwagę dodatniość wartości a i b przepisujemy nierówność jako a m n< b m n . Оно эквивалентно a p < b p .

W ten sam sposób dla m< 0 имеем a a m >b m , otrzymujemy a m n > b m n więc a m n > b m n i a p > b p .

Pozostaje nam udowodnić ostatnią właściwość. Udowodnijmy, że dla liczb wymiernych p i q , p > q dla 0< a < 1 a p < a q , а при a >0 byłoby prawdziwe a p > a q .

Liczby wymierne p i q można sprowadzić do wspólnego mianownika i uzyskać ułamki m 1 n i m 2 n

Tutaj m 1 i m 2 są liczbami całkowitymi, a n jest liczbą naturalną. Jeżeli p > q, to ​​m 1 > m 2 (uwzględniając zasadę porównywania ułamków). Następnie o 0< a < 1 будет верно a m 1 < a m 2 , а при a >1 – nierówność a 1 m > a 2 m .

Można je przepisać w następującej formie:

a m 1 n< a m 2 n a m 1 n >a m 2 n

Następnie możesz dokonać przekształceń i uzyskać w rezultacie:

a m 1 n< a m 2 n a m 1 n >a m 2 n

Podsumowując: dla p > q i 0< a < 1 верно a p < a q , а при a >0 – a p > a q .

Podstawowe własności stopni z niewymiernymi wykładnikami

Wszystkie opisane powyżej własności, jakie posiada stopień z wymiernymi wykładnikami, można rozszerzyć do takiego stopnia. Wynika to z samej jego definicji, którą podaliśmy w jednym z poprzednich artykułów. Sformułujmy pokrótce te własności (warunki: a > 0 , b > 0 , wskaźniki p i q są liczbami niewymiernymi):

Definicja 4

1. a p a q = a p + q

2. a p: a q = a p − q

3. (a b) p = a p b p

4. (a: b) p = a p: b p

5. (a p) q = a p q

6.ap< b p верно при любых положительных a и b , если a < b и p – иррациональное число больше 0 ; если p меньше 0 , то a p >bp

7.ap< a q верно, если p и q – иррациональные числа, p < q , 0 < a < 1 ; если a >0 , potem a p > a q .

Zatem wszystkie potęgi, których wykładniki p i q są liczbami rzeczywistymi, pod warunkiem, że a > 0, mają te same własności.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Jak mnożyć moce? Jakie potęgi można mnożyć, a jakie nie? Jak pomnożyć liczbę przez potęgę?

W algebrze można znaleźć iloczyn potęgowania w dwóch przypadkach:

1) jeżeli stopnie mają tę samą podstawę;

2) jeżeli stopnie mają te same wskaźniki.

Mnożąc potęgi o tej samej podstawie, podstawa musi pozostać taka sama, a wykładniki muszą zostać dodane:

Mnożąc stopnie za pomocą tych samych wskaźników, całkowity wskaźnik można wyjąć z nawiasów:

Zastanów się, jak pomnożyć moce na konkretnych przykładach.

Jednostka w wykładniku nie jest zapisywana, ale mnożąc stopnie, uwzględniają:

Podczas mnożenia liczba stopni może być dowolna. Należy pamiętać, że nie można napisać znaku mnożenia przed literą:

W wyrażeniach potęgowanie jest wykonywane jako pierwsze.

Jeśli potrzebujesz pomnożyć liczbę przez potęgę, musisz najpierw wykonać potęgowanie, a dopiero potem - mnożenie:

www.algebraclass.ru

Dodawanie, odejmowanie, mnożenie i dzielenie potęgi

Dodawanie i odejmowanie potęg

Oczywiście liczby z potęgami można dodawać jak inne wielkości , dodając je jeden po drugim wraz z ich znakami.

Zatem suma a 3 i b 2 to a 3 + b 2 .
Suma a 3 - b n i h 5 -d 4 to a 3 - b n + h 5 - d 4.

Szanse te same moce tych samych zmiennych można dodawać lub odejmować.

Zatem suma 2a 2 i 3a 2 to 5a 2 .

Jest też oczywiste, że jeśli weźmiemy dwa kwadraty a, lub trzy kwadraty a, lub pięć kwadratów a.

Ale stopnie różne zmienne oraz różne stopnie identyczne zmienne, należy dodać, dodając je do ich znaków.

Zatem suma a 2 i a 3 jest sumą a 2 + a 3 .

Jest oczywiste, że kwadrat a i sześcian a nie jest ani dwukrotnością kwadratu a, ale dwukrotnością sześcianu a.

Suma a 3 b n i 3a 5 b 6 to a 3 b n + 3a 5 b 6 .

Odejmowanie uprawnienia są wykonywane w taki sam sposób, jak dodawanie, z tym wyjątkiem, że znaki oddzielenia muszą być odpowiednio zmienione.

Lub:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 - 4h 2 b 6 \u003d -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6

Mnożenie potęgi

Liczby z potęgami można mnożyć, podobnie jak inne wielkości, pisząc je jedna po drugiej, z lub bez znaku mnożenia między nimi.

Tak więc wynik pomnożenia a 3 przez b 2 to a 3 b 2 lub aaabb.

Lub:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 x y 2
a 2 b 3 r 2 ⋅ a 3 b 2 r = a 2 b 3 r 2 za 3 b 2 r

Wynik w ostatnim przykładzie można uporządkować, dodając te same zmienne.
Wyrażenie przyjmie postać: a 5 b 5 y 3 .

Porównując kilka liczb (zmiennych) z potęgami, widzimy, że jeśli pomnoży się dowolne dwie z nich, to otrzymamy liczbę (zmienną) o potędze równej suma stopnie terminów.

A więc a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Tutaj 5 jest potęgą wyniku mnożenia, równą 2 + 3, sumą potęg wyrazów.

A więc n .a m = a m+n .

Dla n , a jest brane jako czynnik tyle razy, ile jest potęgi n;

A m , przyjmuje się jako czynnik tyle razy, ile stopni m jest równe;

Dlatego, potęgi o tych samych podstawach można pomnożyć przez dodanie wykładników.

A więc a 2 .a 6 = a 2+6 = a 8 . Oraz x 3 .x 2 .x = x 3+2+1 = x 6 .

Lub:
4a n ⋅ 2a n = 8a 2n
b 2 r 3 ⋅ b 4 r = b 6 r 4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1

Pomnóż (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Odpowiedź: x 4 - y 4.
Pomnóż (x 3 + x - 5) ⋅ (2x 3 + x + 1).

Ta zasada odnosi się również do liczb, których wykładniki wynoszą − negatywny.

1. A więc a -2 .a -3 = a -5 . Można to zapisać jako (1/aa).(1/aaa) = 1/aaaaa.

2. y-n .y-m = y-n-m .

3. a-n .a m = a m-n .

Jeśli a + b pomnożymy przez a - b, wynikiem będzie a 2 - b 2: czyli

Wynik pomnożenia sumy lub różnicy dwóch liczb jest równy sumie lub różnicy ich kwadratów.

Jeśli suma i różnica dwóch liczb podniesiona do kwadrat, wynik będzie równy sumie lub różnicy tych liczb w czwarty stopień.

Tak więc (a - y).(a + y) = a 2 - y 2 .
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4 .
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8 .

Podział władz

Liczby z potęgami można dzielić tak jak inne liczby, odejmując od dzielnika lub umieszczając je w postaci ułamka.

Więc a 3 b 2 podzielone przez b 2 to a 3 .

Zapisanie 5 podzielonej przez 3 wygląda jak $\frac $. Ale to jest równe 2 . W serii liczb
za +4 , za +3 ​​, za +2 , za +1 , za 0 , za -1 , za -2 , za -3 , za -4 .
dowolną liczbę można podzielić przez drugą, a wykładnik będzie równy różnica wskaźniki liczb podzielnych.

Dzieląc potęgi o tej samej podstawie, ich wykładniki są odejmowane..

Tak więc y 3: y 2 = y 3-2 = y 1 . Oznacza to, że $\frac = y$.

A n+1:a = a n+1-1 = a n . Czyli $\frac = a^n$.

Lub:
y2m: ym = ym
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b + y) n-3

Zasada obowiązuje również dla liczb z negatywny wartości stopni.
Wynik dzielenia -5 przez -3 daje -2 .
Również $\frac: \frac = \frac .\frac = \frac = \frac $.

h 2:h -1 = h 2+1 = h 3 lub $h^2:\frac = h^2.\frac = h^3$

Konieczne jest bardzo dobre opanowanie mnożenia i dzielenia potęg, ponieważ takie operacje są bardzo szeroko stosowane w algebrze.

Przykłady rozwiązywania przykładów z ułamkami zawierającymi liczby z potęgami

1. Zmniejsz wykładniki w $\frac $ Odpowiedź: $\frac $.

2. Zmniejsz wykładniki w $\frac$. Odpowiedź: $\frac $ lub 2x.

3. Zmniejsz wykładniki 2/a 3 i a-3/a -4 i doprowadź do wspólnego mianownika.
a 2 .a -4 to pierwszy licznik -2.
a 3 .a -3 to 0 = 1, drugi licznik.
a 3 .a -4 to -1 , wspólny licznik.
Po uproszczeniu: a -2 /a -1 i 1/a -1 .

4. Zmniejsz wykładniki 2a 4 /5a 3 i 2 /a 4 i doprowadź do wspólnego mianownika.
Odpowiedź: 2a 3 / 5a 7 i 5a 5 / 5a 7 lub 2a 3 / 5a 2 i 5/5a 2.

5. Pomnóż (a 3 + b)/b 4 przez (a - b)/3.

6. Pomnóż (a 5 + 1)/x 2 przez (b 2 - 1)/(x + a).

7. Pomnóż b 4 /a -2 przez h -3 /x i a n /y -3 .

8. Podziel 4 /y 3 przez 3 /y 2 . Odpowiedź: a/y.

właściwości stopnia

Przypominamy, że w tej lekcji rozumiemy właściwości stopnia z naturalnymi wskaźnikami i zerem. Stopnie z wymiernymi wskaźnikami i ich właściwości zostaną omówione na lekcjach dla klasy 8.

Wykładnik z wykładnikiem naturalnym ma kilka ważnych właściwości, które pozwalają uprościć obliczenia w przykładowych wykładnikach.

Właściwość #1
Iloczyn uprawnień

Podczas mnożenia potęg przy tej samej podstawie podstawa pozostaje niezmieniona, a wykładniki są dodawane.

a m a n \u003d a m + n, gdzie „a” to dowolna liczba, a „m”, „n” to dowolne liczby naturalne.

Ta właściwość potęgi wpływa również na iloczyn trzech lub więcej potęg.

Należy pamiętać, że we wskazanej właściwości chodziło tylko o mnożenie potęg przy tych samych podstawach.. Nie dotyczy ich dodawania.

Nie możesz zastąpić sumy (3 3 + 3 2) przez 3 5 . Jest to zrozumiałe, jeśli
obliczyć (3 3 + 3 2) = (27 + 9) = 36 i 3 5 = 243

Właściwość #2
Stopnie prywatne

Podczas dzielenia potęgi za pomocą tej samej podstawy podstawa pozostaje niezmieniona, a wykładnik dzielnika jest odejmowany od wykładnika dywidendy.

Oblicz.

11 3 - 2 4 2 - 1 = 11 4 = 44
Przykład. Rozwiązać równanie. Korzystamy z własności częściowych stopni.
3 8: t = 3 4

Odpowiedź: t = 3 4 = 81

Korzystając z właściwości nr 1 i nr 2, możesz łatwo uprościć wyrażenia i wykonać obliczenia.

Przykład. Uprość wyrażenie.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5

Przykład. Znajdź wartość wyrażenia za pomocą właściwości stopnia.

2 11 − 5 = 2 6 = 64

Należy pamiętać, że właściwość 2 dotyczyła wyłącznie podziału kompetencji za pomocą tych samych zasad.

Nie możesz zastąpić różnicy (4 3 -4 2) przez 4 1 . Jest to zrozumiałe, jeśli obliczysz (4 3 −4 2) = (64 − 16) = 48 i 4 1 = 4

Właściwość #3
Potęgowanie

Przy podnoszeniu potęgi do potęgi podstawa potęgi pozostaje niezmieniona, a wykładniki są mnożone.

(a n) m \u003d a n m, gdzie „a” to dowolna liczba, a „m”, „n” to dowolne liczby naturalne.

Należy pamiętać, że właściwość nr 4, podobnie jak inne właściwości stopni, jest również stosowana w odwrotnej kolejności.

(a n b n)= (a b) n

Oznacza to, że aby pomnożyć stopnie przy tych samych wykładnikach, można pomnożyć podstawy i pozostawić wykładnik bez zmian.

W bardziej złożonych przykładach mogą wystąpić przypadki, w których mnożenie i dzielenie musi być wykonane na potęgach o różnych podstawach i różnych wykładnikach. W takim przypadku radzimy wykonać następujące czynności.

Na przykład 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216

Przykład potęgowania ułamka dziesiętnego.

4 21 (−0.25) 20 = 4 4 20 (−0.25) 20 = 4 (4 (−0.25)) 20 = 4 (−1) 20 = 4 1 = cztery

Właściwości 5
Potęga ilorazu (ułamki)

Aby podnieść iloraz do potęgi, możesz podnieść dzielną i dzielnik oddzielnie do tej potęgi i podzielić pierwszy wynik przez drugi.

(a: b) n \u003d a n: b n, gdzie „a”, „b” to dowolne liczby wymierne, b ≠ 0, n to dowolna liczba naturalna.

Przypominamy, że iloraz można przedstawić jako ułamek. Dlatego bardziej szczegółowo zajmiemy się tematem podniesienia ułamka do potęgi na następnej stronie.

Stopnie i korzenie

Operacje z potęgami i korzeniami. Stopień z negatywem ,

zero i ułamek wskaźnik. O wyrażeniach, które nie mają sensu.

Operacje ze stopniami.

1. Mnożąc moce o tej samej podstawie, ich wskaźniki sumują się:

jestem · a n = a m + n .

2. Dzieląc stopnie o tej samej podstawie, ich wskaźniki odejmowane .

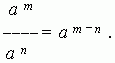
3. Stopień iloczynu dwóch lub więcej czynników jest równy iloczynowi stopni tych czynników.

4. Stopień stosunku (ułamka) jest równy stosunkowi stopni dywidendy (licznik) i dzielnika (mianownik):

(a/b) n = a n / b n .

5. Podnosząc stopień do potęgi, ich wskaźniki są mnożone:

Wszystkie powyższe formuły są odczytywane i wykonywane w obu kierunkach od lewej do prawej i odwrotnie.

PRZYKŁAD (2 3 5 / 15)² = 2 ² 3 ² 5 ² / 15 ² = 900 / 225 = 4 .

Operacje z korzeniami. We wszystkich poniższych formułach symbol oznacza pierwiastek arytmetyczny(radykalna ekspresja jest pozytywna).

1. Korzeń iloczynu kilku czynników jest równy produktowi korzenie tych czynników:

2. Pierwiastek stosunku jest równy stosunkowi pierwiastków dywidendy i dzielnika:

3. Podnosząc korzeń do potęgi, wystarczy wznieść się do tej potęgi numer główny:

4. Jeśli zwiększysz stopień pierwiastka o m razy i jednocześnie podniesiesz liczbę pierwiastka do m -tego stopnia, wartość pierwiastka nie zmieni się:

5. Jeśli zmniejszysz stopień pierwiastka o m razy i jednocześnie wyodrębnisz pierwiastek m-tego stopnia z liczby radykalnej, wartość pierwiastka nie zmieni się:

Rozszerzenie pojęcia stopnia. Do tej pory rozważaliśmy stopnie naukowe wyłącznie z naturalnym wskaźnikiem; ale operacje z mocami i korzeniami mogą również prowadzić do negatywny, zero oraz frakcyjny wskaźniki. Wszystkie te wykładniki wymagają dodatkowej definicji.

Stopień z ujemnym wykładnikiem. Stopień pewnej liczby z wykładnikiem ujemnym (całkowitym) jest definiowany jako stopień podzielony przez stopień tej samej liczby z wykładnikiem równym wartości bezwzględnej wykładnika ujemnego:

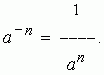
Teraz formuła jestem : jakiś = m-n może służyć nie tylko do m, więcej niż n, ale także w m, mniej niż n .

PRZYKŁAD a 4: a 7 = a 4 — 7 = a — 3 .

Jeśli chcemy formuły jestem : jakiś = jestem — n było uczciwe w m = n, potrzebujemy definicji stopnia zerowego.

Stopień z wykładnikiem zerowym. Stopień dowolnej liczby niezerowej z wykładnikiem zerowym wynosi 1.

PRZYKŁADY. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.

Stopień z wykładnikiem ułamkowym. Aby podnieść liczbę rzeczywistą a do potęgi m / n, musisz wydobyć pierwiastek n-tego stopnia z m-tej potęgi tej liczby a:

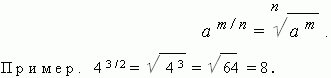
O wyrażeniach, które nie mają sensu. Jest kilka takich wyrażeń.

gdzie a ≠ 0 , nie istnieje.

Rzeczywiście, jeśli założymy, że x jest pewną liczbą, to zgodnie z definicją operacji dzielenia mamy: a = 0· x, tj. a= 0, co jest sprzeczne z warunkiem: a ≠ 0

— Jakikolwiek numer.

Rzeczywiście, jeśli założymy, że to wyrażenie jest równe pewnej liczbie x, to zgodnie z definicją operacji dzielenia mamy: 0 = 0 x. Ale ta równość trwa dowolna liczba x, co miało zostać udowodnione.

0 0 — Jakikolwiek numer.

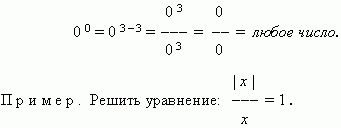
Rozwiązanie Rozważ trzy główne przypadki:

1) x = 0 – ta wartość nie spełnia tego równania

2) kiedy x> 0 otrzymujemy: x / x= 1, tj. 1 = 1, skąd wynika,

Co x- Jakikolwiek numer; ale biorąc to pod uwagę

nasza sprawa x> 0 , odpowiedź brzmi x > 0 ;

Zasady mnożenia potęg z różnymi podstawami

STOPIEŃ Z WSKAŹNIKIEM RACJONALNOŚCI,

FUNKCJA ZASILANIA IV

§ 69. Mnożenie i podział władz przy tych samych podstawach”

Twierdzenie 1. Aby pomnożyć potęgi o tych samych podstawach, wystarczy dodać wykładniki i pozostawić podstawę bez zmian, czyli

Dowód. Z definicji stopnia

2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.

Rozważaliśmy iloczyn dwóch sił. W rzeczywistości udowodniona własność jest prawdziwa dla dowolnej liczby potęg o tych samych podstawach.

Twierdzenie 2. Aby podzielić uprawnienia o tych samych podstawach, gdy wskaźnik dzielnika jest większy niż wskaźnik dzielnika, wystarczy odjąć wskaźnik dzielnika od wskaźnika dywidendy i pozostawić tę samą podstawę, czyli w t > n

(a =/= 0)

Dowód. Przypomnijmy, że iloraz dzielenia jednej liczby przez drugą jest liczbą, która po pomnożeniu przez dzielnik daje dywidendę. Dlatego udowodnij wzór , gdzie a =/= 0, to jak udowodnienie wzoru

Jeśli t > n , to liczba t - p będzie naturalny; zatem przez twierdzenie 1

Twierdzenie 2 jest udowodnione.

Zauważ, że formuła

udowodnione przez nas tylko przy założeniu, że t > n . Dlatego z tego, co zostało udowodnione, nie można jeszcze wyciągnąć na przykład następujących wniosków:

Ponadto nie rozważaliśmy jeszcze stopni z ujemnymi wykładnikami i nie wiemy jeszcze, jakie znaczenie można nadać wyrażeniu 3 - 2 .

Twierdzenie 3. Aby podnieść potęgę do potęgi, wystarczy pomnożyć wykładniki, pozostawiając taką samą podstawę wykładnika, to znaczy

Dowód. Korzystając z definicji stopnia i Twierdzenia 1 z tego rozdziału, otrzymujemy:

co było do okazania

Na przykład (2 3) 2 = 2 6 = 64;

518 (ust.) Określ X z równań:

1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;

2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .

519. (Dostosowany) Uprość:

520. (Dostosowany) Uprość:

521. Przedstaw te wyrażenia jako stopnie o tych samych podstawach:

1) 32 i 64; 3) 85 i 163; 5) 4 100 i 32 50;

2) -1000 i 100; 4) -27 i -243; 6) 81 75 8 200 i 3 600 4 150.