Σπίτι

Φράκταλ Xaos. Φράκταλ στη βιολογία. Χρυσή αναλογία, φράκταλ και χάος

Διδάκτωρ Φυσικών και Μαθηματικών Επιστημών A. DMITRIEV, κορυφαίος ερευνητής στο Ινστιτούτο Ραδιομηχανικής και Ηλεκτρονικής της Ρωσικής Ακαδημίας Επιστημών (Μόσχα).

Το δυναμικό (ντετερμινιστικό) χάος και τα φράκταλ είναι έννοιες που εισήλθαν στην επιστημονική εικόνα του κόσμου σχετικά πρόσφατα, μόλις στο τελευταίο τέταρτο του εικοστού αιώνα. Έκτοτε, το ενδιαφέρον για αυτούς δεν έχει ξεθωριάσει όχι μόνο μεταξύ των ειδικών - φυσικών, μαθηματικών, βιολόγων κ.λπ., αλλά και μεταξύ ανθρώπων μακριά από την επιστήμη. Η έρευνα που σχετίζεται με τα φράκταλ και το ντετερμινιστικό χάος αλλάζει πολλές από τις συνήθεις ιδέες για τον κόσμο γύρω μας. Και όχι για τον κόσμο των μικροαντικειμένων, όπου το ανθρώπινο μάτι είναι ανίσχυρο χωρίς ειδικό εξοπλισμό, και όχι για φαινόμενα σε κοσμική κλίμακα, αλλά για τα πιο συνηθισμένα αντικείμενα: σύννεφα, ποτάμια, δέντρα, βουνά, γρασίδι. Τα φράκταλ μας αναγκάζουν να επανεξετάσουμε τις απόψεις μας για τις γεωμετρικές ιδιότητες των φυσικών και τεχνητών αντικειμένων και το δυναμικό χάος εισάγει ριζικές αλλαγές στην κατανόηση του τρόπου συμπεριφοράς αυτών των αντικειμένων με την πάροδο του χρόνου. Οι θεωρίες που αναπτύχθηκαν με βάση αυτές τις έννοιες ανοίγουν νέες ευκαιρίες σε διάφορους τομείς της γνώσης, συμπεριλαμβανομένων των τεχνολογιών πληροφοριών και επικοινωνιών.

Επιστήμη και ζωή // Εικονογραφήσεις

Τα δέντρα, όπως και πολλά άλλα αντικείμενα στη φύση, έχουν δομή φράκταλ.

Επιστήμη και ζωή // Εικονογραφήσεις

Το πεύκο της Κριμαίας (αριστερά) και η τεχνητή δομή φράκταλ (δεξιά) είναι εκπληκτικά παρόμοια.

Απόκριση ταλαντευτικού κυκλώματος σε εξωτερικό περιοδικό σήμα: α - περιοδική απόκριση γραμμικού κυκλώματος, β - χαοτική απόκριση μη γραμμικού κυκλώματος. Ο ρόλος της μη γραμμικής χωρητικότητας εκτελείται από τη διασταύρωση p-n της διόδου ημιαγωγών.

Η κίνηση ενός δυναμικού συστήματος μπορεί να αναπαρασταθεί οπτικά με μια τροχιά στο επίπεδο φάσης, όπου οι άξονες X και Y είναι η γενικευμένη συντεταγμένη και ορμή του σωματιδίου. α - ταλαντώσεις ενός αποσβεσμένου εκκρεμούς.

Παραδείγματα συστημάτων με χάος.

Επιστήμη και ζωή // Εικονογραφήσεις

Οι κύριοι τρόποι συγχρονισμού χαοτικών συστημάτων: α - μέσω παγκόσμιων συνδέσεων: κάθε σύστημα επηρεάζει το ένα το άλλο. β - με τη βοήθεια ενός βηματοδότη, ή «βηματοδότη»: ένα από τα συστήματα ορίζει το ρυθμό για όλα τα άλλα στοιχεία.

Επιστήμη και ζωή // Εικονογραφήσεις

Ένα παράδειγμα καταγραφής πληροφοριών χρησιμοποιώντας ντετερμινιστικό χάος.

Οι υπάλληλοι του εργαστηρίου InformChaos του Ινστιτούτου Ραδιομηχανικής και Ηλεκτρονικής της Ρωσικής Ακαδημίας Επιστημών A. I. Panas και S. O. Starkov διεξάγουν ένα πείραμα για την άμεση χαοτική μετάδοση δεδομένων υψηλής ταχύτητας στην περιοχή μικροκυμάτων (παραπάνω).

Έτσι μοιάζουν οι χαοτικές ταλαντώσεις μικροκυμάτων, καθιστώντας δυνατή την αύξηση της ταχύτητας μεταφοράς πληροφοριών δεκάδες φορές σε σύγκριση με τα παραδοσιακά συστήματα.

Τι είναι ένα φράκταλ;

Τα φράκταλ είναι παντού γύρω μας, τόσο στα περιγράμματα των βουνών όσο και στην ελικοειδή γραμμή της ακτής. Μερικά από τα φράκταλ αλλάζουν συνεχώς, όπως τα κινούμενα σύννεφα ή οι φλόγες που τρεμοπαίζουν, ενώ άλλα, όπως τα δέντρα ή τα αγγειακά μας συστήματα, διατηρούν μια δομή που αποκτάται μέσω της διαδικασίας της εξέλιξης.
H. O. Peigen και P. H. Richter.

Η γεωμετρία που μελετήσαμε στο σχολείο και χρησιμοποιούμε στην καθημερινή ζωή ανάγεται στον Ευκλείδη (περίπου 300 π.Χ.). Τρίγωνα, τετράγωνα, κύκλοι, παραλληλόγραμμα, παραλληλεπίπεδα, πυραμίδες, σφαίρες, πρίσματα είναι τυπικά αντικείμενα που θεωρούνται από την κλασική γεωμετρία. Τα τεχνητά αντικείμενα συνήθως περιλαμβάνουν αυτές τις φιγούρες ή θραύσματά τους. Ωστόσο, στη φύση δεν βρίσκονται πολύ συχνά. Πράγματι, είναι, για παράδειγμα, οι ομορφιές του δάσους της ερυθρελάτης παρόμοιες με κάποιο από τα στοιχεία που αναφέρονται ή ο συνδυασμός τους; Είναι εύκολο να παρατηρήσετε ότι, σε αντίθεση με τις μορφές του Ευκλείδη, τα φυσικά αντικείμενα δεν είναι λεία, οι άκρες τους είναι σπασμένες, οδοντωτές, οι επιφάνειές τους είναι τραχιές, διαβρωμένες από ρωγμές, περάσματα και τρύπες. "Γιατί η γεωμετρία ονομάζεται συχνά ψυχρή και ξηρή; Ένας λόγος είναι η αδυναμία της να περιγράψει το σχήμα ενός σύννεφου, ενός βουνού, ενός δέντρου ή μιας αιγιαλού. Τα σύννεφα δεν είναι σφαίρες, τα βουνά δεν είναι κώνοι, οι ακτές δεν είναι κύκλοι και ο φλοιός δεν είναι ομαλή." , και οι κεραυνοί δεν ταξιδεύουν σε ευθεία γραμμή. Η φύση δεν μας δείχνει απλώς έναν υψηλότερο βαθμό, αλλά ένα εντελώς διαφορετικό επίπεδο πολυπλοκότητας", αυτές οι λέξεις ξεκινούν "The Fractal Geometry of Nature", γραμμένο από τον Benoit Mandelbrot . Ήταν αυτός που εισήγαγε για πρώτη φορά την έννοια του φράκταλ το 1975 - από τη λατινική λέξη fractus, σπασμένη πέτρα, σχισμένη και ακανόνιστη. Αποδεικνύεται ότι σχεδόν όλοι οι φυσικοί σχηματισμοί έχουν δομή φράκταλ. Τι σημαίνει? Εάν κοιτάξετε ένα φράκταλ αντικείμενο στο σύνολό του, μετά σε ένα μέρος του σε μεγέθυνση, μετά σε ένα μέρος αυτού του τμήματος κ.λπ., τότε δεν είναι δύσκολο να δείτε ότι φαίνονται το ίδιο. Τα φράκταλ είναι ίδια - το σχήμα τους αναπαράγεται σε διαφορετικές κλίμακες.

Η ανακάλυψη των φράκταλ έφερε επανάσταση όχι μόνο στη γεωμετρία, αλλά και στη φυσική, τη χημεία και τη βιολογία. Οι αλγόριθμοι φράκταλ έχουν επίσης βρει εφαρμογή σε τεχνολογίες πληροφοριών, για παράδειγμα, για τη σύνθεση τρισδιάστατων εικόνων υπολογιστή φυσικών τοπίων, για συμπίεση (συμπίεση) δεδομένων (βλ. «Science and Life» No. 4, 1994; No. 8, 12, 1995, Νο. 7, 1998). Στη συνέχεια, θα βεβαιωθούμε ότι η έννοια ενός φράκταλ σχετίζεται στενά με ένα άλλο όχι λιγότερο ενδιαφέρον φαινόμενο - το χάος στα δυναμικά συστήματα.

Ντετερμινισμός και χάος

ΧΑΟΣ (ελληνικό caos) - στην ελληνική μυθολογία, μια απεριόριστη πρωτόγονη μάζα,
από το οποίο στη συνέχεια σχηματίστηκε
όλα όσα υπάρχουν. Με μεταφορική έννοια - αταξία, σύγχυση.
Εγκυκλοπαιδεία
Κύριλλος και Μεθόδιος

Όταν μιλούν για τον ντετερμινισμό ενός συγκεκριμένου συστήματος, εννοούν ότι η συμπεριφορά του χαρακτηρίζεται από μια σαφή σχέση αιτίου-αποτελέσματος. Δηλαδή, γνωρίζοντας τις αρχικές συνθήκες και τον νόμο κίνησης του συστήματος, μπορείτε να προβλέψετε με ακρίβεια το μέλλον του. Είναι αυτή η ιδέα της κίνησης στο Σύμπαν που είναι χαρακτηριστική της κλασικής, Νευτώνειας δυναμικής. Το χάος, αντίθετα, συνεπάγεται μια άτακτη, τυχαία διαδικασία, όταν η πορεία των γεγονότων δεν μπορεί ούτε να προβλεφθεί ούτε να αναπαραχθεί. Τι είναι το ντετερμινιστικό χάος - η φαινομενικά αδύνατη ενοποίηση δύο αντίθετων εννοιών;

Ας ξεκινήσουμε με μια απλή εμπειρία. Μια μπάλα κρεμασμένη σε ένα νήμα εκτρέπεται από την κατακόρυφο και απελευθερώνεται. Εμφανίζεται δισταγμός. Εάν η μπάλα εκτρέπεται ελαφρά, τότε η κίνησή της περιγράφεται με γραμμικές εξισώσεις. Εάν η απόκλιση γίνει αρκετά μεγάλη, οι εξισώσεις δεν θα είναι πλέον γραμμικές. Τι θα αλλάξει; Στην πρώτη περίπτωση, η συχνότητα ταλάντωσης (και, κατά συνέπεια, η περίοδος) δεν εξαρτάται από τον βαθμό της αρχικής απόκλισης. Στο δεύτερο συμβαίνει μια τέτοια εξάρτηση. Ένα πλήρες ανάλογο ενός μηχανικού εκκρεμούς ως ταλαντευόμενου συστήματος είναι ένα ταλαντευόμενο κύκλωμα ή «ηλεκτρικό εκκρεμές». Στην απλούστερη περίπτωση, αποτελείται από έναν επαγωγέα, έναν πυκνωτή (χωρητικότητα) και μια αντίσταση (αντίσταση). Αν και τα τρία αυτά στοιχεία είναι γραμμικά, τότε οι ταλαντώσεις στο κύκλωμα είναι ισοδύναμες με τις ταλαντώσεις ενός γραμμικού εκκρεμούς. Αλλά εάν, για παράδειγμα, η χωρητικότητα είναι μη γραμμική, η περίοδος των ταλαντώσεων θα εξαρτηθεί από το πλάτος τους.

Η δυναμική ενός κυκλώματος ταλάντωσης καθορίζεται από δύο μεταβλητές, για παράδειγμα, το ρεύμα στο κύκλωμα και την τάση κατά μήκος του πυκνωτή. Εάν σχεδιάσουμε αυτές τις ποσότητες κατά μήκος των αξόνων X και Y, τότε κάθε κατάσταση του συστήματος θα αντιστοιχεί σε ένα συγκεκριμένο σημείο στο προκύπτον επίπεδο συντεταγμένων. Αυτό το αεροπλάνο ονομάζεται φάση. (Αντίστοιχα, εάν οριστεί το δυναμικό σύστημα nμεταβλητές, τότε αντί για δισδιάστατο επίπεδο φάσης μπορεί να συσχετιστεί n-διαστασιακός χώρος φάσης.)

Τώρα ας αρχίσουμε να επηρεάζουμε τα εκκρεμή μας με ένα εξωτερικό περιοδικό σήμα. Η απόκριση γραμμικών και μη γραμμικών συστημάτων θα είναι διαφορετική. Στην πρώτη περίπτωση, θα δημιουργηθούν σταδιακά κανονικές περιοδικές ταλαντώσεις με την ίδια συχνότητα με τη συχνότητα του σήματος εξαναγκασμού. Στο επίπεδο φάσης, μια τέτοια κίνηση αντιστοιχεί σε μια κλειστή καμπύλη που ονομάζεται ελκυστής(από το αγγλικό ρήμα να προσελκύσει -προσέλκυση), - ένα σύνολο τροχιών που χαρακτηρίζουν μια διαδικασία σταθερής κατάστασης. Στην περίπτωση ενός μη γραμμικού εκκρεμούς, σύνθετες, μη περιοδικές ταλαντώσεις μπορεί να συμβούν όταν η τροχιά στο επίπεδο φάσης δεν κλείνει για αυθαίρετα μεγάλο χρονικό διάστημα. Σε αυτή την περίπτωση, η συμπεριφορά ενός ντετερμινιστικού συστήματος θα μοιάζει εξωτερικά με μια εντελώς τυχαία διαδικασία - αυτό είναι το φαινόμενο δυναμικό ή ντετερμινιστικό χάος. Η εικόνα του χάους στο χώρο φάσης - χαοτικός ελκυστήρας- έχει πολύ περίπλοκη δομή: είναι φράκταλ. Λόγω των ασυνήθιστων ιδιοτήτων του ονομάζεται επίσης παράξενος ελκυστήρας .

Γιατί ένα σύστημα που αναπτύσσεται σύμφωνα με καλά καθορισμένους νόμους συμπεριφέρεται χαοτικά; Η επιρροή των εξωτερικών πηγών θορύβου, καθώς και η κβαντική πιθανότητα, δεν έχουν καμία σχέση με αυτήν στην περίπτωση. Το χάος δημιουργείται από τη δική του δυναμική ενός μη γραμμικού συστήματος - την ικανότητά του να διαχωρίζει εκθετικά γρήγορα αυθαίρετα στενές τροχιές. Ως αποτέλεσμα, το σχήμα των τροχιών εξαρτάται πολύ από τις αρχικές συνθήκες. Ας εξηγήσουμε τι σημαίνει αυτό χρησιμοποιώντας το παράδειγμα ενός μη γραμμικού ταλαντωτικού κυκλώματος υπό την επίδραση ενός εξωτερικού περιοδικού σήματος. Ας εισάγουμε μια μικρή διαταραχή στο σύστημά μας - αλλάξτε ελαφρώς την αρχική φόρτιση του πυκνωτή. Τότε οι ταλαντώσεις στα διαταραγμένα και μη διαταραγμένα κυκλώματα, αρχικά πρακτικά σύγχρονες, πολύ σύντομα θα γίνουν εντελώς διαφορετικές. Δεδομένου ότι σε ένα πραγματικό φυσικό πείραμα είναι δυνατό να τεθούν οι αρχικές συνθήκες μόνο με πεπερασμένη ακρίβεια, είναι αδύνατο να προβλεφθεί η συμπεριφορά των χαοτικών συστημάτων για μεγάλο χρονικό διάστημα.

Πρόβλεψη του μέλλοντος

- Εξαιτίας ενός τόσο μικρού πράγματος! Λόγω πεταλούδας! - φώναξε ο Έκελς.
Έπεσε στο πάτωμα - ένα χαριτωμένο πλασματάκι ικανό να σπάσει την ισορροπία, έπεσαν μικρά ντόμινο... μεγάλα ντόμινο... τεράστια ντόμινο, που συνδέονται με μια αλυσίδα αμέτρητων ετών που συνθέτουν τον Χρόνο.
R. Bradbury. A Sound of Thunder

Πόσο οργανωμένη είναι η ζωή μας; Είναι προκαθορισμένα σε αυτό ορισμένα γεγονότα; Τι είναι προβλέψιμο για πολλά χρόνια εκ των προτέρων και τι δεν υπόκειται σε καμία αξιόπιστη πρόβλεψη ακόμη και για μικρά χρονικά διαστήματα;

Ένα άτομο πρέπει συνεχώς να αντιμετωπίζει τόσο τακτοποιημένες όσο και άτακτες διαδικασίες που δημιουργούνται από διάφορα δυναμικά συστήματα. Γνωρίζουμε ότι ο Ήλιος ανατέλλει και δύει κάθε 24 ώρες, και αυτό θα συνεχιστεί σε όλη μας τη ζωή. Μετά τον χειμώνα, έρχεται πάντα η άνοιξη και είναι απίθανο να γίνει ποτέ το αντίστροφο. Οι επιχειρήσεις κοινής ωφέλειας που μας παρέχουν φως και θερμότητα, ιδρύματα και καταστήματα, καθώς και συστήματα μεταφορών (λεωφορεία, τρόλεϊ, μετρό, αεροπλάνα, τρένα) λειτουργούν λίγο πολύ τακτικά. Οι διαταραχές στη ρυθμική λειτουργία αυτών των συστημάτων προκαλούν θεμιτή αγανάκτηση και αγανάκτηση στους πολίτες. Εάν οι αποτυχίες συμβαίνουν επανειλημμένα, μιλούν για χάος, εκφράζοντας αρνητική στάση απέναντι σε τέτοια φαινόμενα.

Αλλά ταυτόχρονα, υπάρχουν διαδικασίες που είναι γνωστές για την απρόβλεπτη τους ικανότητα. Για παράδειγμα, όταν πετάμε ένα νόμισμα, ποτέ δεν ξέρουμε ακριβώς τι θα προκύψει - κεφάλια ή ουρές. Τέτοια απρόβλεπτα δεν προκαλεί συναγερμό. Μπορεί να οδηγήσει σε πολύ πιο δραματικές συνέπειες όταν παίζετε ρουλέτα, αλλά όσοι τους αρέσει να δελεάζουν τη μοίρα παίρνουν συνειδητά αυτό το ρίσκο.

Γιατί ορισμένες διαδικασίες είναι προβλέψιμες στα αποτελέσματά τους, ενώ άλλες όχι; Ίσως απλά δεν έχουμε αρκετά αρχικά δεδομένα για μια καλή πρόβλεψη; Πρέπει να βελτιώσετε τις γνώσεις σας για τις αρχικές συνθήκες - και όλα θα πάνε καλά, τόσο με το νόμισμα όσο και με την πρόβλεψη καιρού. Ο Laplace είπε: δώστε μου τις αρχικές συνθήκες για ολόκληρο το Σύμπαν και θα υπολογίσω το μέλλον του. Ο Laplace έκανε λάθος: αυτός και οι σύγχρονοί του δεν γνώριζαν παραδείγματα ντετερμινιστικών δυναμικών συστημάτων, η συμπεριφορά των οποίων δεν μπορεί να προβλεφθεί για μεγάλο χρονικό διάστημα. Μόλις στα τέλη του 19ου αιώνα ο Γάλλος μαθηματικός Henri Poincaré ένιωσε για πρώτη φορά ότι αυτό ήταν δυνατό. Ωστόσο, πέρασαν άλλα τρία τέταρτα του αιώνα πριν ξεκινήσει η εποχή της έντονης μελέτης του ντετερμινιστικού χάους.

Τα δυναμικά συστήματα μπορούν να χωριστούν σε δύο τύπους. Για τους πρώτους, οι τροχιές κίνησης είναι σταθερές και δεν μπορούν να αλλάξουν σημαντικά από μικρές διαταραχές. Τέτοια συστήματα είναι προβλέψιμα - γι' αυτό ξέρουμε ότι ο Ήλιος θα ανατείλει αύριο, σε ένα χρόνο και σε εκατό χρόνια. Για να προσδιορίσουμε το μέλλον σε αυτή την περίπτωση, αρκεί να γνωρίζουμε τις εξισώσεις κίνησης και να ορίσουμε τις αρχικές συνθήκες. Μικρές αλλαγές στις τιμές των τελευταίων θα οδηγήσουν μόνο σε ένα ασήμαντο σφάλμα στην πρόβλεψη.

Ένας άλλος τύπος περιλαμβάνει δυναμικά συστήματα των οποίων η συμπεριφορά είναι ασταθής, έτσι ώστε τυχόν διαταραχές, όσο μικρές, γρήγορα (σε χρονική κλίμακα χαρακτηριστική αυτού του συστήματος) οδηγούν σε ριζική αλλαγή στην τροχιά. Όπως σημείωσε ο Πουανκαρέ στο έργο του «Science and Method» (1908), στα ασταθή συστήματα «μια εντελώς ασήμαντη αιτία, που μας διαφεύγει λόγω της μικρότητάς της, προκαλεί ένα σημαντικό αποτέλεσμα που δεν μπορούμε να προβλέψουμε. (...) Η πρόβλεψη γίνεται αδύνατη. έχουμε μπροστά μας ένα τυχαίο φαινόμενο». Έτσι, η πρόβλεψη για μεγάλες χρονικές περιόδους χάνει κάθε νόημα.

Το παράδειγμα μη γραμμικού ταλαντωτικού κυκλώματος που συζητήθηκε παραπάνω δείχνει ότι χαοτική συμπεριφορά με απρόβλεπτο μέλλον μπορεί να συμβεί ακόμη και σε πολύ απλά συστήματα.

Ανασυγκρότηση του παρελθόντος

Επομένως, η πρόβλεψη του μέλλοντος δεν είναι πάντα δυνατή. Τι γίνεται με το παρελθόν; Είναι πάντα δυνατό να ανασυνθέσουμε ("προβλέψουμε", ερμηνεύσουμε ξεκάθαρα) το παρελθόν; Φαίνεται ότι δεν πρέπει να υπάρχουν προβλήματα εδώ. Εφόσον οι τροχιές απομακρύνονται η μία από την άλλη όταν κινούνται προς τα εμπρός, πρέπει να πλησιάζουν η μία την άλλη όταν κινούνται προς τα πίσω. Ετσι οπως ειναι. Ωστόσο, δεν υπάρχει μία, αλλά πολλές κατευθύνσεις κατά τις οποίες μπορεί να συμβεί σύγκλιση ή απόκλιση τροχιών στο χώρο φάσης. Όταν κινείστε προς τα εμπρός και προς τα πίσω, οι τροχιές μπορεί να συγκλίνουν κατά μήκος του ενός τμήματος των κατευθύνσεων, αλλά να αποκλίνουν κατά μήκος του άλλου.

Είναι το παρελθόν «απρόβλεπτο»; Ανοησίες! Άλλωστε κάτι έχει ήδη συμβεί. Όλα είναι γνωστά... Ας σκεφτούμε όμως. Αν όλα ήταν τόσο απλά με την ανοικοδόμηση του παρελθόντος, πώς θα μπορούσε για κάποιους ο Νικόλαος Β' να είναι ακόμα ματωμένος, αλλά για άλλους να είναι άγιος; Και ποιος είναι ο Στάλιν: ιδιοφυΐα ή κακοποιός; Ας αγνοήσουμε προς το παρόν το πρόβλημα του πόσο ελεύθεροι ήταν να λάβουν ορισμένες αποφάσεις, σε ποιο βαθμό αυτές οι αποφάσεις ήταν προκαθορισμένες από τις περιστάσεις και ποιες θα μπορούσαν να είναι οι συνέπειες των εναλλακτικών αποφάσεων. Ας θεωρήσουμε την ιστορική διαδικασία ως τη δυναμική κάποιου υποθετικού χαοτικού συστήματος. Στη συνέχεια, όταν προσπαθούμε να ανασυνθέσουμε το παρελθόν, θα βρεθούμε αντιμέτωποι με έναν ραγδαία αυξανόμενο αριθμό επιλογών (τροχιών) που αντιστοιχούν στην τρέχουσα κατάσταση του συστήματος. Μόνο ένα από αυτά αντιστοιχεί στην πραγματική εξέλιξη των γεγονότων. Αν επιλέξετε όχι αυτόν, αλλά κάποιον άλλο, θα έχετε μια παραμορφωμένη «έκδοση» της ιστορίας. Με ποια βάση επιλέγεται η σωστή τροχιά («έκδοση»); Οι πληροφορίες στις οποίες μπορούμε να βασιστούμε είναι το σύνολο των διαθέσιμων συγκεκριμένων γεγονότων. Οι τροχιές που δεν είναι συμβατές με αυτές απορρίπτονται. Ως αποτέλεσμα, δεδομένων αρκετά αξιόπιστων γεγονότων, θα υπάρξει μια τροχιά που θα ορίζει μια ενιαία εκδοχή της ιστορίας. Ωστόσο, ακόμη και για το πρόσφατο παρελθόν μπορεί να υπάρχουν πολύ περισσότερες τροχιές από αξιόπιστες πληροφορίες - τότε δεν μπορεί πλέον να γίνει μια σαφής ερμηνεία της ιστορικής διαδικασίας. Και όλα αυτά με μια ευσυνείδητη και σεβαστή στάση απέναντι στην ιστορία και τα γεγονότα. Τώρα προσθέστε εδώ τις προκαταλήψεις των πρωτογενών πηγών, την απώλεια ορισμένων πληροφοριών με την πάροδο του χρόνου, τη χειραγώγηση των γεγονότων στο στάδιο της ερμηνείας (φίμωση ορισμένων, προεξέχοντα άλλα, παραποίηση κ.λπ.) - και η αντικατάσταση του μαύρου με το λευκό δεν θα είναι τόσο δύσκολη υπόθεση . Και το πιο ενδιαφέρον είναι ότι, αν χρειαστεί, οι ίδιοι διερμηνείς μετά από κάποιο χρονικό διάστημα μπορούν εύκολα να ισχυριστούν το αντίθετο. Είναι γνωστή αυτή η εικόνα;

Έτσι, η δυναμική φύση του «απρόβλεπτου» του παρελθόντος είναι παρόμοια με τη φύση του απρόβλεπτου του μέλλοντος: αστάθεια των τροχιών ενός δυναμικού συστήματος και ταχεία αύξηση του αριθμού των πιθανών επιλογών καθώς απομακρύνεται κανείς από την αρχή. σημείο. Για την ανασύσταση του παρελθόντος, εκτός από το ίδιο το δυναμικό σύστημα, χρειάζονται πληροφορίες από αυτό το παρελθόν, επαρκείς σε ποσότητα και αξιόπιστες σε ποιότητα. Πρέπει να σημειωθεί ότι σε διαφορετικά σημεία της ιστορικής διαδικασίας ο βαθμός του χάους της είναι διαφορετικός και μπορεί ακόμη και να πέσει στο μηδέν (μια κατάσταση όπου όλα τα ουσιαστικά είναι προκαθορισμένα). Φυσικά, όσο λιγότερο χαοτικό είναι το σύστημα, τόσο πιο εύκολο είναι να ανακατασκευαστεί το παρελθόν του.

Μπορούμε να ελέγξουμε το χάος;

Το χάος συχνά γεννά ζωή.
G. Adams

Με την πρώτη ματιά, η φύση του χάους αποκλείει τη δυνατότητα να το ελέγξουμε. Στην πραγματικότητα, ισχύει το αντίθετο: η αστάθεια των τροχιών των χαοτικών συστημάτων τα καθιστά εξαιρετικά ευαίσθητα στον έλεγχο.

Έστω, για παράδειγμα, απαιτείται η μεταφορά ενός συστήματος από μια κατάσταση σε άλλη (για να μετακινηθεί μια τροχιά από ένα σημείο του χώρου φάσης σε ένα άλλο). Το απαιτούμενο αποτέλεσμα μπορεί να επιτευχθεί μέσα σε ένα δεδομένο χρονικό διάστημα από μία ή μια σειρά από λεπτές, ασήμαντες διαταραχές των παραμέτρων του συστήματος. Καθένα από αυτά θα αλλάξει ελαφρώς μόνο την τροχιά, αλλά μετά από κάποιο χρονικό διάστημα η συσσώρευση και η εκθετική ενίσχυση μικρών διαταραχών θα οδηγήσει σε σημαντική διόρθωση της κίνησης. Σε αυτή την περίπτωση, η τροχιά θα παραμείνει στον ίδιο χαοτικό ελκυστήρα. Έτσι, τα συστήματα με χάος επιδεικνύουν τόσο καλή δυνατότητα ελέγχου όσο και εκπληκτική πλαστικότητα: αντιδρώντας με ευαισθησία σε εξωτερικές επιρροές, διατηρούν τον τύπο κίνησης.

Σύμφωνα με πολλούς ερευνητές, είναι ο συνδυασμός αυτών των δύο ιδιοτήτων που προκαλεί χαοτική δυναμική για να χαρακτηρίσει τη συμπεριφορά πολλών συστημάτων ζωντανών οργανισμών. Για παράδειγμα, η χαοτική φύση του καρδιακού ρυθμού του επιτρέπει να ανταποκρίνεται με ευελιξία στις αλλαγές του σωματικού και συναισθηματικού στρες, προσαρμοζόμενος σε αυτές. Είναι γνωστό ότι η ρύθμιση του καρδιακού ρυθμού οδηγεί σε θάνατο μετά από κάποιο χρονικό διάστημα. Ένας λόγος είναι ότι η καρδιά μπορεί να μην έχει αρκετή «μηχανική δύναμη» για να αντισταθμίσει τις εξωτερικές διαταραχές. Στην πραγματικότητα, η κατάσταση είναι πιο σύνθετη. Η τάξη του έργου της καρδιάς χρησιμεύει ως δείκτης μείωσης του χάους σε άλλα συστήματα που σχετίζονται με αυτό. Η κανονικότητα υποδηλώνει μείωση της αντίστασης του σώματος σε τυχαίες επιρροές του εξωτερικού περιβάλλοντος, όταν δεν είναι πλέον σε θέση να παρακολουθεί επαρκώς τις αλλαγές και να ανταποκρίνεται με ευελιξία σε αυτές.

Είναι προφανές ότι κάθε πολύπλοκο σύστημα που λειτουργεί σε ένα μεταβαλλόμενο περιβάλλον θα πρέπει να έχει τέτοια πλαστικότητα και δυνατότητα ελέγχου. Αυτό είναι το κλειδί για τη διατήρησή τους και την επιτυχή εξέλιξή τους.

Από το χάος στην τάξη

Πώς διασφαλίζεται η ακεραιότητα και η σταθερότητα των ζωντανών οργανισμών και άλλων πολύπλοκων συστημάτων εάν τα επιμέρους μέρη τους συμπεριφέρονται χαοτικά;

Αποδεικνύεται ότι εκτός από το χάος σε πολύπλοκα μη γραμμικά συστήματα, είναι επίσης πιθανό το αντίθετο φαινόμενο, το οποίο θα μπορούσε να ονομαστεί αντι-χάος. Εάν συνδεθούν χαοτικά υποσυστήματα μεταξύ τους, μπορεί να προκύψει αυθόρμητη τακτοποίησή τους («κρυστάλλωση») με αποτέλεσμα να αποκτήσουν τα χαρακτηριστικά ενός ενιαίου συνόλου. Η απλούστερη έκδοση αυτής της παραγγελίας είναι χαοτικός συγχρονισμός, όταν όλα τα υποσυστήματα που συνδέονται μεταξύ τους κινούνται, αν και χαοτικά, αλλά εξίσου, συγχρονισμένα. Διαδικασίες χαοτικός συγχρονισμόςμπορεί να εμφανιστεί όχι μόνο στο σώμα των ζώων και των ανθρώπων, αλλά και σε μεγαλύτερες δομές - βιοκαινώσεις, δημόσιους οργανισμούς, πολιτείες, συστήματα μεταφορών κ.λπ.

Τι καθορίζει τη δυνατότητα συγχρονισμού; Πρώτον, η συμπεριφορά κάθε επιμέρους υποσυστήματος: όσο πιο χαοτικό και «ανεξάρτητο» είναι, τόσο πιο δύσκολο είναι να το αναγκάσεις να «λογαριάσει» με άλλα στοιχεία του συνόλου. Δεύτερον, η συνολική ισχύς της σύνδεσης μεταξύ των υποσυστημάτων: η αύξησή της καταστέλλει την τάση προς την «ανεξαρτησία» και μπορεί, καταρχήν, να οδηγήσει σε παραγγελία. Ταυτόχρονα, είναι σημαντικό να υπάρχουν συνδέσεις παγκόσμια, δηλαδή δεν υπήρχαν μόνο μεταξύ γειτονικών, αλλά και μεταξύ στοιχείων που απείχαν πολύ μεταξύ τους.

Σε πραγματικά συστήματα, συμπεριλαμβανομένου ενός μεγάλου αριθμού υποσυστημάτων, η επικοινωνία πραγματοποιείται μέσω ροών υλικού ή πληροφοριών. Όσο πιο έντονες είναι, τόσο μεγαλύτερη είναι η πιθανότητα τα στοιχεία να συμπεριφέρονται με συνέπεια, και το αντίστροφο. Για παράδειγμα, σε ένα κράτος, ο ρόλος της σύνδεσης των ροών διαδραματίζεται από τις μεταφορές, το ταχυδρομείο, τις τηλεφωνικές επικοινωνίες κ.λπ. Επομένως, η αύξηση των τιμολογίων για αυτές τις υπηρεσίες, στην περίπτωση που οδηγεί σε μείωση των αντίστοιχων ροών, αποδυναμώνει την ακεραιότητα του κράτους και συμβάλλει στην καταστροφή του.

Από τη θεωρία του χαοτικού συγχρονισμού προκύπτει ότι η συντονισμένη λειτουργία μεμονωμένων μερών ενός σύνθετου συστήματος μπορεί να εξασφαλιστεί από ένα από τα στοιχεία του, που ονομάζεται ρούμι βηματοδότη, ή «βηματοδότης». Όντας μονόδρομα συνδεδεμένος με όλα τα στοιχεία του συστήματος, «καθοδηγεί» την κίνησή τους, επιβάλλοντας τον δικό του ρυθμό. Αν το κάνουμε έτσι ώστε τα επιμέρους υποσυστήματα να μην συνδέονται μεταξύ τους, αλλά μόνο με τον βηματοδότη, έχουμε την περίπτωση ενός εξαιρετικά συγκεντρωτικού συστήματος. Σε ένα κράτος, για παράδειγμα, τον ρόλο του «βηματοδότη» επιτελεί η κεντρική κυβέρνηση και... τα ΜΜΕ που λειτουργούν σε ολόκληρη ή σημαντικό τμήμα της επικράτειας της χώρας. Σήμερα αυτό ισχύει ιδιαίτερα για τα ηλεκτρονικά μέσα, καθώς υπερέχουν σημαντικά από άλλα όσον αφορά την κινητικότητα και τη γενική ροή πληροφοριών. Κατανοώντας αυτό διαισθητικά, η κεντρική κυβέρνηση προσπαθεί να κρατήσει τα μέσα ενημέρωσης υπό έλεγχο και επίσης περιορίζει την επιρροή καθενός από αυτά ξεχωριστά. Διαφορετικά, δεν θα κυβερνά πλέον το κράτος.

Εδώ θίξαμε ένα πολύ σημαντικό θέμα. Δεδομένου ότι η μέση ισχύς των συνδέσεων είναι μια συνοπτική παράμετρος, η οποία περιλαμβάνει τόσο υλικές όσο και πληροφοριακές συνδέσεις, αυτό σημαίνει ότι η αποδυνάμωση ορισμένων από αυτές μπορεί να αντισταθμιστεί με την ενίσχυση άλλων. Το πιο απλό παράδειγμα είναι η αντικατάσταση πραγματικών αγαθών με χαρτί ή ακόμα και ηλεκτρονικό χρήμα. Σε αυτήν την περίπτωση, ο προμηθευτής, στην πραγματικότητα, αντί για ένα υλικό προϊόν, λαμβάνει πληροφορίες σχετικά με μια αλλαγή στον λογαριασμό του - και είναι πολύ ευχαριστημένος με μια τέτοια ανταλλαγή. Με τον ίδιο τρόπο κερδίζονται ή χάνονται καθημερινά τεράστια χρηματικά ποσά μέσω χρηματιστηριακών συναλλαγών, τα οποία, τελικά, κάποιος πρέπει να αντισταθμίσει σε πραγματικά προϊόντα ή υπηρεσίες.

Πώς μπορεί να καταστραφεί μια συγχρονισμένη κατάσταση;

Έχουμε ήδη αναφέρει μια πιθανότητα. Αυτό είναι μια αποδυνάμωση των δεσμών. Ένας άλλος λόγος είναι η ανεπαρκής επιρροή του «βηματοδότη» στο σύνολο. Πράγματι, εάν ο «ρυθμός» που υπαγορεύει ο βηματοδότης είναι πολύ αντίθετος με τη φυσική συμπεριφορά των στοιχείων του συστήματος, τότε ακόμη και με επαρκή ισχύ σύνδεσης δεν θα μπορεί να επιβάλει τη γραμμή συμπεριφοράς του στο σύνολο. Ωστόσο, η προηγούμενη συμπεριφορά δεν θα παραμείνει ίδια. Ως αποτέλεσμα, ο συγχρονισμός θα καταστραφεί.

Fractality και σταθερότητα

Έχουμε ήδη δει ότι η θεωρία του δυναμικού χάους μπορεί να εφαρμοστεί σε πολλά συστήματα, συμπεριλαμβανομένου του κράτους και της κοινωνίας στο σύνολό της. Τι ρόλο παίζει η δομή φράκταλ του χάους σε αυτό; Άλλωστε, η εικόνα του χάους στο χώρο φάσης - ένας παράξενος ελκυστής - είναι γεωμετρικά ένα φράκταλ. Παρά το γεγονός ότι κάθε μεμονωμένη χαοτική τροχιά είναι εξαιρετικά ευαίσθητη στις παραμικρές διαταραχές, ένας παράξενος ελκυστής (το σύνολο όλων των πιθανών τροχιών) είναι μια πολύ σταθερή δομή. Έτσι, το δυναμικό χάος μοιάζει με έναν διπρόσωπο Ιανό: από τη μια, εκδηλώνεται ως πρότυπο αταξίας και από την άλλη, ως σταθερότητα και τάξη σε διαφορετικές κλίμακες.

Αν το σκεφτείς, είναι εύκολο να δεις ότι στην κοινωνία, όπως και στη φύση, πολλά συστήματα είναι χτισμένα με βάση την αρχή των φράκταλ: ορισμένα συμπλέγματα σχηματίζονται από μικρά στοιχεία, αυτά με τη σειρά τους χρησιμεύουν ως στοιχεία για μεγαλύτερα συμπλέγματα κ.λπ. για παράδειγμα, είναι οργανωμένες βιώσιμες οικονομικές και παραγωγικές δομές; Δύο ακραίες θέσεις: μεγάλες διεθνικές εταιρείες και «μικρές επιχειρήσεις». Κάθε ένα από αυτά χωριστά είναι μη βιώσιμο. Οι μεγάλες εταιρείες, με τεράστια οικονομική ισχύ, είναι ανενεργές και δεν μπορούν να ανταποκριθούν γρήγορα στις αλλαγές στο περιβάλλον οικονομικό περιβάλλον. Η «μικρή επιχείρηση» δεν είναι ικανή να λύσει μεγάλα προβλήματα ή να εξασφαλίσει ανάπτυξη υποδομών. Πού είναι η χρυσή τομή; Σε μεσαίες επιχειρήσεις; Καθόλου. Μια βιώσιμη οικονομική υποδομή παρέχεται (με την απαραίτητη άντληση των απαραίτητων πόρων) από ένα σύνολο οικονομικών αντικειμένων διαφορετικής κλίμακας (εδώ είναι ένα φράκταλ!) που σχηματίζουν μια πυραμίδα. Στη βάση υπάρχουν πολλές μικρές εταιρείες και επιχειρήσεις, ψηλότερα στην πυραμίδα το μέγεθος των επιχειρήσεων αυξάνεται σταδιακά, και ο αριθμός τους, κατά συνέπεια, μειώνεται και, τέλος, στην κορυφή υπάρχουν οι μεγαλύτερες εταιρείες. Αυτή η δομή είναι χαρακτηριστική, για παράδειγμα, της οικονομίας των ΗΠΑ. Ταυτόχρονα, οι μικρές επιχειρήσεις είναι οι πιο κινητές: συχνά γεννιούνται και πεθαίνουν, αποτελώντας τους κύριους προμηθευτές νέων ιδεών και τεχνολογιών. Οι καινοτομίες που έχουν αναπτυχθεί επαρκώς επιτρέπουν σε ορισμένες επιχειρήσεις να αναπτυχθούν στο επόμενο επίπεδο ή να μεταφέρουν (πουλήσουν) συσσωρευμένες καινοτομίες σε μεγαλύτερες εταιρείες. Εάν το περιβάλλον είναι επαρκώς δεκτικό, ένας τέτοιος μηχανισμός μπορεί να δημιουργήσει νέες βιομηχανίες και οικονομίες σε λίγα χρόνια. Δεν είναι χωρίς λόγο ότι στη λεγόμενη «νέα οικονομία» ο κύριος όγκος ακόμη και μεγάλων επιχειρήσεων είναι εταιρείες που πριν από 15-20 χρόνια είτε δεν υπήρχαν καθόλου είτε ταξινομούνταν ως μικρές.

Ενα άλλο παράδειγμα. Κατά τη διάρκεια της περεστρόικα, πολλά γράφτηκαν και ειπώθηκαν για τη «λάθος» δομή της ΕΣΣΔ, στην οποία το κράτος είχε μια περίπλοκη ιεραρχική δομή, οργανωμένη σύμφωνα με την αρχή της matryoshka. Τι προσφέρθηκε ως αντάλλαγμα; Κάθε έθνος έχει τον δικό του μητρικό στρατό, τη δική του γλώσσα, τη δική του «ελίτ», τους δικούς του ηγέτες των φυλών. Ακούγεται καλό. Τώρα κοιτάξτε πώς εξελίχθηκε αυτή η ιδέα για πολλούς λαούς της πρώην ΕΣΣΔ και της Γιουγκοσλαβίας... Από τη σκοπιά της θεωρίας της σταθερότητας, η ιδέα μιας ομοιογενούς δομής του ρωσικού κράτους είναι ιδέα ενός ηττημένου. Γιατί; Η αρχή matryoshka είναι, στην πραγματικότητα, μια αρχή φράκταλ, χάρη στην οποία ένα χαοτικό σύστημα αποκτά δομή και σταθερότητα. Η ΕΣΣΔ και η Ρωσική Αυτοκρατορία χτίστηκαν στην αρχή των φράκταλ συστημάτων και αυτό εξασφάλιζε τη σταθερότητά τους ως κράτη. Σε διαφορετικά επίπεδα, οι φυσικές πολιτειακές, εθνοτικές, εδαφικές και άλλες οντότητες με εύρυθμους μηχανισμούς εσωτερικής λειτουργίας, με δικά τους δικαιώματα και ευθύνες, διανθίστηκαν στο συνολικό σύστημα.

Το χάος γεννά πληροφορίες

Έχουμε ήδη διαπιστώσει ότι η συμπεριφορά των χαοτικών συστημάτων δεν μπορεί να προβλεφθεί σε μεγάλα χρονικά διαστήματα. Καθώς απομακρύνεστε από τις αρχικές συνθήκες, η θέση της τροχιάς γίνεται όλο και πιο αβέβαιη. Από την άποψη της θεωρίας της πληροφορίας, αυτό σημαίνει ότι το ίδιο το σύστημα παράγει πληροφορίες και η ταχύτητα αυτής της διαδικασίας είναι μεγαλύτερη, τόσο μεγαλύτερος είναι ο βαθμός χάους. Από εδώ, σύμφωνα με τη θεωρία του χαοτικού συγχρονισμού που συζητήθηκε προηγουμένως, ακολουθεί ένα ενδιαφέρον συμπέρασμα: όσο πιο έντονα το σύστημα παράγει πληροφορίες, τόσο πιο δύσκολο είναι να τις συγχρονίσετε, να το αναγκάσετε να συμπεριφέρεται κάπως διαφορετικά.

Αυτός ο κανόνας φαίνεται να ισχύει για οποιοδήποτε σύστημα παραγωγής πληροφοριών. Για παράδειγμα, εάν μια συγκεκριμένη δημιουργική ομάδα δημιουργεί επαρκή αριθμό ιδεών και ΕΝΑδουλεύοντας ενεργά σε τρόπους εφαρμογής τους, είναι πιο δύσκολο γι 'αυτόν να επιβάλει απ' έξω κάποια γραμμή συμπεριφοράς που είναι ανεπαρκής για τις δικές του απόψεις. Και αντίστροφα, εάν, παρουσία των ίδιων υλικών ροών και πόρων, η ομάδα συμπεριφέρεται παθητικά με την έννοια της πληροφορίας, δεν δημιουργεί ιδέες ή δεν τις εφαρμόζει - με άλλα λόγια, ακολουθεί την αρχή «...ζεστό και υγρό ” - τότε είναι πολύ εύκολο να το υποτάξεις .

Χαοτικοί υπολογιστές

Τι μας λείπει στους σύγχρονους υπολογιστές; Εάν ένας ζωντανός οργανισμός, για να υπάρχει σε ένα μεταβαλλόμενο περιβάλλον, πρέπει να έχει στοιχεία χαοτικής συμπεριφοράς, τότε μπορεί να υποτεθεί ότι τα τεχνητά συστήματα ικανά να αλληλεπιδρούν επαρκώς με ένα μεταβαλλόμενο περιβάλλον πρέπει να είναι χαοτικά στον ένα ή τον άλλο βαθμό. Οι σύγχρονοι υπολογιστές δεν είναι έτσι. Είναι κλειστά συστήματα με πολύ μεγάλο αλλά πεπερασμένο αριθμό καταστάσεων. Ίσως στο μέλλον, στη βάση του δυναμικού χάους, να δημιουργηθεί ένας νέος τύπος υπολογιστή - συστήματα ανοιχτά από θερμοδυναμική άποψη, ικανά να προσαρμοστούν στις περιβαλλοντικές συνθήκες.

Ωστόσο, σήμερα χαοτικοί αλγόριθμοι μπορούν να χρησιμοποιηθούν με επιτυχία στις τεχνολογίες υπολογιστών για την αποθήκευση, την αναζήτηση και την προστασία πληροφοριών. Κατά την επίλυση ορισμένων προβλημάτων, αποδεικνύονται πιο αποτελεσματικά από τις παραδοσιακές μεθόδους. Αυτό ισχύει ιδιαίτερα για την εργασία με δεδομένα πολυμέσων. Σε αντίθεση με τα κείμενα και τα προγράμματα, οι πληροφορίες πολυμέσων απαιτούν διαφορετικό τρόπο οργάνωσης της μνήμης. Το απόλυτο όνειρο των χρηστών είναι η δυνατότητα αναζήτησης μιας μελωδίας, βίντεο ή απαραίτητων φωτογραφιών όχι με βάση τα χαρακτηριστικά τους (όνομα καταλόγου και αρχείου, ημερομηνία δημιουργίας κ.λπ.), αλλά με βάση το περιεχόμενο ή τη συσχέτιση, έτσι ώστε, για παράδειγμα, χρησιμοποιώντας ένα κομμάτι μιας μελωδίας μπορεί κανείς να βρει και να παίξει ένα μουσικό έργο. Αποδεικνύεται ότι μια τέτοια συνειρμική αναζήτηση μπορεί να επιτευχθεί χρησιμοποιώντας τεχνολογίες που βασίζονται στο ντετερμινιστικό χάος. Πως?

Έχουμε ήδη συζητήσει τη δημιουργία πληροφοριών από χαοτικά συστήματα. Τώρα ας αναρωτηθούμε: είναι δυνατόν να αντιστοιχίσουμε την τροχιά με συγκεκριμένα δεδομένα γραμμένα με τη μορφή μιας συγκεκριμένης ακολουθίας συμβόλων; Τότε μερικές από τις τροχιές του συστήματος θα ήταν σε αντιστοιχία ένα προς ένα με τις αλληλουχίες πληροφοριών μας. Και δεδομένου ότι κάθε τροχιά είναι μια λύση στις εξισώσεις κίνησης του συστήματος κάτω από ορισμένες αρχικές συνθήκες, τότε οποιαδήποτε ακολουθία συμβόλων θα μπορούσε να αποκατασταθεί λύνοντας αυτές τις εξισώσεις, θέτοντας ένα μικρό κομμάτι της ως αρχικές συνθήκες. Αυτό θα καθιστούσε δυνατή την αναζήτηση πληροφοριών συνειρμικά, δηλαδή αναζήτηση βάσει περιεχομένου.

Μια ομάδα εργαζομένων στο ινστιτούτο μας δημιούργησε μαθηματικά μοντέλα για την καταγραφή, την αποθήκευση και την ανάκτηση πληροφοριών χρησιμοποιώντας τις τροχιές δυναμικών συστημάτων με χάος. Αν και οι αλγόριθμοι φαίνονταν πολύ απλοί, η δυνητική τους χωρητικότητα πληροφοριών ξεπέρασε σημαντικά την ποσότητα όλων των πληροφοριών που ήταν διαθέσιμες στο Διαδίκτυο. Η ανάπτυξη της ιδέας οδήγησε στη δημιουργία μιας τεχνολογίας που επιτρέπει την επεξεργασία κάθε είδους δεδομένων: εικόνων, κειμένου, ψηφιακής μουσικής, ομιλίας, σημάτων κ.λπ. (RF Patent 2050072, US Patent 5774587, Canadian Patent 2164417).

Ένα παράδειγμα χρήσης της τεχνολογίας είναι το πακέτο λογισμικού Forget-Me-Not, σχεδιασμένο για εργασία με αρχεία αδόμητων πληροφοριών τόσο σε προσωπικούς υπολογιστές όσο και σε διακομιστές πληροφοριών. Το Forget-me-no υλοποιείται ως μηχανή αναζήτησης που εκτελείται σε τυπικά προγράμματα περιήγησης στο Διαδίκτυο όπως το Netscape και ο Explorer. Όλες οι πληροφορίες στο αρχείο καταγράφονται και αποθηκεύονται με τη μορφή τροχιών ενός χαοτικού συστήματος. Για να αναζητήσει τα απαραίτητα έγγραφα, ο χρήστης συνθέτει ένα αίτημα πληκτρολογώντας σε ελεύθερη μορφή πολλές γραμμές κειμένου που σχετίζονται με το περιεχόμενο του απαιτούμενου εγγράφου. Σε απάντηση, το σύστημα θα παράσχει το απαιτούμενο έγγραφο εάν οι πληροφορίες εισόδου είναι επαρκείς για τη σαφή αναζήτησή του ή θα προσφέρει ένα σύνολο επιλογών. Εάν είναι απαραίτητο, μπορείτε επίσης να λάβετε ένα αντίγραφο φαξ του εγγράφου που βρέθηκε. Η παρουσία σφαλμάτων στο ερώτημα δεν επηρεάζει σημαντικά την ποιότητα της αναζήτησης.

Πρόσθετες πληροφορίες για το σύμπλεγμα Forget-Me-Not, καθώς και μια δοκιμαστική έκδοση του προγράμματος, μπορείτε να λάβετε στη διεύθυνση http://www.cplire.ru.

Επικοινωνία μέσα από το χάος

Τα περισσότερα σύγχρονα συστήματα επικοινωνίας χρησιμοποιούν αρμονικές ταλαντώσεις ως φορέα πληροφοριών. Το σήμα πληροφοριών στον πομπό διαμορφώνει αυτές τις ταλαντώσεις σε πλάτος, συχνότητα ή φάση και στον δέκτη οι πληροφορίες διαχωρίζονται χρησιμοποιώντας την αντίστροφη λειτουργία - αποδιαμόρφωση. Η επιβολή πληροφοριών στο μέσο πραγματοποιείται είτε διαμορφώνοντας ήδη σχηματισμένες αρμονικές ταλαντώσεις, είτε ελέγχοντας τις παραμέτρους της γεννήτριας κατά τη λειτουργία της.

Με παρόμοιο τρόπο, μπορείτε να διαμορφώσετε ένα χαοτικό σήμα. Ωστόσο, οι δυνατότητες εδώ είναι πολύ ευρύτερες. Τα αρμονικά σήματα έχουν μόνο τρία ελεγχόμενα χαρακτηριστικά (πλάτος, φάση και συχνότητα). Στην περίπτωση των χαοτικών ταλαντώσεων, ακόμη και μικρές διακυμάνσεις στην τιμή της παραμέτρου ενός από τα στοιχεία της πηγής χάους οδηγούν σε αλλαγές στη φύση των ταλαντώσεων, οι οποίες μπορούν να καταγραφούν αξιόπιστα από τα όργανα. Αυτό σημαίνει ότι οι πηγές χάους με παραμέτρους μεταβλητών στοιχείων έχουν δυνητικά ένα μεγάλο σύνολο σχημάτων για την εισαγωγή ενός σήματος πληροφοριών σε ένα χαοτικό μέσο (σχήματα διαμόρφωσης). Επιπλέον, το χάος έχει θεμελιωδώς ένα ευρύ φάσμα συχνοτήτων, δηλαδή αναφέρεται σε ευρυζωνικά σήματα, το ενδιαφέρον για το οποίο η ραδιομηχανική συνδέεται παραδοσιακά με τη μεγαλύτερη χωρητικότητα πληροφοριών σε σύγκριση με τις ταλαντώσεις στενής ζώνης. Μια ευρεία ζώνη συχνοτήτων φορέα σάς επιτρέπει να αυξήσετε την ταχύτητα μετάδοσης πληροφοριών, καθώς και να αυξήσετε την αντίσταση του συστήματος σε ενοχλητικούς παράγοντες. Τα συστήματα επικοινωνίας ευρείας ζώνης και υπερευρείας ζώνης που βασίζονται στο χάος έχουν πιθανά πλεονεκτήματα έναντι των παραδοσιακών συστημάτων ευρέος φάσματος όσον αφορά τον καθορισμό παραμέτρων όπως η απλότητα της εφαρμογής υλικού, η ενεργειακή απόδοση και η ταχύτητα μεταφοράς πληροφοριών. Τα χαοτικά σήματα μπορούν επίσης να χρησιμεύσουν για την απόκρυψη πληροφοριών που μεταδίδονται μέσω ενός συστήματος επικοινωνίας χωρίς τη χρήση επέκτασης φάσματος, δηλαδή όταν η ζώνη συχνοτήτων των πληροφοριών και των μεταδιδόμενων σημάτων συμπίπτει.

Ο συνδυασμός αυτών των παραγόντων τόνωσε την ενεργό έρευνα σε χαοτικά συστήματα επικοινωνίας. Επί του παρόντος, έχουν ήδη προταθεί αρκετές προσεγγίσεις για την επέκταση του εύρους των σημάτων πληροφοριών και για την κατασκευή πομπών και δεκτών που είναι απλοί στην αρχιτεκτονική.

Μία από τις τελευταίες ιδέες προς αυτή την κατεύθυνση είναι τα λεγόμενα άμεσα χαοτικά σχήματα επικοινωνίας. Σε ένα σχήμα άμεσης χαοτικής επικοινωνίας, οι πληροφορίες εισάγονται σε ένα χαοτικό σήμα που παράγεται απευθείας στην περιοχή μήκους κύματος ραδιοκυμάτων ή μικροκυμάτων. Η πληροφορία εισάγεται είτε διαμορφώνοντας τις παραμέτρους του πομπού, είτε τοποθετώντας την σε ένα χαοτικό μέσο αφού έχει δημιουργηθεί. Αντίστοιχα, η εξαγωγή ενός σήματος πληροφοριών από ένα χαοτικό πραγματοποιείται επίσης στην περιοχή υψηλών ή υπερυψηλών συχνοτήτων. Οι εκτιμήσεις δείχνουν ότι τα ευρυζωνικά και τα εξαιρετικά ευρυζωνικά συστήματα άμεσης χαοτικής επικοινωνίας είναι ικανά να παρέχουν ταχύτητες μεταφοράς πληροφοριών από δεκάδες megabit ανά δευτερόλεπτο έως αρκετά gigabits ανά δευτερόλεπτο. Το Ινστιτούτο Ραδιομηχανικής και Ηλεκτρονικής της Ρωσικής Ακαδημίας Επιστημών έχει ήδη πραγματοποιήσει πειράματα για την άμεση χαοτική μετάδοση πληροφοριών σε ταχύτητες έως και 70 Mbit/sec.

Χάος και δίκτυα υπολογιστών

Στα σχήματα επικοινωνίας, το χάος μπορεί να χρησιμοποιηθεί ως φορέας πληροφοριών, ως δυναμική διαδικασία που εξασφαλίζει τη μετατροπή της πληροφορίας σε νέα μορφή και, τέλος, ως συνδυασμός και των δύο. Μια συσκευή που μετατρέπει ένα σήμα σε έναν πομπό από έναν τύπο σε άλλο χρησιμοποιώντας χάος ονομάζεται χαοτικός κωδικοποιητής. Με τη βοήθειά του, μπορείτε να αλλάξετε τις πληροφορίες με τέτοιο τρόπο ώστε να είναι απρόσιτες σε έναν εξωτερικό παρατηρητή, αλλά ταυτόχρονα θα επιστρέφονται εύκολα στην αρχική τους μορφή από ένα ειδικό δυναμικό σύστημα - χαοτικός αποκωδικοποιητής, που βρίσκεται στην πλευρά λήψης του συστήματος επικοινωνίας.

Σε ποιες διαδικασίες μπορεί να χρησιμοποιηθεί η χαοτική κωδικοποίηση;

Πρώτον, με τη βοήθειά του είναι δυνατή η οργάνωση του κοινού χώρου πληροφοριών με έναν ριζικά νέο τρόπο, δημιουργώντας μεγάλες ανοιχτές ομάδες χρηστών σε αυτόν - υποχώρους. Μέσα σε κάθε ομάδα, εισάγεται η δική της «γλώσσα» επικοινωνίας - κανόνες, πρωτόκολλα και άλλα χαρακτηριστικά αυτής της «υποκουλτούρας πληροφοριών» που είναι κοινά σε όλους τους συμμετέχοντες. Για όσους επιθυμούν να κατακτήσουν αυτή τη «γλώσσα» και να γίνουν μέλη της κοινότητας, υπάρχουν σχετικά απλά μέσα πρόσβασης. Ταυτόχρονα, θα είναι δύσκολο για εξωτερικούς παρατηρητές να συμμετάσχουν σε μια τέτοια ανταλλαγή. Έτσι, η χαοτική κωδικοποίηση μπορεί να χρησιμεύσει ως μέσο δόμησης του «πληθυσμού» του κοινού χώρου πληροφοριών.

Δεύτερον, η πρόσβαση πολλών χρηστών σε πληροφορίες μπορεί να οργανωθεί με παρόμοιο τρόπο. Η παρουσία του παγκόσμιου δικτύου Διαδικτύου και των κύριων ροών πληροφοριών (Highways) προϋποθέτει την ύπαρξη κοινών πρωτοκόλλων που διασφαλίζουν τη διέλευση των πληροφοριών μέσω κοινών καναλιών. Ωστόσο, σε ορισμένες ομάδες συμμετεχόντων (για παράδειγμα, εντός εταιρικών δικτύων) υπάρχει επείγουσα ανάγκη παροχής πληροφοριών σε συγκεκριμένους καταναλωτές, χωρίς να επιτρέπεται η πρόσβαση σε «ξένους» συμμετέχοντες. Οι χαοτικές μέθοδοι κωδικοποίησης είναι ένα βολικό μέσο οργάνωσης τέτοιων εικονικών εταιρικών δικτύων. Επιπλέον, μπορούν να χρησιμοποιηθούν απευθείας για τη διασφάλιση ενός συγκεκριμένου επιπέδου εμπιστευτικότητας των πληροφοριών, προχωρώντας στον τομέα της παραδοσιακής κρυπτογραφίας.

Τέλος, μια άλλη λειτουργία της χαοτικής κωδικοποίησης είναι πολύ σημαντική σε σχέση με την ανάπτυξη του ηλεκτρονικού εμπορίου και την επιδείνωση του προβλήματος των πνευματικών δικαιωμάτων στο Διαδίκτυο. Αυτό ισχύει ιδιαίτερα για τις ηλεκτρονικές πωλήσεις προϊόντων πολυμέσων (μουσική, βίντεο, ψηφιακή φωτογραφία κ.λπ.). Με βάση το ντετερμινιστικό χάος, είναι δυνατό να παρέχεται ένας τέτοιος τρόπος για την προστασία των πνευματικών δικαιωμάτων και των δικαιωμάτων πνευματικής ιδιοκτησίας, όπως η μείωση της ποιότητας ενός προϊόντος πληροφοριών όταν είναι διαθέσιμο στο κοινό. Για παράδειγμα, μουσικά κομμάτια που κωδικοποιούνται με χρήση χάους θα διανέμονται στο δίκτυο χωρίς περιορισμούς, ώστε να μπορεί να τα χρησιμοποιήσει κάθε χρήστης. Ωστόσο, όταν ακούτε χωρίς αποκλειστικό αποκωδικοποιητή, η ποιότητα του ήχου θα είναι κακή. Ποιο είναι το νόημα αυτής της προσέγγισης; Οι πληροφορίες που διαδίδονται παραμένουν ανοιχτές και δεν υπόκεινται σε περιορισμούς που επιβάλλονται από τη χρήση μεθόδων κρυπτογραφικής προστασίας. Επιπλέον, ο δυνητικός αγοραστής έχει την ευκαιρία να εξοικειωθεί με το προϊόν και μόνο τότε να αποφασίσει αν θα αγοράσει την έκδοση υψηλής ποιότητας.

Πρέπει να σημειωθεί ότι οι παραπάνω λειτουργίες της χαοτικής κωδικοποίησης δεν εξαντλούν τις πιθανές δυνατότητες εφαρμογής της στις σύγχρονες τεχνολογίες της πληροφορίας. Κατά τη διάρκεια της περαιτέρω μελέτης και ανάπτυξης αυτού του ζητήματος, προφανώς, ενδέχεται να ανοίξουν νέες πτυχές και πολλά υποσχόμενοι τομείς χρήσης.

Έτσι, η χρήση του δυναμικού χάους και των φράκταλ στην τεχνολογία της πληροφορίας δεν είναι εξωτική, όπως φαινόταν μόλις πριν από λίγα χρόνια, αλλά ένας φυσικός τρόπος ανάπτυξης νέων προσεγγίσεων για τη δημιουργία συστημάτων που λειτουργούν αποτελεσματικά σε ένα μεταβαλλόμενο περιβάλλον.

ΘΕΩΡΙΑ ΦΡΑΚΤΑΛ ΚΑΙ ΧΑΟΣ

Ιβάν Τουγκόι

ΕΝΟΤΗΤΑ 1: ΓΕΝΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ

ΤΑ ΦΡΑΚΤΑΛ ΚΑΙ Ο ΚΟΣΜΟΣ ΓΥΡΩ ΜΑΣ

Τα φράκταλ είναι μοναδικά αντικείμενα που δημιουργούνται από τις απρόβλεπτες κινήσεις του χαοτικού κόσμου. Βρίσκονται σε μέρη τόσο μικρά όσο η κυτταρική μεμβράνη και τόσο μεγάλα όσο το ηλιακό σύστημα.

Τα κλαδιά των σωλήνων της τραχείας, τα φύλλα στα δέντρα, οι φλέβες στο χέρι, ένα ποτάμι που βράζει και λυγίζει, το χρηματιστήριο - όλα αυτά είναι φράκταλ. Από τους αρχαίους πολιτισμούς μέχρι τον Μάικλ Τζάκσον, οι επιστήμονες, οι μαθηματικοί και οι καλλιτέχνες, όπως όλοι οι άλλοι σε αυτόν τον πλανήτη, έχουν γοητευτεί από τα φράκταλ και τα χρησιμοποίησαν στη δουλειά τους.

Οι προγραμματιστές και οι επιστήμονες υπολογιστών τρελαίνονται επίσης με τα φράκταλ, καθώς τα φράκταλ άπειρης πολυπλοκότητας και ομορφιάς μπορούν να δημιουργηθούν με απλούς τύπους σε απλούς οικιακούς υπολογιστές. Η ανακάλυψη των φράκταλ ήταν η ανακάλυψη μιας νέας αισθητικής στην τέχνη, την επιστήμη και τα μαθηματικά, καθώς και μια επανάσταση στην ανθρώπινη αντίληψη του κόσμου.

ΤΙ ΕΙΝΑΙ ΠΡΑΓΜΑΤΙΚΑ ΤΑ FRACTAL;

Η λέξη «Fractal» είναι κάτι για το οποίο πολλοί άνθρωποι μιλούν αυτές τις μέρες, από φυσικούς μέχρι μαθητές γυμνασίου. Εμφανίζεται στα εξώφυλλα πολλών εγχειριδίων μαθηματικών, επιστημονικών περιοδικών και κουτιών λογισμικού υπολογιστών. Χρωματιστές εικόνες φράκταλ μπορούν να βρεθούν παντού σήμερα: από καρτ ποστάλ μέχρι μπλουζάκια. Τις τελευταίες δύο δεκαετίες, ο αριθμός των μονάδων προϊόντων που σχετίζονται με φράκταλ που παράγονται ανά μήνα έχει αυξηθεί από αρκετές δεκάδες σε πολλές χιλιάδες!

Λοιπόν, ποια είναι αυτά τα χρωματιστά σχήματα που βλέπουμε παντού γύρω μας; Με απλά λόγια, ένα φράκταλ είναι ένα γεωμετρικό σχήμα, ένα συγκεκριμένο μέρος του οποίου επαναλαμβάνεται ξανά και ξανά, αλλάζει σε μέγεθος. Αυτό ακολουθεί την αρχή της αυτο-ομοιότητας. Όλα τα φράκταλ είναι παρόμοια με τον εαυτό τους, δηλαδή είναι παρόμοια σε όλα τα επίπεδα. Υπάρχουν πολλοί τύποι φράκταλ και ένας αρκετά μεγάλος αριθμός από αυτούς περιγράφεται εδώ.

Ωστόσο, τα φράκταλ δεν είναι απλώς σύνθετα στοιχεία που παράγονται από υπολογιστές. Οτιδήποτε φαίνεται τυχαίο και ακανόνιστο θα μπορούσε να είναι φράκταλ. Θεωρητικά, μπορούμε να πούμε ότι ό,τι υπάρχει στον πραγματικό κόσμο είναι φράκταλ, είτε είναι σύννεφο είτε ένα μικρό μόριο οξυγόνου.

ΠΟΣΟ ΧΑΟΤΙΚΟ ΕΙΝΑΙ ΤΟ ΧΑΟΣ;

Τα φράκταλ συνδέονται πάντα με τη λέξη χάος. Προσωπικά θα όριζα τα φράκταλ ως σωματίδια χάους. Τα φράκταλ παρουσιάζουν χαοτική συμπεριφορά που τα κάνει να φαίνονται τόσο άτακτα και τυχαία. Αλλά αν κοιτάξετε αρκετά προσεκτικά, μπορείτε να δείτε πολλές πτυχές της αυτο-ομοιότητας μέσα στο φράκταλ. Για παράδειγμα, κοιτάξτε ένα δέντρο, επιλέξτε ένα συγκεκριμένο κλαδί και μελετήστε το πιο προσεκτικά. Τώρα επιλέξτε ένα μάτσο από πολλά φύλλα. Για τους φράκταλ επιστήμονες (που μερικές φορές αποκαλούνται χαολόγοι), και τα τρία αυτά αντικείμενα φαίνονται πανομοιότυπα.

Η λέξη χάος κάνει τους περισσότερους να σκεφτούν κάτι χαοτικό και απρόβλεπτο. Στην πραγματικότητα αυτό δεν είναι αλήθεια. Πόσο χαοτικό είναι λοιπόν το χάος; Η απάντηση είναι ότι το χάος είναι, στην πραγματικότητα, αρκετά τακτοποιημένο και υπακούει σε ορισμένους νόμους. Το πρόβλημα είναι ότι η εύρεση αυτών των νόμων μπορεί να είναι πολύ δύσκολη. Ο στόχος της μελέτης του χάους και των φράκταλ είναι η πρόβλεψη μοτίβων σε συστήματα που μπορεί να φαίνονται απρόβλεπτα και εντελώς χαοτικά.

Ένα σύστημα είναι μια συλλογή πραγμάτων ή μια περιοχή μελέτης και μερικά από τα κοινά συστήματα που θέλουν να μελετήσουν οι χαολόγοι περιλαμβάνουν σχηματισμούς νεφών, καιρικές συνθήκες, κινήσεις νερού, μεταναστεύσεις ζώων και πολλές άλλες πτυχές της ζωής της Μητέρας Φύσης. Άρα, τελικά, ίσως όλος ο κόσμος γύρω μας να είναι φράκταλ!

ΓΕΩΜΕΤΡΙΑ ΤΟΥ 21ου ΑΙΩΝΑ

Για πολλούς χαολόγους, η μελέτη του χάους και των φράκταλ δεν είναι απλώς ένα νέο πεδίο γνώσης που συνδυάζει μαθηματικά, θεωρητική φυσική, τέχνη και τεχνολογία υπολογιστών - είναι μια επανάσταση. Αυτή είναι η ανακάλυψη ενός νέου τύπου γεωμετρίας, της γεωμετρίας που περιγράφει τον κόσμο γύρω μας και που μπορεί να δει κανείς όχι μόνο στα σχολικά βιβλία, αλλά και στη φύση και παντού στο απεριόριστο σύμπαν.

Ο πρωτοπόρος σε αυτό το νέο πεδίο γνώσης, τον οποίο πολλοί αποκαλούν πατέρα των φράκταλ, ήταν ο Γαλλοαμερικανός μαθηματικός καθηγητής Benoit B. Mandelbrot. Στα μέσα της δεκαετίας του 1960, μετά από δεκαετίες μελέτης και έρευνας, ο Mandelbrot ανέπτυξε αυτό που ονόμασε fractal geometry ή γεωμετρία της φύσης (για το οποίο έγραψε το βιβλίο του με τις μεγαλύτερες πωλήσεις, Fractal Geometry of Nature). Ο σκοπός της γεωμετρίας φράκταλ ήταν να αναλύσει σπασμένα, ζαρωμένα και ασαφή σχήματα. Ο Mandelbrot χρησιμοποίησε τη λέξη φράκταλ επειδή υποδήλωνε κατακερματισμό και φραξιονισμό σε αυτές τις μορφές.

Σήμερα, ο Mandelbrot και άλλοι επιστήμονες όπως ο Clifford A. Pickover, ο James Gleick ή ο H.O. Peitgen προσπαθούν να επεκτείνουν το πεδίο της γεωμετρίας φράκταλ έτσι ώστε να μπορεί να εφαρμοστεί σχεδόν σε οτιδήποτε στον κόσμο, από την πρόβλεψη τιμών στην αγορά χρεογράφων μέχρι τη δημιουργία νέων ανακαλύψεις στη θεωρητική φυσική.

ΠΡΑΚΤΙΚΗ ΕΦΑΡΜΟΓΗ ΦΡΑΚΤΑΛ

Τα φράκταλ βρίσκουν όλο και περισσότερες εφαρμογές στην επιστήμη. Ο κύριος λόγος για αυτό είναι ότι περιγράφουν τον πραγματικό κόσμο μερικές φορές ακόμη καλύτερα από την παραδοσιακή φυσική ή τα μαθηματικά. Να μερικά παραδείγματα:

ΥΠΟΛΟΓΙΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ

Η πιο χρήσιμη χρήση των φράκταλ στην επιστήμη των υπολογιστών είναι η συμπίεση δεδομένων φράκταλ. Αυτός ο τύπος συμπίεσης βασίζεται στο γεγονός ότι ο πραγματικός κόσμος περιγράφεται καλά από τη γεωμετρία φράκταλ. Ταυτόχρονα, οι εικόνες συμπιέζονται πολύ καλύτερα από ότι γίνεται με συμβατικές μεθόδους (όπως jpeg ή gif). Ένα άλλο πλεονέκτημα της συμπίεσης φράκταλ είναι ότι όταν η εικόνα μεγεθύνεται, δεν υπάρχει αποτέλεσμα pixelation (αύξηση του μεγέθους των κουκκίδων σε μεγέθη που παραμορφώνουν την εικόνα). Με τη συμπίεση φράκταλ, μετά τη μεγέθυνση, η εικόνα συχνά φαίνεται ακόμα καλύτερη από πριν.

ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ

Η μελέτη των αναταράξεων στις ροές προσαρμόζεται πολύ καλά στα φράκταλ. Οι τυρβώδεις ροές είναι χαοτικές και επομένως είναι δύσκολο να μοντελοποιηθούν με ακρίβεια. Και εδώ βοηθά η μετάβαση σε μια αναπαράσταση φράκταλ, η οποία διευκολύνει πολύ το έργο των μηχανικών και των φυσικών, επιτρέποντάς τους να κατανοήσουν καλύτερα τη δυναμική των πολύπλοκων ροών.

Χρησιμοποιώντας φράκταλ μπορείτε επίσης να προσομοιώσετε φλόγες.

Τα πορώδη υλικά αντιπροσωπεύονται καλά σε φράκταλ μορφή λόγω του γεγονότος ότι έχουν πολύ περίπλοκη γεωμετρία. Χρησιμοποιείται στην επιστήμη των πετρελαιοειδών.

ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ

Για τη μετάδοση δεδομένων σε αποστάσεις χρησιμοποιούνται κεραίες με σχήματα φράκταλ, γεγονός που μειώνει σημαντικά το μέγεθος και το βάρος τους.

ΦΥΣΙΚΗ ΕΠΙΦΑΝΕΙΩΝ

Τα φράκταλ χρησιμοποιούνται για να περιγράψουν την καμπυλότητα των επιφανειών. Μια ανώμαλη επιφάνεια χαρακτηρίζεται από συνδυασμό δύο διαφορετικών φράκταλ.

ΦΑΡΜΑΚΟ

Βιοαισθητηριακές αλληλεπιδράσεις

ΧΤΥΠΟΣ καρδιας

ΒΙΟΛΟΓΙΑ

Μοντελοποίηση χαοτικών διαδικασιών, ιδιαίτερα κατά την περιγραφή μοντέλων πληθυσμού.

ΦΡΑΚΤΑΛ ΔΙΑΣΤΑΣΗ: ΚΡΥΦΕΣ ΔΙΑΣΤΑΣΕΙΣ

Μια από τις ιδέες που προέκυψαν από την ανακάλυψη της γεωμετρίας φράκταλ ήταν η ιδέα των μη ακέραιων τιμών για τον αριθμό των διαστάσεων στο χώρο. Φυσικά, δεν μπορούμε να κατανοήσουμε τετραδιάστατα πράγματα, αν και ο Lucky Tesseract εργάζεται ενεργά προς αυτή την κατεύθυνση. Ο Mandelbrot ονόμασε μη ακέραιες διαστάσεις όπως διαστάσεις φράκταλ 2,76. Η συνηθισμένη ευκλείδεια γεωμετρία δηλώνει ότι ο χώρος είναι ομαλός και επίπεδος. Οι ιδιότητες ενός τέτοιου χώρου ορίζονται από σημεία, γραμμές, γωνίες, τρίγωνα, κύβους, σφαίρες, τετράεδρα κ.λπ.

Ο Mandelbrot πίστευε ότι το πραγματικό τοπίο του διαστήματος δεν είναι επίπεδο και ότι στον κόσμο μας δεν υπάρχει τίποτα που να είναι εντελώς επίπεδο, στρογγυλό, δηλαδή όλα να είναι φράκταλ. Επομένως, ένα αντικείμενο που έχει ακριβώς 3 διαστάσεις είναι αδύνατο. Αυτός είναι ο λόγος για τον οποίο χρειαζόταν η έννοια της διάστασης φράκταλ για να μετρηθεί ο βαθμός στον οποίο τα πράγματα είναι τραχιά.

Για παράδειγμα, κοιτάξτε ένα κομμάτι χαρτί (υποθέτοντας ότι είναι δισδιάστατο) τσαλακωμένο σε μπάλα. Είναι δισδιάστατος; Όχι, γιατί έχει μήκος, πλάτος και ύψος. Δεν μπορεί όμως να είναι και τρισδιάστατο, γιατί είναι φτιαγμένο από ένα απείρως λεπτό φύλλο και, επιπλέον, δεν είναι εντελώς ομοιογενές. Άρα, η φράκταλ διάστασή του είναι περίπου 2,5. Αλλά η κανονική του διάσταση, που ονομάζεται επίσης Ευκλείδεια διάσταση, θα είναι ίση με 3. Όλα τα φράκταλ, ειδικά οι φράκταλ καμπύλες, έχουν φράκταλ διαστάσεις. Ο Mandelbrot χρησιμοποιούσε συχνά το παράδειγμα ότι η ακτογραμμή της Αγγλίας ήταν άπειρου μήκους.

Δοκιμάστε να εντοπίσετε την ακτογραμμή της Αγγλίας σε έναν άτλαντα. Στη συνέχεια κάντε το ίδιο με τον ναυτικό χάρτη. Παραδόξως, η τιμή της τελευταίας μέτρησης θα είναι πολύ μεγαλύτερη. Στη συνέχεια, πηγαίνετε στην Αγγλία και μετρήστε την ακτογραμμή της με ένα μέτρο ράφι. Αυτό το μήκος θα είναι ακόμη μεγαλύτερο. Συνεχίστε αυτή τη διαδικασία μέχρι να έχετε στα χέρια σας έναν χάρακα σχεδίασης με τον οποίο μπορείτε να μετρήσετε την ακτογραμμή, σωματίδιο με σωματίδιο, άτομο προς άτομο. Φυσικά η ιδέα πίσω από αυτό το μη πρακτικό πείραμα είναι ότι οι αποστάσεις πρέπει να είναι συγκρίσιμες σε κλίμακα, θέση και λεπτομέρεια. Ο Mandelbrot αργότερα προσδιόρισε ότι η διάσταση φράκταλ της αγγλικής ακτογραμμής ήταν 1,25.

Πολλά αντικείμενα στη φύση (για παράδειγμα, το ανθρώπινο σώμα) αποτελούνται από πολλά φράκταλ αναμεμειγμένα μεταξύ τους και κάθε φράκταλ έχει τη δική του διάσταση διαφορετική από τις διαστάσεις των άλλων. Για παράδειγμα, η δισδιάστατη επιφάνεια του ανθρώπινου αγγειακού συστήματος κάμπτεται, διακλαδίζεται, συστρέφεται και συστέλλεται έτσι ώστε η φράκταλ διάστασή της να είναι 3,0. Αν όμως χωριζόταν σε ξεχωριστά μέρη, η φράκταλ διάσταση των αρτηριών θα ήταν μόνο 2,7, ενώ οι βρογχικές διόδους στους πνεύμονες θα είχαν φράκταλ διάσταση 1,07.

ΕΝΟΤΗΤΑ 2: ΝΤΕΤΕΜΙΝΙΣΤΙΚΑ ΦΡΑΚΤΑΛ

ΓΕΝΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ

Τα πρώτα φράκταλ που ανακαλύφθηκαν ήταν τα λεγόμενα. ντετερμινιστικά φράκταλ. Το ιδιαίτερο χαρακτηριστικό τους είναι η ιδιότητα της αυτοομοιότητας, λόγω των ιδιαιτεροτήτων της μεθόδου της παραγωγής τους.

Μερικοί προτιμούν να ονομάζουν αυτά τα φράκταλ κλασικά, γεωμετρικά φράκταλ ή γραμμικά φράκταλ. Αυτά τα φράκταλ συνήθως σχηματίζονται ξεκινώντας με έναν εκκινητή - ένα σχήμα στο οποίο εφαρμόζεται ένα συγκεκριμένο υποκείμενο σχέδιο. Σε όλα τα ντετερμινιστικά φράκταλ, η αυτο-ομοιότητα εμφανίζεται σε όλα τα επίπεδα. Αυτό σημαίνει ότι όσο και να κάνετε μεγέθυνση στο φράκταλ, θα εξακολουθείτε να βλέπετε το ίδιο μοτίβο. Για σύνθετα φράκταλ, τα οποία θα συζητηθούν αργότερα, αυτό δεν ισχύει. Τα ντετερμινιστικά φράκταλ σχηματίζονται μέσω μιας διαδικασίας που ονομάζεται επανάληψη, η οποία εφαρμόζει ένα βασικό μοτίβο σε έναν εκκινητή, στη συνέχεια το εφαρμόζει σε ένα αποτέλεσμα και ούτω καθεξής. Οι περισσότεροι άνθρωποι επαναλαμβάνουν ντετερμινιστικά φράκταλ 5-7 φορές για να έχουν μια καθαρή, όμορφη εικόνα. Αυτά τα φράκταλ είναι γραμμικά, γιατί σε κάθε επανάληψη, κάτι αφαιρείται ή προστίθεται με τη μορφή ευθειών. Παρακάτω είναι παραδείγματα μερικών κοινών ντετερμινιστικών φράκταλ που δημιουργούνται σε έναν κανονικό υπολογιστή χρησιμοποιώντας απλά προγράμματα BASIC.

ΣΙΕΠΙΝΣΚΙ ΠΛΕΓΜΑ

Αυτό είναι ένα από τα φράκταλ με τα οποία πειραματίστηκε ο Mandelbrot όταν ανέπτυξε τις έννοιες των διαστάσεων και των επαναλήψεων φράκταλ. Τρίγωνα που σχηματίζονται συνδέοντας τα μέσα ενός μεγαλύτερου τριγώνου κόβονται από το κύριο τρίγωνο, σχηματίζοντας ένα τρίγωνο με περισσότερες τρύπες. Σε αυτή την περίπτωση, ο εκκινητής είναι το μεγάλο τρίγωνο και το πρότυπο είναι η λειτουργία κοπής τριγώνων παρόμοια με το μεγαλύτερο. Μπορείτε επίσης να αποκτήσετε μια τρισδιάστατη εκδοχή ενός τριγώνου χρησιμοποιώντας ένα συνηθισμένο τετράεδρο και κόβοντας μικρά τετράεδρα. Η διάσταση ενός τέτοιου φράκταλ είναι ln3/ln2 = 1,584962501.

Για να πάρετε ένα χαλί Sierpinski, πάρτε ένα τετράγωνο, χωρίστε το σε εννέα τετράγωνα και κόψτε το μεσαίο. Το ίδιο θα κάνουμε και με τα υπόλοιπα, μικρότερα τετράγωνα. Τελικά, σχηματίζεται ένα επίπεδο πλέγμα φράκταλ, χωρίς εμβαδόν αλλά με άπειρες συνδέσεις. Στη χωρική του μορφή, το σφουγγάρι Sierpinski μετατρέπεται σε ένα σύστημα μορφών από άκρο σε άκρο, στο οποίο κάθε στοιχείο από άκρο σε άκρο αντικαθίσταται συνεχώς από το δικό του είδος. Αυτή η δομή μοιάζει πολύ με ένα τμήμα οστικού ιστού. Κάποτε τέτοιες επαναλαμβανόμενες κατασκευές θα γίνουν στοιχείο κτιριακών κατασκευών. Η στατικότητα και η δυναμική τους, πιστεύει ο Mandelbrot, αξίζουν προσεκτικής μελέτης.

SIERPINSKI FRACTAL

Μην συγχέετε αυτό το φράκταλ με το πλέγμα Sierpinski. Πρόκειται για δύο εντελώς διαφορετικά αντικείμενα. Σε αυτό το φράκταλ, ο εκκινητής και η γεννήτρια είναι τα ίδια. Σε κάθε επανάληψη, ένα μικρότερο αντίγραφο του εκκινητή προστίθεται σε κάθε γωνία της γεννήτριας και ούτω καθεξής. Εάν εκτελούνταν άπειρος αριθμός επαναλήψεων κατά τη δημιουργία αυτού του φράκταλ, θα καταλάμβανε ολόκληρο το επίπεδο, χωρίς να αφήσει ούτε μια τρύπα. Επομένως, η φράκταλ διάστασή του ln9/ln3 = 2,0

ΚΑΜΠΥΛΗ KOCH

Η καμπύλη Koch είναι ένα από τα πιο τυπικά ντετερμινιστικά φράκταλ. Εφευρέθηκε τον δέκατο ένατο αιώνα από έναν Γερμανό μαθηματικό ονόματι Helge von Koch, ο οποίος, ενώ μελετούσε το έργο του Georg Kontor και του Karl Weierstrasse, συνάντησε περιγραφές κάποιων περίεργων καμπυλών με ασυνήθιστη συμπεριφορά. Ο εκκινητής είναι μια ευθεία γραμμή. Η γεννήτρια είναι ένα ισόπλευρο τρίγωνο, οι πλευρές του οποίου είναι ίσες με το ένα τρίτο του μήκους του μεγαλύτερου τμήματος. Αυτά τα τρίγωνα προστίθενται στο μέσο κάθε τμήματος ξανά και ξανά. Στην έρευνά του, ο Mandelbrot πειραματίστηκε εκτενώς με τις καμπύλες Koch και παρήγαγε φιγούρες όπως νησιά Koch, Koch Crosses, Koch Snowflakes, ακόμα και τρισδιάστατες αναπαραστάσεις της καμπύλης Koch χρησιμοποιώντας ένα τετράεδρο και προσθέτοντας μικρότερα τετράεδρα σε κάθε όψη της. Η καμπύλη Koch έχει διάσταση ln4/ln3 = 1,261859507.

Ο σταυρός Koch είναι μια παραλλαγή της καμπύλης Koch που εφευρέθηκε από τον Mandelbrot. Αντί για ευθύγραμμο τμήμα, χρησιμοποίησε ένα τετράγωνο ή ορθογώνιο ως εκκινητή. Εφόσον αυτό το φράκταλ χρησιμοποιεί την ίδια ιδέα με την αρχική καμπύλη Koch, η φράκταλ διάστασή του είναι η ίδια: ln4/ln3 = 1,261859507.

ΜΑΝΤΕΛΜΠΡΟΤ ΦΡΑΚΤΑΛ

Αυτό ΔΕΝ είναι το σετ Mandelbrot, το οποίο βλέπετε αρκετά συχνά. Το σύνολο Mandelbrot βασίζεται σε μη γραμμικές εξισώσεις και είναι ένα σύνθετο φράκταλ. Αυτή είναι επίσης μια παραλλαγή της καμπύλης Koch, αν και αυτό το αντικείμενο δεν είναι παρόμοιο με αυτήν. Ο εκκινητής και η γεννήτρια είναι επίσης διαφορετικά από αυτά που χρησιμοποιούνται για τη δημιουργία φράκταλ με βάση την αρχή της καμπύλης Koch, αλλά η ιδέα παραμένει η ίδια. Αντί να ενώνονται ισόπλευρα τρίγωνα σε ένα τμήμα καμπύλης, τα τετράγωνα ενώνονται με ένα τετράγωνο. Λόγω του γεγονότος ότι αυτό το φράκταλ καταλαμβάνει ακριβώς το μισό του εκχωρημένου χώρου σε κάθε επανάληψη, έχει μια απλή διάσταση φράκταλ 3/2 = 1,5

FRACTALS ΑΣΤΕΡΙ ΚΑΙ ΧΙΟΝΙΦΑΝΑ

Και τα δύο αυτά αντικείμενα δεν είναι κλασικά φράκταλ και δεν εφευρέθηκαν από τον Mandelbrot ή οποιονδήποτε άλλο διάσημο μαθηματικό. Απλώς δημιούργησα αυτά τα φράκταλ από ενδιαφέρον και για να πειραματιστώ με τον προγραμματισμό. Τόσο ο εκκινητής όσο και η γεννήτρια εδώ είναι ένα σχήμα που σχηματίζεται συνδέοντας τα μέσα των πλευρών με τα μέσα των απέναντι πλευρών σε ένα κανονικό εξάγωνο. Επιπλέον, μπορώ μόνο να υποψιάζομαι τη διάσταση αυτών των φράκταλ.

ΛΟΥΚΑΝΙΚΟ MINKOWSKI

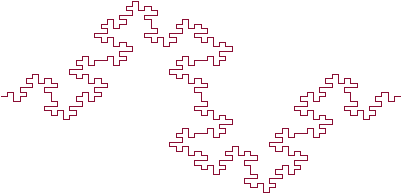
Ο συγγραφέας αυτού του φράκταλ είναι ο Herman Minkowski, από τον οποίο πήρε το όνομά του. Ο Minkowski δεν πρότεινε τον όρο λουκάνικο για να ονομάσει αυτό το αντικείμενο. Η λέξη curve ή απλώς φράκταλ μπορεί να ήταν πιο ελκυστική. Τόσο ο εκκινητής όσο και η γεννήτρια είναι αρκετά περίπλοκοι και αποτελούνται από έναν αριθμό ορθών γωνιών και τμημάτων ποικίλου μήκους. Ο ίδιος ο εμπνευστής έχει 8 μέρη. Φράκταλ διάσταση λουκάνικου Minkowski - ln8/ln4 = 1,5

FRACTAL ΛΑΒΥΡΙΝΘΟΣ

Αυτό το φράκταλ ονομάζεται μερικές φορές και H-tree. Τόσο ο εκκινητής όσο και η γεννήτρια έχουν σχήμα όπως το γράμμα H. Στο παράδειγμα που φαίνεται εδώ, το ίδιο το H δεν είναι σκιασμένο. Αντίθετα, οι περιοχές έξω από το φράκταλ γεμίζουν, καθιστώντας το σχέδιο και το σχέδιο πιο εύκολα αντιληπτά. Η διάσταση φράκταλ του συγκεκριμένου φράκταλ είναι αρκετά ενδιαφέρουσα. Δεδομένου ότι το πάχος του H μειώνεται κατά την επανάληψη, η διάσταση των άκρων του γράμματος H είναι ακριβώς 2,0, αλλά τα στοιχεία μεταξύ των άκρων έχουν διαφορετική διάσταση, που κυμαίνεται από 1,3333 έως 1,6667.

ΠΕΡΙΣΣΟΤΕΡΟ ΠΕΝΤΑΓΚΟΝΙ

Ένα φράκταλ μοιάζει με ένα μάτσο πεντάγωνα συμπιεσμένα μεταξύ τους. Στην πραγματικότητα, σχηματίζεται χρησιμοποιώντας ένα πεντάγωνο ως εκκινητή και ισοσκελές τρίγωνα στα οποία η αναλογία της μεγαλύτερης προς τη μικρότερη πλευρά είναι ακριβώς ίση με τη λεγόμενη χρυσή αναλογία (1,618033989 ή 1/(2cos72)) ως γεννήτρια. . Αυτά τα τρίγωνα κόβονται από τη μέση κάθε πενταγώνου, με αποτέλεσμα ένα σχήμα που μοιάζει με 5 μικρά πεντάγωνα κολλημένα σε ένα μεγάλο.

Μια παραλλαγή αυτού του φράκταλ μπορεί να ληφθεί χρησιμοποιώντας ένα εξάγωνο ως εκκινητή. Αυτό το φράκταλ ονομάζεται το αστέρι του Δαβίδ και μοιάζει αρκετά με μια εξαγωνική εκδοχή της νιφάδας χιονιού Koch. Η φράκταλ διάσταση του πενταγώνου Darer είναι ln6/ln(1+g), όπου g είναι ο λόγος του μήκους της μεγαλύτερης πλευράς του τριγώνου προς το μήκος της μικρότερης. Σε αυτήν την περίπτωση, το g είναι η Χρυσή Αναλογία, επομένως η διάσταση του φράκταλ είναι περίπου 1,86171596. Φράκταλ διάσταση του Άστρου του Δαβίδ ln6/ln3 ή 1,630929754.

ΚΑΜΠΥΛΗ ΔΡΑΚΟΥ

Εφευρέθηκε από τον Ιταλό μαθηματικό Giuseppe Peano, το Dragon Curve, ή Dragon Sweep όπως το ονόμασε, μοιάζει πολύ με ένα λουκάνικο Minkowski. Χρησιμοποιήθηκε ένας απλούστερος εκκινητής και η γεννήτρια ήταν η ίδια. Ο Mandelbrot ονόμασε αυτό το φράκταλ Ποταμός Double Dragon. Η φράκταλ διάστασή του είναι περίπου 1,5236.

HILBERT CURVE

Αυτό το φράκταλ μοιάζει πολύ με το Φράκταλ του Λαβύρινθου, εκτός από το γεγονός ότι το πλάτος του γράμματος U, που είναι η γεννήτρια, δεν αλλάζει με κάθε επανάληψη. Ωστόσο, σε αντίθεση με το Φράκταλ του Λαβύρινθου, η καμπύλη Hilbert, που ονομάζεται επίσης Ξενοδοχείο Χίλμπερτ, έχει μια ενιαία διάσταση φράκταλ, η οποία είναι ακριβώς 2,0, αφού με άπειρο αριθμό επαναλήψεων, θα καταλάβει ολόκληρο το επίπεδο.

FRACTAL BOX

Αυτό είναι ένα πολύ απλό ντετερμινιστικό φράκταλ που σχηματίζεται με την προσθήκη τετραγώνων στις κορυφές άλλων τετραγώνων. Και ο εκκινητής και η γεννήτρια είναι τετράγωνα. Η φράκταλ διάστασή του είναι ln8/ln3 ή 1,892789261.

ΕΝΟΤΗΤΑ 3: ΣΥΝΘΕΤΑ ΦΡΑΚΤΑΛ

ΓΕΝΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ

Τα περισσότερα φράκταλ που βρίσκονται σήμερα δεν είναι ντετερμινιστικά. Δεν είναι γραμμικά και δεν συναρμολογούνται από επαναλαμβανόμενα γεωμετρικά σχήματα. Τέτοια φράκταλ ονομάζονται σύνθετα.

Στην πραγματικότητα, εάν μεγεθύνετε μια μικρή περιοχή οποιουδήποτε πολύπλοκου φράκταλ και στη συνέχεια κάνετε το ίδιο με μια μικρή περιοχή αυτής της περιοχής, οι δύο μεγεθύνσεις θα διαφέρουν σημαντικά μεταξύ τους. Οι δύο εικόνες θα μοιάζουν πολύ στη λεπτομέρεια, αλλά δεν θα είναι εντελώς πανομοιότυπες.

Συγκρίνετε, για παράδειγμα, τις εικόνες του σετ Mandelbrot που εμφανίζονται εδώ, η μία από τις οποίες λήφθηκε με τη μεγέθυνση μιας συγκεκριμένης περιοχής της άλλης. Όπως μπορείτε να δείτε, δεν είναι απολύτως πανομοιότυπα, αν και και στα δύο βλέπουμε έναν μαύρο κύκλο, από τον οποίο φλεγόμενα πλοκάμια εκτείνονται σε διαφορετικές κατευθύνσεις. Αυτά τα στοιχεία επαναλαμβάνονται επ' αόριστον στο σύνολο Mandelbrot σε φθίνουσες αναλογίες.

Τα ντετερμινιστικά φράκταλ είναι γραμμικά, ενώ τα σύνθετα φράκταλ όχι. Όντας μη γραμμικά, αυτά τα φράκταλ δημιουργούνται από αυτό που ο Mandelbrot ονόμασε μη γραμμικές αλγεβρικές εξισώσεις. Ένα καλό παράδειγμα είναι η διαδικασία Zn+1=ZnI + C, η οποία είναι η εξίσωση που χρησιμοποιείται για την κατασκευή του συνόλου Mandelbrot και Julia του δεύτερου βαθμού. Η επίλυση αυτών των μαθηματικών εξισώσεων περιλαμβάνει μιγαδικούς και φανταστικούς αριθμούς. Όταν η εξίσωση ερμηνεύεται γραφικά στο μιγαδικό επίπεδο, το αποτέλεσμα είναι ένα περίεργο σχήμα στο οποίο οι ευθείες γραμμές γίνονται καμπύλες και εμφανίζονται φαινόμενα αυτο-ομοιότητας, αν και όχι χωρίς παραμορφώσεις, σε διάφορα επίπεδα κλίμακας. Ταυτόχρονα, η όλη εικόνα στο σύνολό της είναι απρόβλεπτη και πολύ χαοτική.

Όπως μπορείτε να δείτε κοιτάζοντας τις εικόνες, τα σύνθετα φράκταλ είναι πράγματι πολύ περίπλοκα και δεν μπορούν να δημιουργηθούν χωρίς τη βοήθεια υπολογιστή. Για να αποκτήσετε πολύχρωμα αποτελέσματα, αυτός ο υπολογιστής πρέπει να διαθέτει έναν ισχυρό μαθηματικό συνεπεξεργαστή και μια οθόνη υψηλής ανάλυσης. Σε αντίθεση με τα ντετερμινιστικά φράκταλ, τα σύνθετα φράκταλ δεν υπολογίζονται σε 5-10 επαναλήψεις. Σχεδόν κάθε σημείο στην οθόνη ενός υπολογιστή είναι σαν ένα ξεχωριστό φράκταλ. Κατά τη μαθηματική επεξεργασία, κάθε σημείο αντιμετωπίζεται ως ξεχωριστό σχέδιο. Κάθε σημείο αντιστοιχεί σε μια συγκεκριμένη τιμή. Η εξίσωση είναι ενσωματωμένη για κάθε σημείο και εκτελείται, για παράδειγμα, 1000 επαναλήψεις. Για να αποκτήσετε μια σχετικά μη παραμορφωμένη εικόνα σε μια χρονική περίοδο αποδεκτή για οικιακούς υπολογιστές, είναι δυνατό να πραγματοποιήσετε 250 επαναλήψεις για ένα σημείο.

Τα περισσότερα από τα φράκταλ που βλέπουμε σήμερα είναι όμορφα χρωματισμένα. Ίσως οι εικόνες φράκταλ αποκτούν τόσο μεγάλη αισθητική σημασία ακριβώς λόγω των χρωμάτων τους. Αφού υπολογιστεί η εξίσωση, ο υπολογιστής αναλύει τα αποτελέσματα. Εάν τα αποτελέσματα παραμένουν σταθερά ή κυμαίνονται γύρω από μια συγκεκριμένη τιμή, η κουκκίδα συνήθως γίνεται μαύρη. Εάν η τιμή σε ένα ή άλλο βήμα τείνει στο άπειρο, το σημείο βάφεται με διαφορετικό χρώμα, ίσως μπλε ή κόκκινο. Κατά τη διάρκεια αυτής της διαδικασίας, ο υπολογιστής εκχωρεί χρώματα σε όλες τις ταχύτητες κίνησης.

Συνήθως, οι κουκκίδες που κινούνται γρήγορα έχουν κόκκινο χρώμα, ενώ οι πιο αργές έχουν κίτρινο χρώμα και ούτω καθεξής. Τα σκοτεινά σημεία είναι ίσως τα πιο σταθερά.

Τα σύνθετα φράκταλ διαφέρουν από τα ντετερμινιστικά φράκταλ με την έννοια ότι είναι απείρως πολύπλοκα, αλλά μπορούν ακόμα να δημιουργηθούν με έναν πολύ απλό τύπο. Τα ντετερμινιστικά φράκταλ δεν απαιτούν τύπους ή εξισώσεις. Απλώς πάρτε λίγο χαρτί σχεδίασης και μπορείτε να φτιάξετε ένα κόσκινο Sierpinski έως και 3 ή 4 επαναλήψεις χωρίς καμία δυσκολία. Δοκιμάστε αυτό με πολλά Julia! Είναι πιο εύκολο να μετρήσετε το μήκος της ακτογραμμής της Αγγλίας!

ΣΕΤ MANDELBROT

Τα σετ Mandelbrot και Julia είναι πιθανώς τα δύο πιο κοινά μεταξύ των πολύπλοκων φράκταλ. Μπορούν να βρεθούν σε πολλά επιστημονικά περιοδικά, εξώφυλλα βιβλίων, καρτ ποστάλ και προφύλαξη οθόνης υπολογιστών. Το σετ Mandelbrot, το οποίο κατασκευάστηκε από τον Benoit Mandelbrot, είναι ίσως ο πρώτος συσχετισμός που έχουν οι άνθρωποι όταν ακούν τη λέξη φράκταλ. Αυτό το φράκταλ, που μοιάζει με μηχανή λαναρίσματος με φλεγόμενα δέντρα και κυκλικές περιοχές προσαρτημένες σε αυτό, δημιουργείται από τον απλό τύπο Zn+1=Zna+C, όπου τα Z και C είναι μιγαδικοί αριθμοί και ο a είναι θετικός αριθμός.

Το σύνολο Mandelbrot, το οποίο μπορεί να δει κανείς πιο συχνά, είναι το σύνολο Mandelbrot του 2ου βαθμού, δηλαδή a = 2. Το γεγονός ότι το σύνολο Mandelbrot δεν είναι μόνο Zn+1=ZnІ+C, αλλά ένα φράκταλ, ο δείκτης στον τύπο του οποίου μπορεί να είναι οποιοσδήποτε θετικός αριθμός, έχει παραπλανήσει πολλούς. Σε αυτή τη σελίδα βλέπετε ένα παράδειγμα του συνόλου Mandelbrot για διάφορες τιμές του εκθέτη a.

Η διαδικασία Z=Z*tg(Z+C) είναι επίσης δημοφιλής. Συμπεριλαμβάνοντας τη συνάρτηση εφαπτομένης, το αποτέλεσμα είναι ένα σύνολο Mandelbrot που περιβάλλεται από μια περιοχή που μοιάζει με μήλο. Κατά τη χρήση της συνημίτονος, επιτυγχάνονται εφέ φυσαλίδων αέρα. Εν ολίγοις, υπάρχει άπειρος αριθμός τρόπων για να διαμορφώσετε το σύνολο Mandelbrot ώστε να δημιουργεί διαφορετικές όμορφες εικόνες.

ΠΟΛΛΗ ΤΖΟΥΛΙΑ

Παραδόξως, τα σετ Julia διαμορφώνονται σύμφωνα με τον ίδιο τύπο με το σετ Mandelbrot. Το σετ Julia επινοήθηκε από τον Γάλλο μαθηματικό Gaston Julia, από τον οποίο ονομάστηκε το σετ. Το πρώτο ερώτημα που προκύπτει μετά από μια οπτική γνωριμία με τα σύνολα Mandelbrot και Julia είναι "αν και τα δύο φράκταλ δημιουργούνται σύμφωνα με τον ίδιο τύπο, γιατί είναι τόσο διαφορετικά;" Πρώτα δείτε τις φωτογραφίες του σετ Julia. Παραδόξως, υπάρχουν διαφορετικοί τύποι σετ Julia. Όταν σχεδιάζετε ένα φράκταλ χρησιμοποιώντας διαφορετικά σημεία εκκίνησης (για να ξεκινήσετε τη διαδικασία επανάληψης), δημιουργούνται διαφορετικές εικόνες. Αυτό ισχύει μόνο για το σετ Julia:

Αν και δεν φαίνεται στην εικόνα, ένα φράκταλ Mandelbrot είναι στην πραγματικότητα πολλά φράκταλ Julia που συνδέονται μεταξύ τους. Κάθε σημείο (ή συντεταγμένη) του συνόλου Mandelbrot αντιστοιχεί σε ένα φράκταλ Julia. Τα σύνολα Julia μπορούν να δημιουργηθούν χρησιμοποιώντας αυτά τα σημεία ως αρχικές τιμές στην εξίσωση Z=ZI+C. Αλλά αυτό δεν σημαίνει ότι εάν επιλέξετε ένα σημείο στο φράκταλ Mandelbrot και το μεγεθύνετε, μπορείτε να πάρετε το φράκταλ Julia. Αυτά τα δύο σημεία είναι πανομοιότυπα, αλλά μόνο με μαθηματική έννοια. Εάν λάβετε αυτό το σημείο και το υπολογίσετε χρησιμοποιώντας αυτόν τον τύπο, μπορείτε να πάρετε ένα φράκταλ Julia που αντιστοιχεί σε ένα ορισμένο σημείο του φράκταλ Mandelbrot.

ΕΝΟΤΗΤΑ 4: ΘΕΩΡΙΑ ΧΑΟΣ

ΤΙ ΕΙΝΑΙ Η ΘΕΩΡΙΑ ΧΑΟΣ;

Τυπικά, η θεωρία του χάους ορίζεται ως η μελέτη πολύπλοκων μη γραμμικών δυναμικών συστημάτων. Αυτό εννοείται με τον όρο μιγαδικό, και με τον όρο μη γραμμικό εννοούμε αναδρομή και αλγόριθμους από ανώτερα μαθηματικά και, τέλος, δυναμικό σημαίνει μη σταθερό και μη περιοδικό. Ετσι, θεωρία του χάους είναι η μελέτη των συνεχώς μεταβαλλόμενων πολύπλοκων συστημάτων που βασίζονται σε μη μαθηματικές έννοιες της αναδρομής, είτε με τη μορφή μιας αναδρομικής διαδικασίας είτε με ένα σύνολο διαφορικών εξισώσεων που μοντελοποιούν ένα φυσικό σύστημα.

ΠΑΡΑΝΟΗΣΕΙΣ ΓΙΑ ΤΗ ΘΕΩΡΙΑ ΤΟΥ ΧΑΟΣ

Το ευρύ κοινό άρχισε να δίνει προσοχή στη θεωρία του χάους χάρη σε ταινίες όπως το Jurassic Park, και χάρη σε αυτές, ο φόβος του κοινού για τη θεωρία του χάους αυξάνεται συνεχώς. Ωστόσο, όπως συμβαίνει με οτιδήποτε καλύπτεται στα μέσα ενημέρωσης, υπάρχουν πολλές παρανοήσεις γύρω από τη θεωρία του χάους.

ΧΑΟΣ ΘΕΩΡΙΑ ΔΙΑΤΑΡΑΧΗΣ

Η πιο κοινή ασυμφωνία είναι ότι οι άνθρωποι πιστεύουν ότι η θεωρία του χάους είναι μια θεωρία για την αταξία. Τίποτα δεν θα μπορούσε να απέχει περισσότερο από την αλήθεια! Αυτό δεν αποτελεί διάψευση του ντετερμινισμού ή ισχυρισμό ότι τα διατεταγμένα συστήματα είναι αδύνατα. αυτό δεν είναι μια άρνηση πειραματικών στοιχείων ή μια δήλωση ότι τα πολύπλοκα συστήματα είναι άχρηστα. Το χάος στη θεωρία του χάους είναι τάξη - και όχι απλώς τάξη, αλλά η ουσία της τάξης.

Είναι αλήθεια ότι η θεωρία του χάους δηλώνει ότι οι μικρές αλλαγές μπορούν να έχουν τεράστιες συνέπειες. Αλλά μια από τις κεντρικές έννοιες στη θεωρία είναι η αδυναμία ακριβούς πρόβλεψης της κατάστασης ενός συστήματος. Γενικά, το έργο της μοντελοποίησης της συνολικής συμπεριφοράς ενός συστήματος είναι αρκετά εφικτό, ακόμη και απλό. Έτσι, η θεωρία του χάους εστιάζει τις προσπάθειές της όχι στην αταξία του συστήματος - την κληρονομική απρόβλεπτη λειτουργία του συστήματος - αλλά στη σειρά που κληρονόμησε - την κοινή συμπεριφορά παρόμοιων συστημάτων.

Επομένως, θα ήταν λάθος να πούμε ότι η θεωρία του χάους αφορά την αταξία. Για να το δείξουμε αυτό με ένα παράδειγμα, ας πάρουμε τον ελκυστήρα Lorentz. Βασίζεται σε τρεις διαφορικές εξισώσεις, τρεις σταθερές και τρεις αρχικές συνθήκες.

Ένας ελκυστής αντιπροσωπεύει τη συμπεριφορά ενός αερίου σε οποιαδήποτε δεδομένη στιγμή και η κατάστασή του σε μια δεδομένη στιγμή εξαρτάται από την κατάστασή του σε χρονικές στιγμές που προηγούνται αυτής της στιγμής. Εάν τα αρχικά δεδομένα αλλάξουν ακόμη και από πολύ μικρές τιμές, ας πούμε, αυτές οι τιμές είναι τόσο μικρές που είναι συγκρίσιμες με τις διακυμάνσεις του αριθμού του Avogadro (πολύ μικρός αριθμός της τάξης των 10 24), ελέγχοντας την κατάσταση του ελκυστήρα θα δείξει εντελώς διαφορετικούς αριθμούς. Αυτό συμβαίνει επειδή οι μικρές διαφορές μεγεθύνονται από την αναδρομή. Ωστόσο, παρόλα αυτά, το γράφημα ελκυστή θα μοιάζει αρκετά. Και τα δύο συστήματα θα έχουν εντελώς διαφορετικές τιμές ανά πάσα στιγμή, αλλά το γράφημα ελκυστήρα θα παραμείνει το ίδιο γιατί εκφράζει τη γενική συμπεριφορά του συστήματος.

Η θεωρία του χάους λέει ότι τα πολύπλοκα μη γραμμικά συστήματα είναι εγγενώς απρόβλεπτα, αλλά την ίδια στιγμή, η θεωρία του χάους λέει ότι ο τρόπος έκφρασης τέτοιων απρόβλεπτων συστημάτων αποδεικνύεται σωστός όχι σε ακριβείς ισότητες, αλλά σε αναπαραστάσεις της συμπεριφοράς του συστήματος - σε περίεργα γραφήματα ελκυστών ή σε φράκταλ. Έτσι, η θεωρία του χάους, την οποία πολλοί άνθρωποι θεωρούν απρόβλεπτη, αποδεικνύεται ταυτόχρονα ότι είναι η επιστήμη της προβλεψιμότητας ακόμη και στα πιο ασταθή συστήματα.

Ωστόσο, σύμφωνα με τα παραπάνω, δεν προκύπτει ότι η θεωρία του χάους δεν έχει εφαρμογές στην πραγματική ζωή.

ΕΦΑΡΜΟΓΗ ΤΗΣ ΘΕΩΡΙΑΣ ΤΟΥ ΧΑΟΣ ΣΤΟΝ ΠΡΑΓΜΑΤΙΚΟ ΚΟΣΜΟ

Όταν εμφανίζονται νέες θεωρίες, όλοι θέλουν να μάθουν τι είναι καλό σε αυτές. Τι καλό λοιπόν έχει η θεωρία του χάους;

Πρώτο και πιο σημαντικό, η θεωρία του χάους είναι μια θεωρία. Αυτό σημαίνει ότι το μεγαλύτερο μέρος της χρησιμοποιείται περισσότερο ως επιστημονική βάση παρά ως άμεσα εφαρμόσιμη γνώση. Η θεωρία του χάους είναι ένας πολύ καλός τρόπος για να δούμε τα γεγονότα που συμβαίνουν στον κόσμο διαφορετικά από την πιο παραδοσιακή σαφώς ντετερμινιστική άποψη που κυριάρχησε στην επιστήμη από τον Νεύτωνα. Οι θεατές που έχουν δει το Jurassic Park αναμφίβολα φοβούνται ότι η θεωρία του χάους μπορεί να επηρεάσει σε μεγάλο βαθμό την ανθρώπινη αντίληψη για τον κόσμο και, στην πραγματικότητα, η θεωρία του χάους είναι χρήσιμη ως μέσο ερμηνείας των επιστημονικών δεδομένων με νέους τρόπους. Αντί για τις παραδοσιακές γραφές X-Y, οι επιστήμονες μπορούν τώρα να ερμηνεύσουν διαγράμματα χώρου φάσης που - αντί να περιγράφουν την ακριβή θέση οποιασδήποτε μεταβλητής σε μια συγκεκριμένη χρονική στιγμή - αντιπροσωπεύουν τη συνολική συμπεριφορά ενός συστήματος. Αντί να εξετάζουμε ακριβείς ισότητες με βάση στατιστικά δεδομένα, μπορούμε τώρα να δούμε δυναμικά συστήματα με συμπεριφορά παρόμοια στη φύση με στατικά δεδομένα - δηλ. συστήματα με παρόμοιους ελκυστήρες. Η θεωρία του χάους παρέχει ένα ισχυρό πλαίσιο για την ανάπτυξη της επιστημονικής γνώσης.

Οι τεχνικές της θεωρίας του χάους έχουν χρησιμοποιηθεί για τη μοντελοποίηση βιολογικών συστημάτων, τα οποία είναι αναμφίβολα μερικά από τα πιο χαοτικά συστήματα που μπορεί κανείς να φανταστεί. Τα συστήματα δυναμικών εξισώσεων έχουν χρησιμοποιηθεί για τη μοντελοποίηση των πάντων, από την αύξηση του πληθυσμού και τις επιδημίες έως τους άρρυθμους καρδιακούς παλμούς.

Στην πραγματικότητα, σχεδόν οποιοδήποτε χαοτικό σύστημα μπορεί να μοντελοποιηθεί - το χρηματιστήριο παράγει καμπύλες που μπορούν εύκολα να αναλυθούν χρησιμοποιώντας περίεργους ελκυστήρες σε αντίθεση με τις ακριβείς σχέσεις. η διαδικασία των σταγονιδίων που πέφτουν από μια βρύση με διαρροή εμφανίζεται τυχαία όταν αναλύεται με γυμνό αυτί, αλλά όταν απεικονίζεται ως ένας παράξενος ελκυστής, αποκαλύπτει μια παράξενη τάξη που δεν θα περίμενε κανείς από τα παραδοσιακά μέσα.

Και, φυσικά, η θεωρία του χάους δίνει στους ανθρώπους έναν εκπληκτικά ενδιαφέροντα τρόπο να αποκτήσουν ενδιαφέρον για τα μαθηματικά, έναν από τους λιγότερο δημοφιλείς τομείς γνώσης σήμερα.

ΤΟ ΚΙΝΗΜΑ BROWNIAN ΚΑΙ ΟΙ ΕΦΑΡΜΟΓΕΣ ΤΟΥ

Η κίνηση Brown είναι, για παράδειγμα, η τυχαία και χαοτική κίνηση των σωματιδίων σκόνης που αιωρούνται στο νερό. Αυτός ο τύπος κίνησης είναι ίσως η πτυχή της γεωμετρίας φράκταλ που έχει την πιο πρακτική χρήση. Η τυχαία κίνηση Brown παράγει ένα μοτίβο συχνότητας που μπορεί να χρησιμοποιηθεί για την πρόβλεψη πραγμάτων που περιλαμβάνουν μεγάλες ποσότητες δεδομένων και στατιστικών. Ένα καλό παράδειγμα είναι η τιμή του μαλλιού, την οποία ο Mandelbrot προέβλεψε χρησιμοποιώντας την κίνηση Brown.

Τα διαγράμματα συχνότητας που δημιουργούνται με γραφική παράσταση αριθμών Brown μπορούν επίσης να μετατραπούν σε μουσική. Φυσικά αυτό το είδος μουσικής φράκταλ δεν είναι καθόλου μουσικό και μπορεί πραγματικά να βαρεθεί τον ακροατή. Σχεδιάζοντας τυχαία αριθμούς Brownian σε ένα γράφημα, μπορείτε να πάρετε ένα Fractal σκόνης όπως αυτό που φαίνεται εδώ ως παράδειγμα.

Εκτός από τη χρήση της κίνησης Brown για την παραγωγή φράκταλ από φράκταλ, μπορεί επίσης να χρησιμοποιηθεί για τη δημιουργία τοπίων. Πολλές ταινίες επιστημονικής φαντασίας, όπως το Star Trek, έχουν χρησιμοποιήσει την τεχνική της κίνησης Brown για να δημιουργήσουν εξωγήινα τοπία όπως λόφους και τοπολογικά μοτίβα ψηλών οροπέδων. Αυτές οι τεχνικές είναι πολύ αποτελεσματικές και μπορούν να βρεθούν στο βιβλίο του Mandelbrot The Fractal Geometry of Nature. Ο Mandelbrot χρησιμοποίησε τις γραμμές Brown για να δημιουργήσει φράκταλ ακτογραμμές και χάρτες νησιών (που στην πραγματικότητα ήταν απλώς τυχαία ζωγραφισμένες κουκκίδες) από την οπτική γωνία του πουλιού.

ΚΙΝΗΣΗ ΜΠΑΛΙΑΣ ΜΠΙΛΙΑΡΔΟΥ

Όποιος έχει πάρει ποτέ ένα σύνθημα πισίνας ξέρει ότι το κλειδί για το παιχνίδι είναι η ακρίβεια. Το παραμικρό σφάλμα στην αρχική γωνία πρόσκρουσης μπορεί γρήγορα να οδηγήσει σε τεράστιο σφάλμα στη θέση της μπάλας μετά από λίγες μόνο κρούσεις. Αυτή η ευαισθησία στις αρχικές συνθήκες, που ονομάζεται χάος, θέτει ένα ανυπέρβλητο εμπόδιο για όποιον ελπίζει να προβλέψει ή να ελέγξει την τροχιά της μπάλας μετά από περισσότερες από έξι ή επτά συγκρούσεις. Και μην νομίζετε ότι το πρόβλημα είναι η σκόνη στο τραπέζι ή ένα ασταθές χέρι. Στην πραγματικότητα, εάν χρησιμοποιείτε τον υπολογιστή σας για να φτιάξετε ένα μοντέλο που περιέχει ένα τραπέζι μπιλιάρδου χωρίς τριβές, χωρίς απάνθρωπο έλεγχο της ακρίβειας τοποθέτησης υπόδειξης, και πάλι δεν θα μπορείτε να προβλέψετε την τροχιά της μπάλας για αρκετό καιρό!

Πόσο καιρό? Αυτό εξαρτάται εν μέρει από την ακρίβεια του υπολογιστή σας, αλλά περισσότερο από το σχήμα του τραπεζιού. Για ένα τέλεια στρογγυλό τραπέζι, μπορούν να υπολογιστούν έως και περίπου 500 θέσεις σύγκρουσης με σφάλμα περίπου 0,1 τοις εκατό. Αλλά αν αλλάξετε το σχήμα του τραπεζιού έτσι ώστε να γίνει τουλάχιστον λίγο ακανόνιστο (οβάλ), και το απρόβλεπτο της τροχιάς μπορεί να ξεπεράσει τις 90 μοίρες μετά από μόλις 10 συγκρούσεις! Ο μόνος τρόπος για να έχετε μια εικόνα της γενικής συμπεριφοράς μιας μπάλας του μπιλιάρδου που αναπηδά από ένα καθαρό τραπέζι είναι να απεικονίσετε τη γωνία αναπήδησης ή το μήκος του τόξου που αντιστοιχεί σε κάθε βολή. Ακολουθούν δύο διαδοχικές μεγεθύνσεις μιας τέτοιας φάσης-χωρικής εικόνας.

Κάθε μεμονωμένος βρόχος ή περιοχή διασποράς αντιπροσωπεύει τη συμπεριφορά της μπάλας που προκύπτει από ένα σύνολο αρχικών συνθηκών. Η περιοχή της εικόνας που εμφανίζει τα αποτελέσματα ενός συγκεκριμένου πειράματος ονομάζεται περιοχή ελκυστήρα για ένα δεδομένο σύνολο αρχικών συνθηκών. Όπως φαίνεται, το σχήμα του πίνακα που χρησιμοποιείται για αυτά τα πειράματα είναι το κύριο μέρος των περιοχών ελκυστήρα, οι οποίες επαναλαμβάνονται διαδοχικά σε φθίνουσα κλίμακα. Θεωρητικά, μια τέτοια αυτο-ομοιότητα θα πρέπει να συνεχιστεί για πάντα και αν μεγεθύνουμε το σχέδιο όλο και περισσότερο, θα παίρναμε όλα τα ίδια σχήματα. Αυτή ονομάζεται μια πολύ δημοφιλής λέξη σήμερα, φράκταλ.

ΕΝΣΩΜΑΤΩΣΗ ΝΤΕΤΕΜΙΝΙΣΤΙΚΩΝ ΦΡΑΚΤΑΛ ΚΑΙ ΧΑΟΣ

Από τα παραδείγματα των ντετερμινιστικών φράκταλ που συζητήθηκαν παραπάνω, μπορούμε να δούμε ότι δεν παρουσιάζουν καμία χαοτική συμπεριφορά και ότι είναι στην πραγματικότητα πολύ προβλέψιμα. Όπως γνωρίζετε, η θεωρία του χάους χρησιμοποιεί ένα φράκταλ για να αναδημιουργήσει ή να βρει μοτίβα προκειμένου να προβλέψει τη συμπεριφορά πολλών συστημάτων στη φύση, όπως, για παράδειγμα, το πρόβλημα της μετανάστευσης των πτηνών.

Τώρα ας δούμε πώς συμβαίνει αυτό στην πραγματικότητα. Χρησιμοποιώντας ένα φράκταλ που ονομάζεται Pythagorean Tree, που δεν συζητήθηκε εδώ (το οποίο, παρεμπιπτόντως, δεν επινοήθηκε από τον Πυθαγόρα και δεν έχει καμία σχέση με το Πυθαγόρειο θεώρημα) και την κίνηση Brown (η οποία είναι χαοτική), ας προσπαθήσουμε να κάνουμε μια μίμηση ενός αληθινό δέντρο. Η σειρά των φύλλων και των κλαδιών σε ένα δέντρο είναι αρκετά περίπλοκη και τυχαία και μάλλον δεν είναι κάτι αρκετά απλό που μπορεί να μιμηθεί ένα σύντομο πρόγραμμα 12 γραμμών.

Πρώτα πρέπει να δημιουργήσετε ένα Πυθαγόρειο Δέντρο. Το αποτέλεσμα θυμίζει εκείνες τις παλιές ζωγραφιές του νηπιαγωγείου. Ας κάνουμε λοιπόν τον κορμό πιο χοντρό. Σε αυτό το στάδιο, η κίνηση Brown δεν χρησιμοποιείται. Αντίθετα, κάθε ευθύγραμμο τμήμα έχει γίνει τώρα μια γραμμή συμμετρίας μεταξύ του ορθογωνίου που γίνεται ο κορμός και των διακλαδώσεων έξω.

Αλλά το αποτέλεσμα εξακολουθεί να φαίνεται πολύ επίσημο και τακτοποιημένο. Το δέντρο δεν φαίνεται να είναι ακόμα ζωντανό. Ας προσπαθήσουμε να εφαρμόσουμε κάποιες από τις γνώσεις στον τομέα των ντετερμινιστικών φράκταλ που μόλις αποκτήσαμε.

Τώρα μπορείτε να χρησιμοποιήσετε την κίνηση Brown για να δημιουργήσετε κάποιο τυχαίο χάος που αλλάζει τους αριθμούς στρογγυλοποιώντας τους σε δύο ψηφία. Το πρωτότυπο χρησιμοποιούσε δεκαδικούς αριθμούς 39-bit. Το αποτέλεσμα (αριστερά) δεν μοιάζει με δέντρο. Αντίθετα, μοιάζει με έξυπνο αγκίστρι!

Ίσως η στρογγυλοποίηση σε 2 ψηφία ήταν υπερβολική; Εφαρμόζουμε ξανά την κίνηση Brown, αυτή τη φορά στρογγυλοποιημένη σε 7 ψηφία. Το αποτέλεσμα εξακολουθεί να μοιάζει με αγκίστρι, αλλά αυτή τη φορά σε σχήμα λογαριθμικής σπείρας!

Εφόσον η αριστερή πλευρά (που περιέχει όλους τους περιττούς αριθμούς) δεν παράγει εφέ αγκίστρου, οι τυχαίες ανωμαλίες που παράγονται από την κίνηση Brown εφαρμόζονται δύο φορές σε όλους τους αριθμούς στην αριστερή πλευρά και μόνο μία φορά στους αριθμούς στα δεξιά. Ίσως αυτό να είναι αρκετό για να εξαλείψει ή να μειώσει την επίδραση της λογαριθμικής σπείρας. Έτσι, οι αριθμοί στρογγυλοποιούνται σε 24 ψηφία. Αυτή τη φορά, το αποτέλεσμα είναι μια ωραία εμφάνιση, μηχανογραφημένη χαοτική εξομοίωση ενός πραγματικού δέντρου.

ΕΝΟΤΗΤΑ 5: ΔΕΝΤΡΟ FEIGENBAUM

ΓΕΝΙΚΕΣ ΠΛΗΡΟΦΟΡΙΕΣ

Η θεωρία του χάους έχει άμεση εφαρμογή στο πρόβλημα της μοντελοποίησης της αύξησης του πληθυσμού και συζητείται εδώ χρησιμοποιώντας το παράδειγμα ενός διαγράμματος Feigenbaum που κατασκευάστηκε χρησιμοποιώντας το πρόγραμμα LT Bifurcator.

ΔΙΑΚΟΣΜΗΣΕΙΣ ΣΕ ΠΛΗΘΥΣΜΙΣΤΙΚΑ ΜΟΝΤΕΛΑ

Το θαύμα της γεωμετρίας φράκταλ είναι ότι μπορούν να παραχθούν εξαιρετικά πολύπλοκα σχήματα από τέτοιες απλές διαδικασίες παραγωγής. Μια άλλη έκπληξη προέρχεται από τη μελέτη των δυναμικών συστημάτων: τέτοιες απλές, ντετερμινιστικές εξισώσεις μπορούν να προκαλέσουν τέτοια χαοτική συμπεριφορά που το σύστημα δεν επιστρέφει ποτέ σε σταθερή κατάσταση και δεν εμφανίζεται κανένα πρότυπο. Συχνά τέτοια συστήματα συμπεριφέρονται αρκετά φυσιολογικά μέχρι μια ορισμένη τιμή μιας βασικής παραμέτρου, μετά βιώνουν μια μετάβαση στην οποία υπάρχουν δύο δυνατότητες για περαιτέρω ανάπτυξη, μετά τέσσερις και, τέλος, ένα χαοτικό σύνολο δυνατοτήτων.

Το 1786, ο Thomas Malthus ανέπτυξε ένα μαθηματικό μοντέλο αύξησης του πληθυσμού και αποδείχθηκε ότι αυτό και άλλα μοντέλα παρόμοιου τύπου έχουν την ιδιότητα που περιγράφηκε παραπάνω. Ας υποθέσουμε ότι έχουμε ένα μοντέλο στο οποίο ο ρυθμός αύξησης του πληθυσμού είναι συνάρτηση, ειδικότερα, του μεγέθους του πληθυσμού:

Νέος πληθυσμός = ρυθμός ανάπτυξης * παλαιός πληθυσμός (1 – παλαιός πληθυσμός)

Όπου ο πληθυσμός είναι κανονικοποιημένος έτσι ώστε να παίρνει τιμές από 0 έως 1. Φυσικά, ένα τέτοιο μοντέλο είναι εξαιρετικά απλοποιημένο και δεν μπορεί να περιγράψει με ακρίβεια τη δυναμική της πληθυσμιακής ανάπτυξης. Όταν ο ρυθμός ανάπτυξης είναι μικρότερος από 200%, αυτό το μοντέλο είναι σταθερό, γιατί για οποιαδήποτε αρχική τιμή, μετά από αρκετές γενιές, το μέγεθος του πληθυσμού καθορίζεται σε σταθερό επίπεδο. Αλλά αν ο ρυθμός ανάπτυξης υπερβαίνει το 200%, η καμπύλη που αντιπροσωπεύει γραφικά την εξίσωση χωρίζεται ή διακλαδίζεται σε δύο διακριτές λύσεις, τότε σε τέσσερις και σύντομα γίνεται χαοτική.

ΔΕΝΤΡΟ FEIGENBAUM

Η λογιστική εξίσωση είναι ο τύπος πάνω στον οποίο εργάστηκε κυρίως ο Mitchell Feigenbaum για να δημιουργήσει τη θεωρία του για τα φράκταλ. Αυτός ο τύπος πρέπει να περιγράφει τη δυναμική της πληθυσμιακής ανάπτυξης:

f(x) = (1 – x)rx

Το απλούστερο μοντέλο είναι μια αναλογική αναλογία του αριθμού προς το προηγούμενο έτος. Ας πούμε πέρυσι είχαμε x ζώα. Θα πρέπει να υπάρχουν rx ζώα φέτος. Αλλά αυτό δεν λειτουργεί σε πραγματικές συνθήκες. Καλύτερη αντιστοιχία με την πραγματικότητα θα προκύψει εάν προσθέσουμε έναν παράγοντα ανάλογα με τις δυνατότητες που έχει ο πληθυσμός για περαιτέρω ανάπτυξη και έστω x ο συντελεστής πληρότητας, ο οποίος ποικίλλει από 0 έως 1. Στη συνέχεια προστεθεί ο παράγοντας 1 – x, έτσι ώστε η περιοχή είναι σχεδόν πλήρως γεμάτη, ο πληθυσμός δεν θα αυξηθεί πάνω από το ανώτατο όριο.

Επεκτείνοντας την λογιστική έκφραση, παίρνουμε:

f(x) = τσεκούρι – τσεκούρι 2

Ο τύπος που χρησιμοποιείται στο πρόγραμμα LT Bifurcator για να εξηγήσει την ουσία του φράκταλ Feigenbaum - (1 + r)x – rx 2 δεν διαφέρει πολύ από τον τύπο που δίνεται παραπάνω. Κατ 'αρχήν, για τη μελέτη της θεωρίας, θα μπορούσε κανείς να χρησιμοποιήσει οποιονδήποτε τύπο, για παράδειγμα, τον απλούστερο από τους τύπους αυτού του τύπου - xI – r. Οι μόνες διαφορές είναι οι διαφορές στις συντεταγμένες των παραθύρων στην εικόνα και μια ελαφρώς διαφορετική εμφάνιση της εικόνας.

ΓΙΑΤΙ ΤΟ ΣΥΣΤΗΜΑ ΓΙΝΕΤΑΙ ΑΠΡΟΒΛΕΠΤΟ;

Δεν είναι εύκολο να εξηγηθεί αυτό το φαινόμενο. Για κάθε σημείο της παραμέτρου r (κατά μήκος της τετμημένης), είναι δυνατές οι ακόλουθες επιλογές για τη συνάρτηση x. Μια συνάρτηση μπορεί να έχει:

· περιοδική τροχιά, δηλ. παίρνει περιοδικά μία ή περισσότερες τιμές, όπως συμβαίνει με το φράκταλ που εμφανίζεται εδώ ως απεικόνιση στο τμήμα 0< r < 2.57

· χαοτική τροχιά, δηλ. παίρνει τόσο μεγάλο αριθμό διαφορετικών τιμών κατά τη διάρκεια της επαναληπτικής διαδικασίας που είναι αδύνατο να βρεθεί οποιοδήποτε μοτίβο, όπως θα μπορούσε να γίνει στην πρώτη περίπτωση

· τιμές που δεν περιορίζονται σε απόλυτη τιμή και αυτό συμβαίνει και στις δύο πλευρές του δέντρου. Επομένως, δεν είναι πλέον δυνατή η εμφάνιση σημείων εδώ.

Στην πρώτη περίπτωση, βλέπουμε μια συνάρτηση που λαμβάνει περιοδικά ορισμένες τιμές. Σε αυτή την περίπτωση, το δέντρο έχει ένα ή περισσότερα κλαδιά. Ο αριθμός των τιμών που παίρνει μια συνάρτηση ονομάζεται περίοδος επανάληψης. Μια συνάρτηση μπορεί να έχει περίοδο από το ένα έως το άπειρο.

Όταν η παράμετρος κυμαίνεται από 0 έως 2, η περίοδος της συνάρτησης είναι ίση με ένα. Στην περίπτωση αυτή, η αντίστοιχη τιμή της συνάρτησης ονομάζεται σταθερό σημείο. Αυτό το σταθερό σημείο αποδεικνύεται η λύση της εξίσωσης

x = (1 + r)x – rx 2

1 + r)x – rx 2 – x = 0

Λύσεις σε αυτήν την εξίσωση:

Εμφανίζοντας αυτές τις λύσεις γραφικά, βλέπουμε ότι ένα από τα γραφήματα (για την περίπτωση προσθήκης όρων στον αριθμητή) αντιστοιχεί ακριβώς στο στέλεχος του δέντρου Feigenbaum μέχρι μια παράμετρο ίση με 2. Οι λύσεις της εξίσωσης ονομάζονται σταθερά σημεία. Εφόσον μόνο μία από τις λύσεις συμπίπτει με το δέντρο Feigenbaum και είναι αποτέλεσμα επαναλήψεων, η δεύτερη συνάρτηση δίνει έλξη σταθερών σημείων.

x=(1+r)x - rx 2 ; r=2,1; x0=0,8

1.136	0.8199	1.1291	0.8234
0.8115	1.1299	0.8229	1.1287
1.1327	0.8215	1.1289	0.8235
0.817	1.1294	0.8232	1.1287
1.1309	0.8224	1.288	0.8236

Στο r = 2, το σταθερό σημείο (δηλαδή μια από τις λύσεις της παραπάνω εξίσωσης) παύει να είναι σταθερό σημείο έλξης και γίνεται απωθητικό. Από αυτή τη στιγμή και μετά, η συνάρτηση δεν συγκλίνει ποτέ σε ένα σημείο. Στη συνέχεια, ξεκινά ένας περιοδικός κύκλος για τη συνάρτηση, με τη συνάρτηση αρχικά να ταλαντώνεται μεταξύ δύο σημείων. Αναλύοντας τα αποτελέσματα που λαμβάνονται, μπορεί κανείς να καταλάβει ότι αυτές οι τιμές μπορούν να θεωρηθούν ως λύσεις που λαμβάνονται με επανάληψη της συνάρτησης δύο φορές. Ας δούμε τι συμβαίνει αν γράψουμε x ως την παρακάτω συνάρτηση

x = [(1 + r)x – rx 2 ] 2 + (1+r)x

Το αποτέλεσμα είναι τέσσερις λύσεις, οι δύο πρώτες από τις οποίες είναι λύσεις στην αρχική έκφραση. Είναι προφανές ότι εμφανίζονται και εδώ. Όμως η τρίτη και η τέταρτη έκφραση παρουσιάζουν ενδιαφέρον. Αν αντικαταστήσουμε το 2.1 σε αυτά (την τιμή που χρησιμοποιήθηκε για τη σύνταξη του πίνακα), παίρνουμε 1.128746121 και 0.823648487, αντίστοιχα, δηλ. τις ίδιες τιμές όπως στον πίνακα. Κάτι που, αυστηρά, ήταν αναμενόμενο. Ενδιαφέρον παρουσιάζει και η γραφική αναπαράσταση της συνάρτησης. Στην πραγματικότητα, παίρνουμε την αρχή ενός δέντρου Fegenbaum. Τα αποδεδειγμένα γεγονότα μπορούν να χρησιμοποιηθούν για τον υπολογισμό των σημείων διακλάδωσης. Η τρίτη και η τέταρτη εξίσωση δεν ορίζονται όταν η τιμή της παραμέτρου είναι μικρότερη από 2, δηλ. όπου διακλαδίζεται η γραμμή.

ΠΑΡΑΘΥΡΑ ΣΤΟ ΔΕΝΤΡΟ FEIGENBAUM

Είναι δύσκολο να πούμε γιατί τα παράθυρα εμφανίζονται σε ένα δέντρο Feigenbaum. Είναι πιο εύκολο να απαντήσετε στο ερώτημα πώς εμφανίζονται. Αυτές είναι οι περιοχές για τις οποίες οι επαναληπτικές τροχιές αντιστοιχούν σε μηδενικά. Για παράδειγμα, αν το αποτέλεσμα της πρώτης επανάληψης δώσει την απάντηση 0, έχουμε ένα παράθυρο. Στην πραγματικότητα, αυτό σημαίνει επίλυση της εξίσωσης: 0 2 – r = 0

ΕΛΚΥΣΤΗΣ ΚΑΙ ΦΑΙΓΕΝΜΠΑΟΥΜ ΚΩΝΣΤΑΝΤ

FEIGENBAUM ΕΛΚΥΣΤΗ

Σε αντίθεση με τη σταθερά του Feigenbaum, αυτός ο αριθμός δεν είναι καθολικός. Η τιμή αυτού του ελκυστήρα εξαρτάται από τον τύπο που χρησιμοποιείται. Για τον τύπο που χρησιμοποιείται στο Lt Bifurcator x = (1 + r)x – rxІ, μπορεί κανείς να βρει γραφικά μια τιμή περίπου ίση με 2,56.

Ο αριθμός αντιπροσωπεύει την τιμή της παραμέτρου στην οποία το γράφημα διέρχεται για πρώτη φορά από έναν άπειρο αριθμό διακλαδώσεων. Αυτό σημαίνει ότι ο ελκυστής Feigenbaum είναι ένας χαοτικός ελκυστής, γιατί η συνάρτηση δεν περνά ποτέ από επαναλαμβανόμενη τροχιά.

Για να υπολογίσετε αυτήν την τιμή, μπορείτε να χρησιμοποιήσετε τη σταθερά του Feigenbaum, αλλά από τότε αυτή η σταθερά εμφανίζεται μόνο με πολλά bufferings· εάν χρειάζεστε αποδεκτή ακρίβεια, στην πράξη αυτό είναι δύσκολο να εφαρμοστεί και δεν έχω καταφέρει ακόμα να χρησιμοποιήσω αυτήν τη μέθοδο.

Θα πρέπει επίσης να σημειωθεί ότι για όλα τα παράθυρα στο διάγραμμα Feigenbaum, υπάρχει μια σταθερή τιμή στην οποία η συνάρτηση διχάζεται άπειρες φορές.

FEIGENBAUM ΚΩΝΣΤΑΝΤ

Αν έπρεπε να δώσω μια σύντομη απάντηση, θα έλεγα: Αυτό είναι περίπου 4.669211660910299067185320382047...

Ωστόσο, αυτό δεν θα ικανοποιούσε κανέναν. Αυτός ο αριθμός είναι ίσως το πιο φανταστικό γεγονός αυτού του φράκταλ. Υπάρχουν πολλοί τύποι που καταλήγουν σε αυτό το δέντρο, αλλά ο αριθμός παραμένει ίδιος όλη την ώρα. Έχει γίνει σχεδόν θρύλος ότι ο Mitchell Feigenbaum τηλεφώνησε στη μητέρα του στο σπίτι όταν ανακάλυψε την ευελιξία και είπε ότι θα τον έκανε διάσημο.

Η περίφημη σταθερά εμφανίζεται όταν συγκρίνετε το μήκος ενός κομματιού ξύλου, δηλ. μέρη μεταξύ της γραμμής των διακλαδώσεων (βλ. εικόνα). Το πρώτο μέρος είναι από 0 έως 2. Το μήκος του είναι 2. Το επόμενο μέρος είναι από 2 έως 2.448 και το μήκος του είναι 0.448. Η αναλογία μεταξύ των δύο μηκών είναι 2/0,448 = 4,4642. Γενικά, αυτή είναι αρκετά κοντά στην τιμή της σταθεράς του Feigenbaum, αλλά, σύμφωνα με τη θεωρία, το αποτέλεσμα μπορεί να βελτιωθεί αν πάρουμε το όριο του λόγου n+1 του μήκους του τμήματος στο n καθώς το n τείνει στο άπειρο (φυσικά, αυτή η τάση περιορίζεται από τον ελκυστήρα Feigenbaum).

Διχοτόμηση αρ.	Σημείο διακλάδωσης	Μήκος τμήματος	Αναλογία μήκους

			4.4642
	2.448	0.448	4.7157
	2.543	0.095	4.5238
	2.564	0.021	4.5652
	2.5686	0.0046	4.1818
	2.5697	0.0011

Φυσικά, αυτό το παράδειγμα είναι απλώς ένα παράδειγμα και δεν διεκδικεί καμία ακρίβεια, γιατί Τα δεδομένα ελήφθησαν αρκετά γρήγορα χρησιμοποιώντας μια καθαρά γραφική μέθοδο.

Είναι σημαντικό να θυμάστε ότι με κάθε διακλάδωση, πρέπει να υπολογίζονται όλο και περισσότερες τιμές για να έχετε ένα ακριβές αποτέλεσμα, επειδή η συνάρτηση απαιτεί περισσότερες επαναλήψεις για να σταθεροποιηθεί. Εάν προσπαθήσετε να κατασκευάσετε ένα δέντρο Feigenbaum από λίγα μόνο σημεία, οι διακλαδώσεις θα συμβούν νωρίτερα από ό,τι στην πραγματικότητα. Αυτό γίνεται όλο και πιο σημαντικό καθώς το δέντρο πλησιάζει όλο και περισσότερο. Χρησιμοποίησα περίπου 1000 επαναλήψεις για τις τιμές που δίνονται στον πίνακα.

ΤΥΧΑΙΑ ΓΕΝΙΑ ΑΡΙΘΜΩΝ

Κοιτάξτε την κατανομή των σημείων κάπου στη δεξιά άκρη του δέντρου Feigenbaum (Ιδιότητες -> Διάστημα -> Γραμμή PseudoChaos στο Lt Bifurcator) Δείτε, φαίνονται πολύ τυχαία. Φαίνεται λοιπόν αρκετά λογικό να χρησιμοποιηθεί αυτό για τη δημιουργία τυχαίων αριθμών.

Το μόνο που έχετε να κάνετε είναι να εκτελέσετε τον τύπο x = (1 + r)x – rx 2 ή κάτι παρόμοιο και να χρησιμοποιήσετε την τελευταία υπολογισμένη τιμή κάθε φορά που χρειάζεται ένας τυχαίος αριθμός. Ναι, αυτό θα λειτουργήσει: θα έχετε μια τροχιά που δεν επαναλαμβάνεται ποτέ γιατί είναι χάος, αλλά δυστυχώς, έλεγξα την κατανομή των πόντων και το αποτέλεσμα δεν ήταν ομοιόμορφο, δηλ. ίσως όχι ίσο για όλα τα διαστήματα.

Οι αριθμοί που υπολογίζονται από τον τύπο βρίσκονται πάντα μεταξύ –2 και 2. Είναι εύκολο να το τεντώσετε στο διάστημα από το 0 έως το 9 και να κάνετε τους αριθμούς ακέραιους. Το έκανα αυτό και μέτρησα πόσες επιτυχίες πήρα για κάθε αριθμό σε πολλές χιλιάδες επαναλήψεις. Ιδού το αποτέλεσμα:

r=1,99999, 50000 επαναλήψεις

10276	3281	3668
4474	3157	4622
3640	3317	10193

μέσος όρος x: 4.501

τυπική απόκλιση x: 3.430

Είναι εύκολο να δει κανείς ότι αυτό δεν δίνει την επιθυμητή κατανομή. Αλλά ίσως να πάρει τις τιμές πιο κοντά στο 3; Νέα δοκιμή:

r=1,99999999999999, 50000 επαναλήψεις

10162	3127	3722
4575	3202	4412
3800	3395	10204

μέσος όρος x: 4,489

τυπική απόκλιση x: 3,425

Δυστυχώς, αυτό μας δίνει σχεδόν την ίδια καμπύλη κατανομής.

Σημείωση

Για να δώσουμε κάποια ιδέα για τον μέσο όρο και την τυπική απόκλιση: Αν είχαμε το αποτέλεσμα που θέλαμε, η συχνότητα κάθε αριθμού μεταξύ 0 και 9 θα ήταν 5000, ο μέσος όρος θα ήταν 4,5 και η τυπική απόκλιση θα ήταν 2,872.

ΣΕΤ FEIGENBAUM ΔΕΝΤΡΟ ΚΑΙ MANDELBROT

Εάν έχετε δει ποτέ τον τύπο πολλαπλότητας Mandelbrot z=z 2 + x, ίσως παρατηρήσετε την ομοιότητα μεταξύ αυτού του τύπου και του απλούστερου από τους τύπους για την κατασκευή του δέντρου Feigenbaum x 2 – r. Και πράγματι είναι. Υπάρχουν ομοιότητες. Αλλά το δέντρο του Feigenbaum μεγαλώνει προς την άλλη κατεύθυνση. Αλλάξτε τον τύπο του Feigenbaum σε x 2 + r και θα δείτε την ομοιότητα. Για το σύνολο Mandelbrot, πρέπει να κοιτάξετε κατά μήκος του οριζόντιου άξονα, καθώς αυτή είναι η μόνη θέση στην οποία το μιγαδικό μέρος του αριθμού Mandelbrot είναι μηδέν. Θα δείτε ότι το κύριο σώμα του σχήματος Mandelbrot είναι όπου η συνάρτηση στο δέντρο Feigenbaum παίρνει μόνο μία τιμή. Όταν συμβεί η πρώτη διαίρεση της γραμμής (διακλάδωση), εμφανίζεται ένα νέο σώμα στη φιγούρα Mandelbrot, κ.λπ. Σημειώστε επίσης ότι όταν ανοίγει το κύριο παράθυρο στο δέντρο, εμφανίζεται ένα παιδικό σώμα στη φιγούρα Mandelbrot.

Εισαγωγή

1. Η εμφάνιση και η ιστορία της θεωρίας του χάους

2. Τάξη και αταξία

3. Εφαρμοσμένο χάος

4. Βασικές αρχές του χάους (ελκυστές και φράκταλ)

6. Χάος σε άλλες επιστήμες

7. Συνέπειες του χάους

1. Ξεκινώντας από τις αρχές της δεκαετίας του 1980 - 1990, μια νέα κατεύθυνση που σχετίζεται με τις «επιστήμες της πολυπλοκότητας» εμφανίστηκε στις συζητήσεις των ιστορικών και των μεθοδολόγων. Αυτό είναι το κοινό όνομα για μια νέα διεπιστημονική περιοχή έρευνας, η εστίαση της οποίας είναι στα προβλήματα της μελέτης συστημάτων με μη γραμμική δυναμική, ασταθή συμπεριφορά, αποτελέσματα αυτοοργάνωσης και παρουσία χαοτικών καθεστώτων. Η ενοποιημένη επιστήμη της συμπεριφοράς των πολύπλοκων συστημάτων και της αυτοοργάνωσης στη Γερμανία ονομάζεται συνέργεια (G. Haken), στις γαλλόφωνες χώρες - η θεωρία των διαλυτικών δομών (I. Prigogine), στις ΗΠΑ - η θεωρία του δυναμικού χάους (M. Feigenbaum). Στην εγχώρια βιβλιογραφία, ο πρώτος όρος υιοθετείται κυρίως, ο πιο συνοπτικός και περιεκτικός.

ΘΕΩΡΙΑ ΤΟΥ ΧΑΟΥΣ- ένας κλάδος των μαθηματικών που μελετά τη φαινομενικά τυχαία ή εξαιρετικά σύνθετη συμπεριφορά ντετερμινιστικών δυναμικών συστημάτων. Ένα δυναμικό σύστημα είναι αυτό του οποίου η κατάσταση αλλάζει με την πάροδο του χρόνου σύμφωνα με σταθερούς μαθηματικούς κανόνες. τα τελευταία καθορίζονται συνήθως από εξισώσεις που σχετίζουν τη μελλοντική κατάσταση του συστήματος με την τρέχουσα. Ένα τέτοιο σύστημα είναι ντετερμινιστικό εάν αυτοί οι κανόνες δεν περιλαμβάνουν ρητά ένα στοιχείο τυχαίας.

Ιστορία της θεωρίας του χάους. Τα πρώτα στοιχεία της θεωρίας του χάους εμφανίστηκαν τον 19ο αιώνα, αλλά αυτή η θεωρία έλαβε αληθινή επιστημονική ανάπτυξη στο δεύτερο μισό του 20ου αιώνα, μαζί με το έργο του Edward Lorentz από το Τεχνολογικό Ινστιτούτο της Μασαχουσέτης και του Γαλλοαμερικανού μαθηματικού Benoit B. Mandelbrot. Ο Edward Lorenz εξέτασε κάποτε τις δυσκολίες στην πρόγνωση του καιρού. Πριν από το έργο του Lorenz, υπήρχαν δύο επικρατούσες απόψεις στον κόσμο της επιστήμης σχετικά με τη δυνατότητα ακριβούς πρόβλεψης του καιρού σε άπειρο χρονικό διάστημα.

Η πρώτη προσέγγιση διατυπώθηκε το 1776 από τον Γάλλο μαθηματικό Pierre Simon Laplace. Ο Laplace δήλωσε ότι «...αν φανταστούμε ένα μυαλό που σε μια δεδομένη στιγμή έχει κατανοήσει όλες τις συνδέσεις μεταξύ των αντικειμένων στο Σύμπαν, τότε θα είναι σε θέση να καθορίσει την αντίστοιχη θέση, τις κινήσεις και τα γενικά αποτελέσματα όλων αυτών των αντικειμένων ανά πάσα στιγμή στο παρελθόν ή στο μέλλον». Αυτή η προσέγγισή του έμοιαζε πολύ με τα περίφημα λόγια του Αρχιμήδη: «Δώσε μου ένα υπομόχλιο και θα γυρίσω όλο τον κόσμο ανάποδα».

Έτσι, ο Laplace και οι υποστηρικτές του είπαν ότι για να προβλέψουμε με ακρίβεια τον καιρό, είναι απαραίτητο μόνο να συλλέξουμε περισσότερες πληροφορίες για όλα τα σωματίδια στο Σύμπαν, τη θέση τους, την ταχύτητα, τη μάζα, την κατεύθυνση κίνησης, την επιτάχυνση κ.λπ. Ο Laplace σκέφτηκε ότι όσο περισσότερα γνωρίζει ένας άνθρωπος, τόσο πιο ακριβής θα είναι η πρόβλεψή του για το μέλλον.

Η δεύτερη προσέγγιση για τη δυνατότητα πρόβλεψης καιρού διατυπώθηκε με μεγαλύτερη σαφήνεια πριν από οποιονδήποτε άλλον από έναν άλλο Γάλλο μαθηματικό, τον Ζυλ Ανρί Πουανκαρέ. Το 1903 είπε: " Αν γνωρίζαμε ακριβώς τους νόμους της φύσης και τη θέση του Σύμπαντος την αρχική στιγμή, θα μπορούσαμε να προβλέψουμε με ακρίβεια τη θέση του ίδιου Σύμπαντος σε μια επόμενη στιγμή. Αλλά ακόμα κι αν οι νόμοι της φύσης μας αποκάλυπταν όλα τα μυστικά τους, ακόμα και τότε θα μπορούσαμε να γνωρίζουμε την αρχική θέση μόνο κατά προσέγγιση.

Αν αυτό μας επέτρεπε να προβλέψουμε την επακόλουθη κατάσταση με την ίδια προσέγγιση, αυτό θα ήταν το μόνο που ζητούσαμε, και θα μπορούσαμε να πούμε ότι το φαινόμενο είχε προβλεφθεί, ότι διέπεται από νόμους. Αλλά δεν συμβαίνει πάντα. μπορεί να συμβεί μικρές διαφορές στις αρχικές συνθήκες να προκαλούν πολύ μεγάλες διαφορές στο τελικό φαινόμενο. Ένα μικρό λάθος στο πρώτο θα δημιουργήσει ένα τεράστιο λάθος στο δεύτερο.

Η πρόβλεψη γίνεται αδύνατη και έχουμε να κάνουμε με ένα φαινόμενο που εξελίσσεται τυχαία». .

Σε αυτά τα λόγια του Πουανκαρέ βρίσκουμε το αξίωμα της θεωρίας του χάους για την εξάρτηση από τις αρχικές συνθήκες. Η μετέπειτα ανάπτυξη της επιστήμης, ιδιαίτερα της κβαντικής μηχανικής, διέψευσε τον ντετερμινισμό του Laplace. Το 1927, ο Γερμανός φυσικός Βέρνερ Χάιζενμπεργκ ανακάλυψε και διατύπωσε την αρχή της αβεβαιότητας. Αυτή η αρχή εξηγεί γιατί ορισμένα τυχαία φαινόμενα δεν υπακούουν στον Λαπλασιανό ντετερμινισμό.

Ο Heisenberg έδειξε την αρχή της αβεβαιότητας χρησιμοποιώντας το παράδειγμα της ραδιενεργού πυρηνικής διάσπασης. Έτσι, λόγω του πολύ μικρού μεγέθους του πυρήνα, είναι αδύνατο να γνωρίζουμε όλες τις διεργασίες που συμβαίνουν μέσα σε αυτόν. Επομένως, ανεξάρτητα από το πόσες πληροφορίες συλλέγουμε για τον πυρήνα, είναι αδύνατο να προβλεφθεί με ακρίβεια πότε αυτός ο πυρήνας θα αποσυντεθεί.

Το 1926–1927, ο Ολλανδός μηχανικός B. Van der Pol σχεδίασε ένα ηλεκτρονικό κύκλωμα που αντιστοιχεί σε ένα μαθηματικό μοντέλο καρδιακών συσπάσεων. Ανακάλυψε ότι, υπό ορισμένες συνθήκες, οι ταλαντώσεις που συνέβαιναν στο κύκλωμα δεν ήταν περιοδικές, όπως σε έναν κανονικό καρδιακό παλμό, αλλά ακανόνιστες. Το έργο του έλαβε σοβαρή μαθηματική τεκμηρίωση κατά τη διάρκεια του Β' Παγκοσμίου Πολέμου, όταν ο J. Littlewood και ο M. Cartwright εξερεύνησαν τις αρχές του ραντάρ.

Το 1950, ο J. von Neumann πρότεινε ότι η αστάθεια του καιρού θα μπορούσε μια μέρα να αποδειχθεί καλό, καθώς η αστάθεια σήμαινε ότι το επιθυμητό αποτέλεσμα θα μπορούσε να είναι

Στις αρχές της δεκαετίας του 1960, ο Αμερικανός μαθηματικός S. Smale προσπάθησε να κατασκευάσει μια εξαντλητική ταξινόμηση των τυπικών τύπων συμπεριφοράς των δυναμικών συστημάτων. Στην αρχή υπέθεσε ότι μπορούσε να αρκεστεί σε διάφορους συνδυασμούς περιοδικών κινήσεων, αλλά σύντομα συνειδητοποίησε ότι ήταν δυνατή η πολύ πιο περίπλοκη συμπεριφορά. Ειδικότερα, μελέτησε λεπτομερέστερα τη σύνθετη κίνηση που ανακάλυψε ο Πουανκαρέ στο πρόβλημα των περιορισμένων τριών σωμάτων, απλοποιώντας τη γεωμετρία και αποκτώντας ένα σύστημα γνωστό πλέον ως «Μικρό πέταλο». Απέδειξε ότι ένα τέτοιο σύστημα, παρά τον ντετερμινισμό του, παρουσιάζει κάποια χαρακτηριστικά τυχαίας συμπεριφοράς. Άλλα παραδείγματα παρόμοιων φαινομένων αναπτύχθηκαν από την αμερικανική και τη ρωσική σχολή στη θεωρία των δυναμικών συστημάτων, με τη συμβολή του V.I. Arnold να είναι ιδιαίτερα σημαντική. Έτσι άρχισε να αναδύεται η γενική θεωρία του χάους.

Το γεγονός ότι η ευαισθησία στα αρχικά δεδομένα οδηγεί σε χάος έγινε αντιληπτό -και το 1963- από Αμερικανό μετεωρολόγο Έντουαρντ Λόρεντς. Αναρωτήθηκε: γιατί η ραγδαία βελτίωση των υπολογιστών δεν οδήγησε στην πραγματοποίηση του ονείρου των μετεωρολόγων - μια αξιόπιστη μεσοπρόθεσμη (2-3 εβδομάδες νωρίτερα) πρόγνωση καιρού; Ο Edward Lorenz πρότεινε ένα απλό μοντέλο που περιγράφει τη μεταφορά αέρα (παίζει σημαντικό ρόλο στη δυναμική της ατμόσφαιρας), το υπολόγισε σε έναν υπολογιστή και δεν φοβήθηκε να πάρει το αποτέλεσμα στα σοβαρά. Αυτό το αποτέλεσμα - το δυναμικό χάος - είναι μια μη περιοδική κίνηση σε ντετερμινιστικά συστήματα (δηλαδή σε εκείνα όπου το μέλλον καθορίζεται μοναδικά από το παρελθόν), που έχει πεπερασμένο ορίζοντα πρόβλεψης.

Από μαθηματική άποψη, μπορούμε να υποθέσουμε ότι οποιοδήποτε δυναμικό σύστημα, ανεξάρτητα από το τι μοντελοποιεί, περιγράφει την κίνηση ενός σημείου στο χώρο, που ονομάζεται χώρος φάσης. Το πιο σημαντικό χαρακτηριστικό αυτού του χώρου είναι η διάστασή του, ή, με απλά λόγια, ο αριθμός των αριθμών που πρέπει να καθοριστούν για να προσδιοριστεί η κατάσταση του συστήματος. Από μαθηματική και υπολογιστική άποψη, δεν είναι τόσο σημαντικό ποιοι είναι αυτοί οι αριθμοί - ο αριθμός των λύγκων και των λαγών σε μια συγκεκριμένη περιοχή, οι μεταβλητές που περιγράφουν την ηλιακή δραστηριότητα ή το καρδιογράφημα ή το ποσοστό των ψηφοφόρων που εξακολουθούν να υποστηρίζουν τον πρόεδρο. Αν υποθέσουμε ότι ένα σημείο, που κινείται σε χώρο φάσης, αφήνει ένα ίχνος πίσω του, τότε ένα κουβάρι τροχιών θα αντιστοιχεί σε δυναμικό χάος. Εδώ η διάσταση του χώρου φάσης είναι μόνο 3. Είναι αξιοσημείωτο ότι τέτοια εκπληκτικά αντικείμενα υπάρχουν ακόμη και στον τρισδιάστατο χώρο.

2. Τάξη και αταξία

Η θεωρία του χάους είναι αρκετά γενική ώστε να καλύπτει ένα ευρύ φάσμα φαινομένων στον κόσμο μας και ταυτόχρονα εξάπτει τη φαντασία των αναγνωστών. Τελικά, αποδείχθηκε ότι η τάξη προκύπτει ακριβώς από το χάος, και όχι από κάπου αλλού! Από την άλλη πλευρά, στις σύγχρονες επιστημονικές ιδέες για το χάος υπάρχουν πολλά σημεία που απαιτούν ιδιαίτερη προσοχή και σε βάθος μελέτη. Ίσως υπάρχουν περισσότερες ερωτήσεις εδώ παρά απαντήσεις.

Τάξη και αταξία

Για λόγους που ίσως θα γίνουν σαφείς παρακάτω, θα στραφούμε πρώτα σε δύο εξαιρετικά σημαντικές έννοιες της σύγχρονης επιστήμης: «τάξη» και «αταξία». Συνήθως μας φαίνεται ότι όλα εδώ είναι ξεκάθαρα και κατανοητά από την αρχή, αλλά στην πραγματικότητα αυτό απέχει πολύ από την περίπτωση. Και η έννοια του χάους, ως ένα βαθμό, γίνεται ενδιαφέρουσα και σημαντική ακριβώς γιατί δεν μπορούμε να τα καταφέρουμε εδώ μόνο με τάξη και αταξία.

Καταρχήν τι είναι τάξη και τι αταξία; Ποια είναι η σχέση τους μεταξύ τους; Και πώς να ξεχωρίσετε το ένα από το άλλο; Αυτά τα ερωτήματα, όπως αποδεικνύεται, δεν είναι καθόλου ασήμαντα, όπως θα δούμε σύντομα.

Στην καθημερινή ζωή, είναι σύνηθες να πιστεύουμε ότι η διαταραχή είναι έλλειψη τάξης. Τέτοιες έννοιες εμφανίζονται αρκετά συχνά, για παράδειγμα "κρύο". Το χρησιμοποιούμε σε κάθε βήμα και καταλαβαίνουμε τι σημαίνει. Επιπλέον, το «μετράμε» ακόμη και με ένα θερμόμετρο. Κι όμως, κρύο ως τέτοιο δεν υπάρχει. Υπάρχει ζέστη, και το κρύο είναι στην πραγματικότητα το μειονέκτημά του. Αλλά λέμε «κρύο» σαν να ήταν κάτι πραγματικό (ή, όπως λένε οι φιλόσοφοι, ουσιαστικό).

Αλλά με την έννοια της «διαταραχής» τα πάντα, υπό μια ορισμένη έννοια, είναι το αντίθετο. Χρησιμοποιούμε αυτή τη λέξη για να δηλώσουμε την απουσία κάτι (τάξης), το οποίο ακριβώς υπάρχει από μόνο του. Όμως τίθεται το ερώτημα: είναι έτσι;

Ας εξηγήσουμε την ουσία του θέματος με ένα συγκεκριμένο παράδειγμα, για το οποίο φανταζόμαστε το γραφείο ενός συγκεκριμένου καθηγητή. Κοιτάζοντάς το, πιθανότατα θα αποφασίσουμε ότι ό,τι υπάρχει πάνω του έχει πεταχτεί σε έναν άτακτο σωρό. Ωστόσο, ο ίδιος ο καθηγητής, χωρίς να κοιτάξει, απλώνοντας το χέρι του, βρίσκει αναμφισβήτητα το αντικείμενο που χρειάζεται. Και αντίθετα, αν η καθαρίστρια τακτοποιήσει τα πάντα σε τακτοποιημένα στοίβες, τότε ο καθηγητής δεν θα μπορεί να εργαστεί με τον ίδιο τρόπο που η γιαγιά στο μυθιστόρημα του Ray Bradbury «Dandelion Wine» δεν μπορούσε να μαγειρέψει μετά το γενικό καθάρισμα που κανονίστηκε στην κουζίνα. από τη θεία της.

Ίσως πρέπει να παραδεχτούμε ότι αυτό που έχουμε συνηθίσει να αποκαλούμε αταξία δεν είναι σε καμία περίπτωση η απουσία αυτού που συνήθως αποκαλείται τάξη; Ωστόσο, υπάρχει ένας άλλος τρόπος: να αφήσουμε πίσω τη λέξη «ακαταστασία» τη συνηθισμένη της σημασία και να εισαγάγουμε έναν άλλο όρο για να δηλώσουμε αυτό που συχνά, χωρίς σκέψη, ονομάζουμε επίσης διαταραχή, αν και στην πραγματικότητα εννοούμε κάτι εντελώς διαφορετικό.

Πρόσφατα, η λέξη «χάος» διεκδικεί όλο και περισσότερο το ρόλο μιας τέτοιας έννοιας.

Αυστηρά μιλώντας, θα πρέπει να γίνει διάκριση μεταξύ του απλού «χάους» και του «ντετερμινιστικού χάους». Θα δούμε τι είναι αυτό παρακάτω, αλλά προς το παρόν ας σημειώσουμε δύο σημεία.

Πρώτον, σύμφωνα με τη λογική των πραγμάτων, το ντετερμινιστικό χάος πρέπει να είναι μια ειδική περίπτωση χάους, και με αυτή την έννοια θα πρέπει να εισαχθούν τρεις όροι: η γενική έννοια του χάους και, ως δύο από τις ειδικές περιπτώσεις του, το ντετερμινιστικό και το ακαθόριστο χάος. Τότε το ακαθοριστικό χάος θα μπορούσε να είναι το ισοδύναμο της αταξίας, και το ντετερμινιστικό χάος υποδηλώνει κάτι ποιοτικά διαφορετικό από αυτό (ακριβώς αυτό για το οποίο θα μιλήσουμε).

Δεύτερον, όπως αποδεικνύεται με τη σε βάθος ανάλυση, η διαφορά μεταξύ ντετερμινιστικού και ακαθοριστικού χάους στην πραγματικότητα δεν είναι τόσο θεμελιώδης όσο πιστεύεται συνήθως και είναι περισσότερο μεθοδολογική παρά φυσική. Ως εκ τούτου, στις προτεινόμενες σημειώσεις θα μιλήσουμε απλώς για χάος, διευκρινίζοντας το αντικείμενο συζήτησης εκεί που πραγματικά χρειάζεται. Επιπλέον, η απλή, λακωνική και λακωνική λέξη «χάος» έχει μια ορισμένη αισθητική έλξη, η οποία δεν μπορεί να ειπωθεί για το αυστηρό, αλλά μακρύ και βαρετό «ντετερμινιστικό χάος». Άλλωστε, ο Prigogine είπε «Τάξη από το χάος» και όχι «Τάξη από ντετερμινιστικό χάος».

Στον αρχαίο κόσμο, η λέξη «χάος» σήμαινε την ανοργάνωτη κατάσταση της ύλης στην οποία υπήρχε πριν από το σύμπαν, και με αυτή την έννοια μπορεί κάλλιστα να εκληφθεί ως συνώνυμο της λέξης «διαταραχή». Αλλά, ταυτόχρονα, μια τέτοια κατανόηση περιέχει κάτι που γεννά άλλες έννοιες. Πιθανώς, εάν το επιθυμείτε, το χάος θα μπορούσε να ονομαστεί υπερτάξη, που σημαίνει ότι περιέχει δυνητικά πολλές διαφορετικές τάξεις, καθεμία από τις οποίες, υπό ορισμένες συνθήκες, μπορεί να πραγματοποιηθεί, δημιουργώντας τον δικό της κόσμο.

Ωστόσο, ας επιστρέψουμε στην τάξη και την αταξία ως τέτοια. Αν δούμε την κατάσταση των πραγμάτων με ανοιχτό μυαλό, θα δούμε ότι κατά παραγγελία συχνά δεν σημαίνουν τίποτα περισσότερο από χωρική ή χωροχρονική κανονικότητα, η οποία βασίζεται στη μια ή στην άλλη συμμετρία. Γι' αυτό, κοιτάζοντας το τραπέζι κάποιου άλλου, θέλουμε να δούμε εκεί συμμετρικά διατεταγμένα αντικείμενα (η στάση μας απέναντι στο τραπέζι μας είναι συνήθως κάπως διαφορετική).

Εδώ πρέπει να σημειωθεί ένα εξαιρετικά σημαντικό σημείο. Η συμπεριφορά ενός συστήματος με κανονική δομή, κατά κανόνα, μπορεί να προβλεφθεί (πιθανότατα σε επίπεδο πιθανοτήτων) και ακριβώς με βάση τα στοιχεία συμμετρίας που υπάρχουν σε αυτό. Αν γνωρίζουμε ότι τα μολύβια βρίσκονται στη δεξιά γωνία του τραπεζιού, τότε είναι απίθανο να βρούμε ένα από αυτά στην κοντινή αριστερή γωνία. Η τάξη του κόσμου είναι ακριβώς αυτό που μας επιτρέπει να πλοηγηθούμε σε αυτόν. Από αυτή την άποψη, η κύρια κοινή ιδιότητα τόσο των διαταραγμένων όσο και των χαοτικών καταστάσεων ενός συστήματος είναι ότι δεν μπορούμε να προβλέψουμε τη συμπεριφορά του. Σε αυτή την περίπτωση, η συμπεριφορά μπορεί να έχει τόσο χρονική όσο και χωρική ερμηνεία. Στην πρώτη περίπτωση, εννοούμε την αδυναμία να πούμε σε ποια κατάσταση θα βρίσκεται το σύστημα σε μια δεδομένη χρονική στιγμή, και στη δεύτερη, ποια θα είναι η χωρική του διαμόρφωση.

Ίσως είναι η εσωτερική (και όχι πάντα συνειδητή) επιθυμία μας να ζήσουμε σε έναν προβλέψιμο κόσμο που κάνει τα τακτοποιημένα συστήματα ελκυστικά. Και το γεγονός ότι το χάος, προφανώς, ως προς τις πιθανές δυνατότητες, είναι ασύγκριτα πλουσιότερο από την τάξη, δεν αλλάζει την κατάσταση. Θέλουμε ή άθελά μας, το αντιλαμβανόμαστε ως κάτι τρομακτικό και ξένο στην καθημερινή μας συνείδηση.

Σε πνευματικό επίπεδο, μας είναι λίγο-πολύ ξεκάθαρο ότι η τάξη ενός συστήματος, ό,τι κι αν είναι στην πραγματικότητα, σχετίζεται κατά κάποιο τρόπο με την πολυπλοκότητά του. Είναι πιο δύσκολο να χτίσεις ένα σπίτι παρά να το καταστρέψεις. Η δημιουργία προϋποθέτει την τάξη, ενώ η καταστροφή προϋποθέτει αταξία. Ένα χτισμένο σπίτι έχει στοιχεία που έχουν συγκεκριμένους λειτουργικούς ρόλους, αλλά ένας σωρός από μπάζα όχι.

Είναι όμως πάντα προφανής η πολυπλοκότητα και καθορίζεται πάντα από τη συμμετρία; Ας θυμηθούμε ξανά το γραφείο του καθηγητή: η διάταξη των αντικειμένων πάνω του είναι εντελώς ακανόνιστη, αλλά αρκετά περίπλοκη. Εάν δεν με πιστεύετε, προσπαθήστε να εξηγήσετε πώς ο καθηγητής βρίσκει το απαιτούμενο αντικείμενο.

Επομένως, θα πρέπει να αναγνωριστεί ότι υπάρχουν συστήματα που έχουν υψηλό επίπεδο πολυπλοκότητας, αλλά ταυτόχρονα στερούνται εμφανούς κανονικότητας. Μας φαίνεται ότι δεν υπάρχουν συνδέσεις μεταξύ των στοιχείων τους και ότι βρίσκονται τυχαία, ενώ στην πραγματικότητα οι συνδέσεις υπάρχουν, αλλά είναι πολύ περίπλοκες για να τις δούμε. Επομένως, δεν θα είναι λάθος να πούμε ότι η τάξη με τη συνήθη έννοια είναι κάτι μεταξύ αταξίας και χάους. Εάν είναι επιθυμητό, η τάξη μπορεί να οριστεί ως χάος με μια έκδηλη δομή και η αταξία ως η απουσία δομής (μόλις αρχίσουμε να βλέπουμε συνδέσεις μεταξύ των στοιχείων του συστήματος, γίνεται τάξη για εμάς). Γι' αυτό το χάος είναι έννοια ανεξάρτητη και αυτάρκης, γιατί η μη εκδήλωση κάτι δεν σημαίνει και την απουσία του.

Η αταξία και το χάος σε ένα σύστημα είναι παρόμοια μεταξύ τους καθώς δεν βλέπουμε μοτίβα στη διάταξη των στοιχείων του. Η διαφορά έγκειται στο γεγονός ότι στην περίπτωση της αταξίας πραγματικά δεν υπάρχουν, και στην περίπτωση του χάους υπάρχουν, αλλά όχι στην πραγματική διάταξη των στοιχείων την τρέχουσα χρονική στιγμή, αλλά σε εκείνους τους εσωτερικούς μηχανισμούς που δημιουργούν αυτό συμφωνία. Επιπλέον (και αυτό είναι το πιο αξιοσημείωτο), τέτοιοι μηχανισμοί μπορούν να εφαρμοστούν φυσικά έξω από το σύστημα, για παράδειγμα, στο μυαλό ενός καθηγητή που ξέρει πού βρίσκονται τα πάντα στο γραφείο του. Γι' αυτό τα αντικείμενα στο τραπέζι φαίνονται να βρίσκονται τυχαία σε όλους εκτός από τον ίδιο τον καθηγητή, αφού μόνο αυτός γνωρίζει την αρχή της τοποθέτησής τους.

3. Εφαρμοσμένο χάος

Συχνά συζητείται το ερώτημα: σε τι χρησιμεύει το χάος;

Καταρχάς, δεν μπορεί κανείς να υποτιμήσει την κολοσσιαία ιδεολογική σημασία αυτής της έννοιας. Ο κόσμος γύρω μας είναι γεμάτος από μη γραμμικά φαινόμενα και διαδικασίες, η σωστή κατανόηση των οποίων είναι αδιανόητη χωρίς να κατανοήσουμε την πιθανότητα χάους, καθώς και τους σχετικούς θεμελιώδεις περιορισμούς στην προβλεψιμότητα της συμπεριφοράς πολύπλοκων συστημάτων. Για παράδειγμα, η ασυνέπεια του δόγματος της μοναδικής βεβαιότητας της ιστορικής διαδικασίας γίνεται αρκετά εμφανής.

Αυτό δεν μας εμποδίζει να συζητήσουμε τη δυνατότητα χρήσης του χάους σε συστήματα διαφόρων φύσεων για συγκεκριμένους πρακτικούς σκοπούς ή να λάβουμε υπόψη τις συνέπειες που μπορεί να οδηγήσει η εμφάνιση πολύπλοκων δυναμικών.

Ας δώσουμε ένα απλό παράδειγμα - το πρόβλημα της δυναμικής ενός πλοίου ή μιας πλατφόρμας πετρελαίου παρουσία κυμάτων. Σε μια ορισμένη προσέγγιση, αυτό είναι ένα μη γραμμικό δυναμικό σύστημα με εξωτερική περιοδική επίδραση. Η κανονική θέση εργασίας του σκάφους αντιστοιχεί σε έναν ελκυστήρα του συστήματος, ενώ η ανεστραμμένη θέση αντιστοιχεί σε έναν άλλο. Μπορεί κανείς να αναρωτηθεί πώς βρίσκεται η πισίνα έλξης του δεύτερου ελκυστήρα και πώς είναι δομημένη. Πώς εξαρτάται από την ένταση του ενθουσιασμού; Είναι ξεκάθαρο ότι το να μπεις στη δεξαμενή έλξης του δεύτερου ελκυστήρα οδηγεί σε καταστροφή! Τονίζουμε ότι μόνο η μη γραμμική ανάλυση παρέχει ολοκληρωμένη κατανόηση της κατάστασης, ανάπτυξη συνθηκών και συστάσεις για την αποφυγή μιας καταστροφής.

Λόγω της δυναμικής φύσης των χαοτικών καθεστώτων και της ευαισθησίας τους σε μικρές διαταραχές, επιτρέπουν αποτελεσματικό έλεγχο μέσω εξωτερικών ελεγχόμενων επιρροών. Ο σκοπός μιας τέτοιας επιρροής μπορεί να είναι η εφαρμογή ενός περιοδικού καθεστώτος στο σύστημα αντί του χάους ή η είσοδος σε μια δεδομένη περιοχή του χώρου φάσης. Αυτή η ιδέα, που προτάθηκε αρχικά από μια ομάδα Αμερικανών ερευνητών από το Πανεπιστήμιο του Μέριλαντ, φαίνεται πολλά υποσχόμενη και γόνιμη από άποψη εφαρμογής. Μέχρι σήμερα, υπάρχει εκτενής βιβλιογραφία για το θέμα αυτό, ενώ έχουν πραγματοποιηθεί πολλά διεθνή επιστημονικά συνέδρια.

Επιτυχημένα παραδείγματα ελέγχου χάους εφαρμόζονται σε μηχανικά συστήματα, ηλεκτρονικές συσκευές και λέιζερ. Ένα παράδειγμα είναι μια εργασία που εξετάζει τη χρήση τεχνικών ελέγχου του χάους προκειμένου να κατευθύνει ένα διαστημόπλοιο στη Σελήνη. Αποδεικνύεται ότι με τη βοήθεια μικρών ελεγχόμενων επιρροών το πρόβλημα μπορεί να λυθεί με πολύ σημαντική εξοικονόμηση καυσίμου, αν και με κόστος αύξησης της διάρκειας πτήσης.

Μια άλλη κατεύθυνση εφαρμογής ιδεών και μεθόδων μη γραμμικής δυναμικής σχετίζεται με το πρόβλημα της επεξεργασίας σήματος. Ας φανταστούμε ότι ερευνούμε ένα απομακρυσμένο και απρόσιτο αντικείμενο, έτσι ώστε οι δυνατότητές μας να περιορίζονται στην ανάλυση του σήματος που προέρχεται από αυτό. Τα τελευταία χρόνια, έχουν προταθεί τεχνικές για τον προσδιορισμό του εάν ένα σήμα παράγεται από ένα δυναμικό σύστημα, καθώς και για τη λήψη πληροφοριών σχετικά με τις ιδιότητες και τα χαρακτηριστικά αυτού του συστήματος. Έτσι, η συσκευή της μη γραμμικής δυναμικής μετατρέπεται σε ένα εργαλείο έρευνας που επιτρέπει σε κάποιον να κάνει ένα συμπέρασμα ή υπόθεση για τη δομή ενός αντικειμένου, να κατασκευάσει το δυναμικό του μοντέλο κ.λπ. Η ανάπτυξη μεθόδων και αλγορίθμων για την ανάλυση σήματος μπορεί να θεωρηθεί σημαντικός τομέας μη γραμμικής δυναμικής, που σχετίζεται άμεσα με πιθανές εφαρμογές.

Οι προοπτικές για τη χρήση τεχνικών ανάλυσης και επεξεργασίας σήματος, κατασκευής μοντέλων και τεχνικών ελέγχου του χάους σε σχέση με προβλήματα στην ιατρική και τη βιολογία εκτιμώνται ιδιαίτερα.

Στη ραδιομηχανική και την ηλεκτρονική, είναι γνωστές πολλές εφαρμογές όπου χρειάζονται γεννήτριες ταλαντώσεων που μοιάζουν με θόρυβο, οι οποίες μπορούν να αναπαραχθούν από διάφορες συσκευές που λειτουργούν στη λειτουργία δυναμικού χάους. Παραδείγματα περιλαμβάνουν ταλαντωτές χρονικής καθυστέρησης που χρησιμοποιούν έναν σωλήνα κινούμενου κύματος.

Μία από τις πιθανές εφαρμογές του χάους είναι η χρήση χαοτικών σημάτων που παράγονται από δυναμικά συστήματα για σκοπούς επικοινωνίας. Η χαοτική φύση των σημάτων ανοίγει νέες δυνατότητες για την κωδικοποίηση πληροφοριών που γίνεται δύσκολο να υποκλαπούν. Έχει προταθεί ένας αριθμός σχημάτων που παρέχουν επικοινωνία σε χαοτικά σήματα και έχουν πραγματοποιηθεί πειράματα επίδειξης.

Τα αποτελέσματα που λαμβάνονται στη μη γραμμική δυναμική ανοίγουν νέες μη ασήμαντες δυνατότητες για συμπίεση, αποθήκευση και επεξεργασία πληροφοριών. Ένα ενδιαφέρον παράδειγμα αυτού του είδους μπορεί να είναι το σχέδιο κωδικοποίησης και επεξεργασίας πληροφοριών χρησιμοποιώντας μονοδιάστατες χαρτογραφήσεις που προτείνεται στο Ινστιτούτο Ραδιομηχανικής και Ηλεκτρονικής της Ρωσικής Ακαδημίας Επιστημών. Έχουν αναπτυχθεί αποτελεσματικές μέθοδοι συμπίεσης πληροφοριών με βάση τις ιδέες της γεωμετρίας φράκταλ. Διερευνάται το ζήτημα της εφαρμογής υπολογιστικών διαδικασιών σε συστήματα διαφορετικά από την παραδοσιακή αρχιτεκτονική υπολογιστών και βασισμένα στα φαινόμενα της μη γραμμικής δυναμικής.

4.Βασικές αρχές. Για τη μελέτη του χάους, χρησιμοποιούνται γενικές μαθηματικές αρχές και μοντελοποίηση υπολογιστή. Το θεμελιώδες χαρακτηριστικό κάθε δυναμικού συστήματος είναι η επανάληψη, δηλ. το αποτέλεσμα επαναλαμβανόμενης (πολλαπλής) εφαρμογής του ίδιου μαθηματικού κανόνα σε κάποια επιλεγμένη κατάσταση. Η κατάσταση περιγράφεται συνήθως από έναν αριθμό ή ένα σύνολο αριθμών, αλλά μπορεί επίσης να είναι ένα γεωμετρικό σχήμα ή διαμόρφωση.

Η κύρια έννοια της θεωρίας του χάους είναι οι ελκυστές και τα φράκταλ.

Ελκυστήρας

(από τα αγγλικά να προσελκύω - προσελκύω) - μια γεωμετρική δομή που χαρακτηρίζει τη συμπεριφορά στο χώρο φάσης μετά από πολύ καιρό. Εδώ καθίσταται απαραίτητος ο ορισμός της έννοιας του χώρου φάσης.

Τέσσερις ελκυστήρες αποτελούν τη βασική δομή του εξωτερικού κόσμου, τη φύση της συμπεριφοράς και τις κινήσεις της αγοράς. Η θεωρία του χάους βρίσκεται σε πλήρη αντίφαση με την αναλυτική θεωρία. Μας δίνει μια νέα μεταφυσική. Επικεντρώνεται σε αυτό που συμβαίνει αυτή τη στιγμή, το οποίο είναι πολύ πιο σημαντικό κατά την ανάλυση της αγοράς. Η θεωρία του χάους δίνει μια πιο ολοκληρωμένη εικόνα, καλύπτοντας ολόκληρη την αγορά του ποταμού, στη ροή της, με όλες τις απροσδόκητες στροφές και εκπλήξεις. Η ικανότητα να παρατηρούνται οι συνεχείς αλλαγές στη ροή είναι καθήκον της αποτελεσματικής ανάλυσης της αγοράς και το αντίδοτο στον δογματισμό, τη μοιραία «ασθένεια» των εμπόρων. Η αγορά φαίνεται συχνά τόσο χαοτική όσο ο εσωτερικός μας κόσμος, το ρεύμα της συνείδησής μας. Για να βγάλουμε κάποιο νόημα από αυτό το χάος, πρέπει να ανακαλύψουμε την υποκείμενη δομή για την πραγματικότητα και την αγορά - μια υποστηρικτική δομή που αποκαλύπτει την τάξη που βρίσκεται κάτω από το χάος.

Η αγορά, ως πραγματικό φαινόμενο, είναι θεμελιωδώς άτακτη και ελεύθερη. Το χάος κυριαρχεί στην προβλεψιμότητα. Οι απλές γραμμικές προσεγγίσεις για τη διαπραγμάτευση στην αγορά δεν λειτουργούν. Η αγορά είναι ατελείωτα πολύπλοκη. Από το χάος γεννιέται πάντα μια ανώτερη τάξη, αλλά αυτή η τάξη προκύπτει αυθόρμητα και απρόβλεπτα. Όπως ο καιρός, οι αγορές μετοχών και εμπορευμάτων, καθώς και άλλα χαοτικά συστήματα, μπορούν να προκαλέσουν απρόβλεπτες συνέπειες με αμελητέες αλλαγές στις ποσότητες πολλαπλασιαζόμενες με την αντίδραση σε αυτές. Επί του παρόντος, οι παίκτες του χρηματιστηρίου χρησιμοποιούν μη γραμμικές μεθόδους στις επενδύσεις και τις συναλλαγές. Τα φράκταλ είναι τα νέα παιχνίδια της αγοράς. Τα φράκταλ είναι ένας τρόπος αυτοοργάνωσης των αγορών. Μια συγκεκριμένη οργάνωση φράκταλ δημιουργείται χρησιμοποιώντας μηχανισμούς που στην επιστήμη του χάους ονομάζονται ελκυστές.

Για να χρησιμοποιήσουμε τη σκέψη για να τακτοποιήσουμε τα πράγματα και να μάθουμε να κατανοούμε τι συμβαίνει, πρέπει πρώτα να βρούμε την υποκείμενη δομή της πραγματικότητας. Μια δομή που αποκαλύπτει την τάξη που βρίσκεται κάτω από το χάος. Υπάρχουν τέσσερις μη γραμμικές συναρτήσεις που μας βοηθούν να ορίσουμε αυτή τη σειρά στο μυαλό μας. Οι επιστήμονες που μελετούν το χάος ανακάλυψαν ότι οι φαινομενικά χαοτικές, παράνομες διαδικασίες ακολουθούν στην πραγματικότητα μια κρυφή σειρά. Η σειρά που ανακάλυψαν είναι τετραπλή: όλα τα εξωτερικά φαινόμενα ενεργούν σύμφωνα με αυτό που αποκαλούν τέσσερις ελκυστές - δυνάμεις που εξάγουν την τάξη από την αταξία. Ονομάζονται ο σημειακός ελκυστής, ο κυκλικός ελκυστής, ο ελκυστής του Θώρα και ο παράξενος ελκυστής.

Ένας ελκυστήρας σημείου είναι ο απλούστερος τρόπος για να φέρεις τάξη στο χάος. Ζει στην πρώτη διάσταση μιας γραμμής, η οποία αποτελείται από άπειρα σημεία. Υπό την επίδραση αυτού του ελκυστήρα, ένα άτομο βιώνει μια τάση για μια δραστηριότητα και μια αποστροφή για μια άλλη. Είναι ένας ελκυστήρας πρώτης διάστασης και μπορεί να χρησιμοποιηθεί για συναλλαγές σε αγορές.

Το χαρακτηριστικό ενός κυκλικού ελκυστήρα είναι να κινείται μπρος-πίσω, όπως ένα εκκρεμές ή ένας κυκλικός μαγνήτης. Ελκύει, μετά απωθεί, μετά έλκει ξανά κ.λπ. Ζει στη δεύτερη διάσταση του αεροπλάνου, που αποτελείται από άπειρο αριθμό γραμμών. Χαρακτηρίζει μια αγορά κλεισμένη σε ένα διάδρομο, όπου η τιμή κινείται πάνω-κάτω σε ένα συγκεκριμένο εύρος για μια συγκεκριμένη χρονική περίοδο. Αυτός ο ελκυστής είναι πιο περίπλοκος από τον ελκυστήρα σημείου και είναι η υποκείμενη δομή για πιο σύνθετη συμπεριφορά. Μια δραστηριότητα οδηγεί αυτόματα σε μια άλλη με επαναλαμβανόμενη σειρά. Στην αγορά σιτηρών το φαινόμενο αυτό είναι ετήσιο.

Ένας τρίτος, πιο σύνθετος τύπος ελκυστήρα είναι γνωστός ως ελκυστής Toras. Ξεκινά μια περίπλοκη κυκλοφορία που επαναλαμβάνεται καθώς προχωρά. Ζει στην τρίτη διάσταση, η οποία αποτελείται από έναν άπειρο αριθμό αεροπλάνων. Σε σύγκριση με τους κυκλικούς και σημειακούς ελκυστές, ο ελκυστής Toras εισάγει μεγαλύτερο βαθμό διαταραχής και τα μοντέλα του είναι πιο περίπλοκα. Σε αυτό το επίπεδο, οι προβλέψεις είναι πιο ακριβείς και τα μοντέλα τείνουν να φαίνονται πιο ολοκληρωμένα. Γραφικά μοιάζει με δαχτυλίδι ή κουλούρι. Σχηματίζει σπειροειδείς κύκλους σε πολλά διαφορετικά επίπεδα και μερικές φορές επιστρέφει μόνος του για να ολοκληρώσει μια πλήρη περιστροφή. Το κύριο χαρακτηριστικό του είναι η επαναλαμβανόμενη δράση. Παρόμοια φαινόμενα μπορούν επίσης να παρατηρηθούν στην αναζήτηση ασφάλειας από παγκόσμια περιουσιακά στοιχεία. Εάν το επιτόκιο των κρατικών τίτλων αυξηθεί, προσελκύουν περισσότερους επενδυτές. Στη συνέχεια οι τιμές τους ανεβαίνουν, γεγονός που μειώνει το επιτόκιο και τα καθιστά λιγότερο ελκυστικά κ.λπ.

Ένας παράξενος ελκυστής από την τέταρτη διάσταση αυτοοργανώνεται. Είναι η γενέτειρα της ελευθερίας και της κατανόησης του πώς λειτουργεί πραγματικά η αγορά. Αυτό που το επιφανειακό μάτι αντιλαμβάνεται ως απόλυτο χάος, στο οποίο δεν διακρίνεται καμία τάξη, έχει μια ορισμένη σειρά που βασίζεται σε έναν παράξενο ελκυστήρα όταν γίνεται παρατήρηση από την τέταρτη διάσταση. Ένα άλλο χαρακτηριστικό ενός παράξενου ελκυστήρα είναι η ευαισθησία στις αρχικές συνθήκες, που μερικές φορές ονομάζεται «φαινόμενο της πεταλούδας». Η παραμικρή απόκλιση από τις αρχικές συνθήκες μπορεί να οδηγήσει σε τεράστιες διαφορές στο αποτέλεσμα. Οι διαφορές στις αρχικές συνθήκες κατά τη σύναψη συναλλαγών μπορεί να επηρεάσουν την κερδοφορία ενός συστήματος συναλλαγών κατά πέντε φορές. Με άλλα λόγια, η λήψη συναλλαγών κάτω από ευαίσθητες αρχικές συνθήκες μπορεί να οδηγήσει σε αύξηση των κερδών κατά 500%.

Φράκταλ

Οι έννοιες της γεωμετρίας φράκταλ και φράκταλ, που εμφανίστηκαν στα τέλη της δεκαετίας του '70, έχουν καθιερωθεί σταθερά μεταξύ των μαθηματικών και των προγραμματιστών από τα μέσα της δεκαετίας του '80. Η λέξη fractal προέρχεται από το λατινικό fractus και σε μετάφραση σημαίνει κατακερματισμένη. Προτάθηκε από τον Benoit Mandelbrot το 1975 για να αναφερθεί στις ακανόνιστες αλλά όμοιες δομές με τις οποίες τον απασχολούσε. Η γέννηση της γεωμετρίας φράκταλ συνδέεται συνήθως με τη δημοσίευση του βιβλίου του Mandelbrot το 1977 «Η φράκταλ γεωμετρία της φύσης». Τα έργα του χρησιμοποίησαν τα επιστημονικά αποτελέσματα άλλων επιστημόνων που εργάστηκαν την περίοδο 1875-1925 στον ίδιο τομέα (Poincaré, Fatou, Julia, Cantor, Hausdorff). Αλλά μόνο στην εποχή μας κατέστη δυνατός ο συνδυασμός της δουλειάς τους σε ένα ενιαίο σύστημα.

Ο ρόλος των φράκταλ στα γραφικά υπολογιστών σήμερα είναι αρκετά μεγάλος. Έρχονται στη διάσωση, για παράδειγμα, όταν είναι απαραίτητο, χρησιμοποιώντας αρκετούς συντελεστές, για να ορίσουν γραμμές και επιφάνειες πολύ περίπλοκων σχημάτων. Από την άποψη των γραφικών υπολογιστών, η γεωμετρία φράκταλ είναι απαραίτητη κατά τη δημιουργία τεχνητών σύννεφων, βουνών και επιφανειών θάλασσας. Μάλιστα, έχει βρεθεί ένας τρόπος να αναπαριστούν εύκολα πολύπλοκα μη Ευκλείδεια αντικείμενα, οι εικόνες των οποίων μοιάζουν πολύ με τα φυσικά.

Μία από τις κύριες ιδιότητες των φράκταλ είναι η αυτο-ομοιότητα. Στην απλούστερη περίπτωση, ένα μικρό μέρος ενός φράκταλ περιέχει πληροφορίες για ολόκληρο το φράκταλ.

Ο ορισμός του φράκταλ του Mandelbrot είναι: «Ένα φράκταλ είναι μια δομή που αποτελείται από μέρη που κατά κάποια έννοια είναι παρόμοια με το σύνολο»

Φράκταλ:

Γεωμετρικά φράκταλ

Τα φράκταλ αυτής της κατηγορίας είναι τα πιο οπτικά. Στη δισδιάστατη περίπτωση, λαμβάνονται χρησιμοποιώντας κάποια διακεκομμένη γραμμή (ή επιφάνεια στην τρισδιάστατη περίπτωση), που ονομάζεται γεννήτρια. Σε ένα βήμα του αλγορίθμου, καθένα από τα τμήματα που συνθέτουν την πολύγραμμη αντικαθίσταται με μια πολυγραμμή γεννήτριας, στην κατάλληλη κλίμακα. Ως αποτέλεσμα της ατελείωτης επανάληψης αυτής της διαδικασίας, προκύπτει ένα γεωμετρικό φράκταλ.

Εικόνα 1. Κατασκευή της τριοδικής καμπύλης Koch.

Ας εξετάσουμε ένα από αυτά τα φράκταλ αντικείμενα - την τριοδική καμπύλη Koch. Η κατασκευή της καμπύλης ξεκινά με ένα τμήμα μοναδιαίου μήκους (Εικ. 1) - αυτή είναι η 0η γενιά της καμπύλης Koch. Στη συνέχεια, κάθε σύνδεσμος (ένα τμήμα στη μηδενική γενιά) αντικαθίσταται από διαμορφωτικό στοιχείο, που ορίζεται στο Σχ. 1 με n=1. Ως αποτέλεσμα αυτής της αντικατάστασης, προκύπτει η επόμενη γενιά της καμπύλης Koch. Στην 1η γενιά, είναι μια καμπύλη τεσσάρων ευθύγραμμων συνδέσμων, μήκους 1/3 ο καθένας. Για να αποκτήσετε την 3η γενιά, εκτελούνται οι ίδιες ενέργειες - κάθε σύνδεσμος αντικαθίσταται με ένα μειωμένο στοιχείο διαμόρφωσης. Έτσι, για να ληφθεί κάθε επόμενη γενιά, όλοι οι σύνδεσμοι της προηγούμενης γενιάς πρέπει να αντικατασταθούν με ένα μειωμένο στοιχείο διαμόρφωσης. Η καμπύλη nης γενιάς για οποιοδήποτε πεπερασμένο n ονομάζεται προφρακτικός. Το σχήμα 1 δείχνει πέντε γενιές της καμπύλης. Καθώς το n τείνει στο άπειρο, η καμπύλη Koch γίνεται φράκταλ αντικείμενο

Στα γραφικά υπολογιστών, η χρήση γεωμετρικών φράκταλ είναι απαραίτητη κατά τη λήψη εικόνων δέντρων, θάμνων και ακτών. Τα δισδιάστατα γεωμετρικά φράκταλ χρησιμοποιούνται για τη δημιουργία τρισδιάστατων υφών (μοτίβα στην επιφάνεια ενός αντικειμένου).

Αλγεβρικά φράκταλ

Αυτή είναι η μεγαλύτερη ομάδα φράκταλ. Λαμβάνονται με τη χρήση μη γραμμικών διεργασιών σε n-διάστατους χώρους. Οι δισδιάστατες διεργασίες είναι οι πιο μελετημένες. Κατά την ερμηνεία μιας μη γραμμικής επαναληπτικής διαδικασίας ως ένα διακριτό δυναμικό σύστημα, μπορεί κανείς να χρησιμοποιήσει την ορολογία της θεωρίας αυτών των συστημάτων: πορτρέτο φάσης, σταθερή διαδικασία, ελκυστήςκαι τα λοιπά.

Είναι γνωστό ότι τα μη γραμμικά δυναμικά συστήματα έχουν αρκετές σταθερές καταστάσεις. Η κατάσταση στην οποία βρίσκεται το δυναμικό σύστημα μετά από έναν ορισμένο αριθμό επαναλήψεων εξαρτάται από την αρχική του κατάσταση. Επομένως, κάθε σταθερή κατάσταση (ή, όπως λένε, ελκυστής) έχει μια συγκεκριμένη περιοχή αρχικών καταστάσεων, από τις οποίες το σύστημα θα πέσει αναγκαστικά στις τελικές καταστάσεις που εξετάζουμε. Έτσι, ο χώρος φάσης του συστήματος χωρίζεται σε περιοχές έλξηςελκυστές. Εάν ο χώρος φάσης είναι δισδιάστατος, τότε χρωματίζοντας τις περιοχές έλξης με διαφορετικά χρώματα, μπορεί κανείς να αποκτήσει πορτρέτο έγχρωμης φάσηςαυτό το σύστημα (επαναληπτική διαδικασία). Αλλάζοντας τον αλγόριθμο επιλογής χρώματος, μπορείτε να αποκτήσετε πολύπλοκα μοτίβα φράκταλ με παράξενα πολύχρωμα μοτίβα. Μια έκπληξη για τους μαθηματικούς ήταν η ικανότητα δημιουργίας πολύ περίπλοκων μη τετριμμένων δομών χρησιμοποιώντας πρωτόγονους αλγόριθμους.

Εικ. 3. Σετ Mandelbrot.

Ως παράδειγμα, λάβετε υπόψη το σύνολο Mandelbrot (βλ. Εικ. 3 και Εικ. 4). Ο αλγόριθμος για την κατασκευή του είναι αρκετά απλός και βασίζεται σε μια απλή επαναληπτική έκφραση:

όπου Zi και C είναι μιγαδικές μεταβλητές. Εκτελούνται επαναλήψεις για κάθε σημείο εκκίνησης C μιας ορθογώνιας ή τετράγωνης περιοχής - ένα υποσύνολο του μιγαδικού επιπέδου. Η επαναληπτική διαδικασία συνεχίζεται μέχρι να ξεπεράσει τον κύκλο της ακτίνας 2, το κέντρο του οποίου βρίσκεται στο σημείο (αυτό σημαίνει ότι ο ελκυστής του δυναμικού συστήματος βρίσκεται στο άπειρο) ή μετά από έναν αρκετά μεγάλο αριθμό επαναλήψεων (για παράδειγμα, 200 -500) συγκλίνει σε κάποιο σημείο του κύκλου. Ανάλογα με τον αριθμό των επαναλήψεων κατά τις οποίες παρέμεινε μέσα στον κύκλο, μπορείτε να ορίσετε το χρώμα του σημείου C (εάν παραμένει μέσα στον κύκλο για αρκετά μεγάλο αριθμό επαναλήψεων, η διαδικασία επανάληψης σταματά και αυτό το σημείο ράστερ βάφεται μαύρο).

Εικ. 4. Ένα τμήμα του ορίου του συνόλου Mandelbrot, μεγεθυσμένο κατά 200 φορές.

Ο παραπάνω αλγόριθμος δίνει μια προσέγγιση στο λεγόμενο σύνολο Mandelbrot. Το σύνολο Mandelbrot περιέχει σημεία που, κατά τη διάρκεια άπειροςο αριθμός των επαναλήψεων δεν πάει στο άπειρο (τα σημεία είναι μαύρα). Τα σημεία που ανήκουν στο όριο του συνόλου (εδώ προκύπτουν πολύπλοκες δομές) πηγαίνουν στο άπειρο σε έναν πεπερασμένο αριθμό επαναλήψεων και τα σημεία που βρίσκονται εκτός του συνόλου πηγαίνουν στο άπειρο μετά από πολλές επαναλήψεις (λευκό φόντο).

Στοχαστικά φράκταλ

Μια άλλη πολύ γνωστή κατηγορία φράκταλ είναι τα στοχαστικά φράκταλ, τα οποία προκύπτουν εάν κάποιες από τις παραμέτρους τους αλλάξουν τυχαία σε μια επαναληπτική διαδικασία. Σε αυτή την περίπτωση, τα αντικείμενα που προκύπτουν είναι πολύ παρόμοια με τα φυσικά - ασύμμετρα δέντρα, τραχιές ακτές κ.λπ. Τα δισδιάστατα στοχαστικά φράκταλ χρησιμοποιούνται στη μοντελοποίηση εδαφών και επιφανειών θάλασσας.

Υπάρχουν και άλλες ταξινομήσεις φράκταλ, για παράδειγμα, η διαίρεση των φράκταλ σε ντετερμινιστικά (αλγεβρικά και γεωμετρικά) και μη ντετερμινιστικά (στοχαστικά).

5. Ντετερμινιστικό χάος και πληροφορική

Κατ' αναλογία, στο φαινόμενο της ακανόνιστης (χαοτικής) κίνησης σε μη γραμμικά συστήματα δόθηκε ο όρος δυναμικός, ή ντετερμινιστική ,χάος.Η χαοτική συμπεριφορά που παρατηρείται δεν οφείλεται σε εξωτερικές πηγές θορύβου, ούτε λόγω του μεγάλου αριθμού βαθμών ελευθερίας, ούτε λόγω της αβεβαιότητας που σχετίζεται με την κβαντική μηχανική. Παράγεται από τη δυναμική ενός μη γραμμικού ντετερμινιστικού συστήματος. Στο χώρο φάσης του συστήματος, αυτή η συμπεριφορά αντιστοιχεί παράξενος ελκυστήρας. Ελκυστήρας (ελκυστής) μεταφρασμένο από τα αγγλικά σημαίνει «ελκυστήρας»· σε αυτήν την περίπτωση, αυτό είναι ένα σύνολο τροχιών στον χώρο φάσης προς τον οποίο έλκονται όλες οι άλλες τροχιές από μια συγκεκριμένη γειτονιά του ελκυστήρα, που ονομάζεται επίσης πισίνα έλξης. Ο όρος «παράξενο» χρησιμοποιείται για να τονίσει τις ασυνήθιστες ιδιότητες του ελκυστήρα που αντιστοιχούν σε χαοτική συμπεριφορά. Ο λόγος για την ακανόνιστη συμπεριφορά είναι η ιδιότητα των μη γραμμικών συστημάτων να διαχωρίζουν εκθετικά γρήγορα τις αρχικά κλειστές τροχιές σε μια περιορισμένη περιοχή του χώρου φάσης. Είναι αδύνατο να προβλεφθεί η συμπεριφορά των τροχιών των χαοτικών συστημάτων για μεγάλο χρονικό διάστημα, καθώς η ευαισθησία στις αρχικές συνθήκες είναι υψηλή και οι αρχικές συνθήκες, τόσο σε φυσικά πειράματα όσο και σε προσομοιώσεις υπολογιστή, μπορούν να ρυθμιστούν μόνο με πεπερασμένη ακρίβεια.

Διαχείριση Χάους

Με την πρώτη ματιά, η φύση του χάους αποκλείει τη δυνατότητα να το ελέγξουμε. Στην πραγματικότητα, η κατάσταση είναι ακριβώς το αντίθετο: η αστάθεια των τροχιών των χαοτικών συστημάτων τα καθιστά εξαιρετικά ευαίσθητα στον έλεγχο.

Ας υπάρχει, για παράδειγμα, ένα σύστημα με έναν περίεργο ελκυστήρα, και απαιτείται η μεταφορά της τροχιάς φάσης από το ένα σημείο του ελκυστήρα στο άλλο. Οι χαοτικές τροχιές έχουν την ιδιότητα να καταλήγουν σε μια γειτονιά με την πάροδο του χρόνου όποιοςσημείο που ανήκει στον ελκυστήρα. Εάν είναι απαραίτητο να συμβεί αυτό σε χρόνο όχι μεγαλύτερο από το T, το απαιτούμενο αποτέλεσμα μπορεί να επιτευχθεί μέσω μιας ή μιας σειράς λεπτών, ασήμαντων διαταραχών της τροχιάς. Κάθε μία από αυτές τις διαταραχές αλλάζει ελαφρώς μόνο την τροχιά. Αλλά μετά από κάποιο χρονικό διάστημα, η συσσώρευση και η εκθετική ενίσχυση μικρών διαταραχών οδηγεί σε μια αρκετά ισχυρή διόρθωση της τροχιάς. Με τη σωστή επιλογή των διαταραχών, αυτό καθιστά δυνατή την επίλυση του προβλήματος χωρίς να εκτρέπεται η τροχιά από τον χαοτικό ελκυστήρα. Έτσι, τα συστήματα με χάος επιδεικνύουν τόσο καλή δυνατότητα ελέγχου όσο και εκπληκτική πλαστικότητα: το σύστημα αντιδρά με ευαισθησία στις εξωτερικές επιρροές, διατηρώντας παράλληλα τον τύπο κίνησης. Ο συνδυασμός ελέγχου και πλαστικότητας, σύμφωνα με πολλούς ερευνητές, είναι ο λόγος για τον οποίο η χαοτική δυναμική είναι ένας χαρακτηριστικός τύπος συμπεριφοράς για πολλά ζωτικά υποσυστήματα ζωντανών οργανισμών. Για παράδειγμα, η χαοτική φύση του καρδιακού ρυθμού επιτρέπει στην καρδιά να ανταποκρίνεται ευέλικτα σε αλλαγές στο σωματικό και συναισθηματικό στρες, παρέχοντας ένα απόθεμα δυναμικής δύναμης.

Το χάος, όσο ενδιαφέρον κι αν είναι, είναι μόνο μέρος της σύνθετης συμπεριφοράς μη γραμμικά συστήματα. Υπάρχει επίσης ένα μη διαισθητικό φαινόμενο που θα μπορούσε να ονομαστεί αντι-χάος. Εκφράζεται στο γεγονός ότι ορισμένα πολύ διαταραγμένα συστήματα «κρυσταλλώνονται» αυθόρμητα, αποκτώντας υψηλό βαθμό τάξης. Το Antichaos υποτίθεται ότι παίζει σημαντικό ρόλο στη βιολογική ανάπτυξη και εξέλιξη.

Υπάρχουν πολλά επιχειρήματα υπέρ του γεγονότος ότι, μαζί με τους καλά μελετημένους τρεις τύπους συμπεριφοράς των δυναμικών συστημάτων - στατικές καταστάσεις, περιοδικές και ημιπεριοδικές ταλαντώσεις και χάος, υπάρχει και ένας τέταρτος, συγκεκριμένος τύπος συμπεριφοράς στα σύνορα. μεταξύ τακτικής κίνησης και χάους. Έχει σημειωθεί ότι σε αυτό το όριο, το οποίο ονομάζεται «άκρη του χάους», μπορούν να συμβούν διαδικασίες παρόμοιες με αυτές της εξέλιξης και της επεξεργασίας πληροφοριών.

Εικ1. Ένα παράδειγμα χρήσης της συνειρμικής μνήμης που βασίζεται στη χαοτική δυναμική για σκοπούς προσανατολισμού και πλοήγησης. Περιοχή προσανατολισμού συνολικής έκτασης 576 km 2 δίνεται από γεωγραφικό χάρτη σε κλίμακα Μ 1:20000. Χωρίζεται σε 16 θραύσματα, καθένα από τα οποία είναι μια έγχρωμη γραφική εικόνα με διαστάσεις 200x200 pixel σε αλφάβητο 256 χρωμάτων. Κάθε μία από τις εικόνες αναπαρίσταται ως οριακός κύκλος στην ίδια δισδιάστατη τμηματική γραμμική χαρτογράφηση.

Για να προσδιορίσει τη θέση, ο χρήστης χρειάζεται απλώς να παρουσιάσει οποιοδήποτε κομμάτι του τμήματος του χάρτη. Εάν η αναζήτηση ανά κομμάτι είναι επιτυχής (η επιτυχία καταγράφηκε όταν τεμάχια έως 1 km παρουσιάστηκαν στο πρόγραμμα 2 , δηλαδή έως και 0,2 τοις εκατό της αρχικής περιοχής), το αντίστοιχο τμήμα χάρτη θα εμφανιστεί στην οθόνη.

Το πρόγραμμα επιδεικνύει επίσης την ικανότητα αναγνώρισης από παραμορφωμένα κομμάτια. Στο παράδειγμά μας, το επίπεδο παραμόρφωσης στο κομμάτι που παρουσιάζεται για αναγνώριση μπορεί να είναι 70-80 τοις εκατό.

Σε αντίθεση με το δυναμικό χάος, το υπό εξέταση φαινόμενο, μερικές φορές ονομάζεται περίπλοκο(πολυπλοκότητα), εμφανίζεται σε συστήματα που αποτελούνται από πολλά αλληλεπιδρώντα στοιχεία. Τέτοια συστήματα συχνά όχι μόνο επιδεικνύουν τον τέταρτο τύπο συμπεριφοράς, αλλά έχουν και προσαρμοστικές ιδιότητες, εάν με τον όρο προσαρμογή εννοούμε μια απότομη απλοποίηση της δυναμικής συστήματασε σύγκριση με την πολυδιάστατη χαοτική δυναμική το σύνολο των μεμονωμένων στοιχείων του. Τα παρακάτω παραδείγματα αντικατοπτρίζουν μια σειρά από γενικές ιδιότητες συστημάτων στα όρια του χάους.

Το παιχνίδι της ζωής σε κυψελωτά αυτόματα

Το σύνολο κανόνων αυτού του κυψελωτού αυτόματου (δηλαδή οι παράμετροι του συστήματος) είναι τέτοιο ώστε η συμπεριφορά του να βρίσκεται σε μια στενή ζώνη μεταξύ των περιοχών σταθερότητας και χάους. Το σύστημα παρουσιάζει συμπεριφορά παρόμοια με τις διαδικασίες της «πραγματικής» ζωής. Επιπλέον, κατά την ανάλυση αντικειμένων όπως "ανεμόπτερα" και "καταπέλτες", αποδείχθηκε μαθηματικά η ισοδυναμία του παιχνιδιού "Life" με τη μηχανή Turing και, επομένως, αποδείχθηκε η παρουσία σε αυτό διεργασιών ισοδύναμων με καθολικούς υπολογισμούς.

Βιολογική εξέλιξη

Από τον Δαρβίνο, οι βιολόγοι βλέπουν την εξέλιξη ως μια διαδικασία φυσικής επιλογής. Ωστόσο, είναι πιθανό η βιολογική τάξη να αντανακλά εν μέρει την αυθόρμητη τάξη ενάντια στην οποία λειτουργούσε ο μηχανισμός της φυσικής επιλογής. Με άλλα λόγια, στη διαδικασία της εξέλιξης, δεν μπορούν να πραγματοποιηθούν όλοι οι συνδυασμοί στο χώρο των μορφολογικών χαρακτηριστικών, αλλά μόνο ένα συγκεκριμένο επιλεγμένο σύνολο «ελκυστών». Δηλαδή, είναι δύσκολο να περιμένει κανείς ότι είναι πιθανές τυχόν παραμορφώσεις. Επιπλέον, ένας τέτοιος μηχανισμός επιταχύνει σημαντικά τη διαδικασία της εξέλιξης. Περιορίζει απότομα το σύνολο των επιτρεπόμενων τροχιών κίνησης και, ως εκ τούτου, τον απαιτούμενο αριθμό «επαναλήψεων» για την εμφάνιση ενός συγκεκριμένου βιολογικού είδους. Μια αναλογία μεταξύ της ταχύτητας σύγκλισης των μεθόδων τυχαίας και διαβάθμισης αναζήτησης ενός άκρου είναι κατάλληλη εδώ: στην πρώτη περίπτωση, η αναζήτηση πραγματοποιείται σε ολόκληρη την περιοχή παραλλαγής των μεταβλητών και στη δεύτερη - μόνο κατά μήκος ενός ορισμένου τροχιά.

Από τη σκοπιά της βιολογίας, δεν είναι τόσο σημαντικό ποιοι τύποι ελκυστών πραγματοποιούνται στο χώρο των μορφολογικών δυνατοτήτων. Είναι σημαντικό οι ροές των τροχιών να «πέφτουν» σε ορισμένες περιορισμένες περιοχές, αναδεικνύοντας έτσι νησίδες δομικά σταθερών ειδών στο χώρο των μορφολογικών χαρακτηριστικών. Και οι ίδιοι οι ελκυστές μπορεί να είναι νεροχύτες, κύκλοι, παράξενοι ελκυστές κ.λπ.

Αυτοοργανωμένη κρισιμότητα

Ένα σύστημα με μεγάλο αριθμό αλληλεπιδρώντων στοιχείων εξελίσσεται φυσικά σε μια κρίσιμη κατάσταση, στην οποία ένα μικρό γεγονός μπορεί να οδηγήσει σε καταστροφή. Αν και σε σύνθετα συστήματα συμβαίνουν περισσότερα μικρά γεγονότα από καταστροφές, οι αλυσιδωτές αντιδράσεις όλων των κλιμάκων αποτελούν αναπόσπαστο μέρος της δυναμικής. Όπως προκύπτει από τη θεωρία της κρισιμότητας, τα μικρά γεγονότα προκαλούνται από τον ίδιο μηχανισμό με τα μεγάλα. Επιπλέον, τα συστατικά μέρη του συστήματος δεν φτάνουν ποτέ σε ισορροπία, αλλά αντ' αυτού εξελίσσονται από τη μια μετασταθερή κατάσταση στην άλλη.

Η έννοια της αυτοοργανωμένης κρισιμότητας προϋποθέτει ότι τα παγκόσμια χαρακτηριστικά, όπως ο σχετικός αριθμός μεγάλων και μικρών γεγονότων, είναι ανεξάρτητα από μικροσκοπικούς μηχανισμούς. Αυτός είναι ο λόγος για τον οποίο τα γενικά χαρακτηριστικά ενός συστήματος δεν μπορούν να γίνουν κατανοητά αναλύοντας τα μέρη του ξεχωριστά.

Πώς μπορεί κανείς να φανταστεί τον μηχανισμό προσαρμογής σε συζευγμένα δυναμικά συστήματα; Το μοντέλο της εξελικτικής ισορροπίας (η άκρη του χάους) ως ένα είδος χαοτικού συγχρονισμού φαίνεται δελεαστικό. Πράγματι, η διαδικασία συγχρονισμού απλοποιεί δραματικά τη δυναμική του συστήματος, μειώνοντας τη διάσταση του ελκυστήρα του. Καθορίζεται άμεσα από τον βαθμό συνδεσιμότητας του συστήματος - ο "προσαρμοστικός μηχανισμός" της κίνησης προς την άκρη του χάους ενεργοποιείται μόνο εάν υπάρχουν επαρκώς ισχυρές συνδέσεις.

Παραγωγή πληροφοριών από χαοτικά συστήματα

Ας επιστρέψουμε στις ιδιότητες του χάους σε συστήματα χαμηλών διαστάσεων. Έτσι, η συμπεριφορά των χαοτικών τροχιών δεν μπορεί να προβλεφθεί σε μεγάλα χρονικά διαστήματα. Η πρόβλεψη της κίνησης κατά μήκος των τροχιών γίνεται όλο και πιο αβέβαιη καθώς απομακρύνεται κανείς από τις αρχικές συνθήκες. Από την άποψη της θεωρίας της πληροφορίας, αυτό σημαίνει ότι το ίδιο το σύστημα παράγει πληροφορίες και όσο μεγαλύτερο είναι το χάος του συστήματος, τόσο μεγαλύτερος είναι ο ρυθμός δημιουργίας πληροφοριών. Εφόσον το σύστημα δημιουργεί πληροφορίες, οι τροχιές του συστήματος επίσης τις περιέχουν.

Ρύζι. 2.Ένα παράδειγμα χρήσης τεχνολογίας για αναζήτηση πληροφοριών σε μη δομημένα αρχεία κειμένων. Το κείμενο του βιβλίου "Winnie the Pooh and All-All-All" χρησιμοποιείται ως αρχείο. Σε απάντηση στην ερώτηση του Pooh, "Γιατί οι μέλισσες φτιάχνουν μέλι;" το σύστημα προσφέρει ένα κομμάτι κειμένου που περιέχει τη φράση: «Ο μόνος λόγος για να φτιάξω μέλι είναι για να μπορώ να το φάω».

Καταγραφή, αποθήκευση και ανάκτηση πληροφοριών χρησιμοποιώντας το χάος

Τώρα ας αναρωτηθούμε: είναι δυνατόν να συγκρίνουμε τις τροχιές του συστήματος με πληροφορίες με τη μορφή μιας ακολουθίας συμβόλων που μας ενδιαφέρουν; Εάν μπορούσε να γίνει αυτό, ορισμένες από τις τροχιές θα αντιστοιχούσαν στις αλληλουχίες πληροφοριών μας και θα μπορούσαν να ληφθούν λύνοντας τις εξισώσεις που καθορίζουν τη δυναμική του συστήματος. Εάν πάρετε οποιοδήποτε (όχι πολύ μικρό) τμήμα της ακολουθίας πληροφοριών, μπορείτε να το χρησιμοποιήσετε για να επαναφέρετε ολόκληρη την ακολουθία πληροφοριών που αντιστοιχεί σε μια δεδομένη τροχιά. Διαφορετικές αλληλουχίες πληροφοριών αντιστοιχούν σε διαφορετικές τροχιές και καθίσταται δυνατή η αποκατάσταση οποιασδήποτε από αυτές από οποιοδήποτε μικρό κομμάτι της. Αυτό παρέχει συσχετιστική πρόσβαση (πρόσβαση ανά περιεχόμενο) σε όλες τις πληροφορίες που καταγράφονται στο σύστημα. Έτσι, οι πληροφορίες απομνημονεύονται και αποθηκεύονται με τη μορφή τροχιών ενός δυναμικού συστήματος και έχουν ιδιότητες συσχέτισης.

Αυτή η ιδέα προέκυψε και αναπτύχθηκε σε προσπάθειες να κατανοηθεί πώς το χάος θα μπορούσε να είναι χρήσιμο στην επεξεργασία πληροφοριών από ζωντανά συστήματα. Κατασκευάστηκαν μαθηματικά μοντέλα που απέδειξαν τη θεμελιώδη δυνατότητα καταγραφής, αποθήκευσης και ανάκτησης πληροφοριών χρησιμοποιώντας τις τροχιές δυναμικών συστημάτων με χάος. Αυτά τα μοντέλα φαίνονταν πολύ απλά και ένας ειδικός από ένα έγκριτο διεθνές περιοδικό έγραψε στην κριτική του: «Αυτά είναι απλά μοντέλα παιχνιδιών και δεν μπορεί να δημιουργηθεί τεχνολογία στη βάση τους, είτε στην Ανατολή είτε στη Δύση. Ωστόσο, σύντομα η έρευνα προς αυτή την κατεύθυνση τιμήθηκε με το Μεγάλο Βραβείο στον διαγωνισμό αναγνώρισης προτύπων της εταιρείας Hewlett-Packard. Η ανάπτυξη των «παιχνιδιών» οδήγησε στο γεγονός ότι η δυνητική τους χωρητικότητα πληροφοριών υπερβαίνει σημαντικά τον όγκο όλων των πληροφοριών που είναι διαθέσιμες στο Διαδίκτυο (Δίπλωμα ευρεσιτεχνίας RF 2050072, ευρεσιτεχνία ΗΠΑ US 5774587). Και ακόμη και σε μέτρια "pisishki" κατέστη δυνατή η σύνθεση δυναμικών συστημάτων με όγκο καταγεγραμμένων πληροφοριών ισοδύναμο με τον μέσο όρο των έργων που συλλέγονται.

Ρύζι. 3.Μια πηγή χάους που αποτελείται από μη γραμμικά και γραμμικά συστήματα κλειστά σε έναν δακτύλιο ανάδρασης. Δεξιά: εξωτερική όψη της πλακέτας ηλεκτρονικού κυκλώματος (πάνω) και πορτρέτο φάσης ενός χαοτικού ελκυστήρα (κάτω). Ακόμη και μικρές αλλαγές στις παραμέτρους των στοιχείων του ηλεκτρονικού κυκλώματος οδηγούν σε σημαντική αλλαγή στη φύση των χαοτικών ταλαντώσεων.

Η ανεπτυγμένη τεχνολογία σάς επιτρέπει να καταγράψετε, να αποθηκεύσετε και να ανακτήσετε κάθε τύπο δεδομένων: εικόνες, κείμενα, ψηφιακή μουσική και ομιλία, σήματα κ.λπ. Ένα παράδειγμα χρήσης της τεχνολογίας είναι το σύστημα διαχείρισης εγγράφων προσωπικού φαξ με συσχετιστική πρόσβαση FacsData Wizard, το οποίο παρέχει τη δυνατότητα δημιουργίας αρχείων αδόμητων πληροφοριών με πλήρη αυτόματη ευρετηρίαση όλων των αποθηκευμένων πληροφοριών.

Για να αναζητήσει τα απαραίτητα έγγραφα, ο χρήστης συνθέτει ένα αίτημα πληκτρολογώντας σε ελεύθερη μορφή πολλές γραμμές κειμένου που σχετίζονται με το περιεχόμενο του απαιτούμενου εγγράφου. Σε απάντηση, το σύστημα θα παράσχει το απαιτούμενο έγγραφο εάν οι πληροφορίες εισόδου είναι επαρκείς για τη σαφή αναζήτησή του ή θα προσφέρει ένα σύνολο επιλογών. Εάν είναι απαραίτητο, μπορείτε επίσης να λάβετε ένα αντίγραφο φαξ του εγγράφου που βρέθηκε. Η παρουσία σφαλμάτων στο αίτημα και κατά τη μετατροπή πληροφοριών πηγής σε κείμενο δεν επηρεάζει σημαντικά την ποιότητα της αναζήτησης. Η δημιουργία ενός ηλεκτρονικού αρχείου δεν απαιτεί επιπλέον χώρο στο δίσκο. Ο χώρος που απαιτείται για την αποθήκευση εγγεγραμμένων εγγράφων μπορεί ακόμη και να μειωθεί.

Μεταφορά και προστασία πληροφοριών

Τα περισσότερα σύγχρονα συστήματα επικοινωνίας χρησιμοποιούν αρμονικές ταλαντώσεις ως φορέα πληροφοριών. Το σήμα πληροφοριών στον πομπό διαμορφώνει αυτές τις ταλαντώσεις σε πλάτος, συχνότητα ή φάση και στον δέκτη οι πληροφορίες διαχωρίζονται χρησιμοποιώντας την αντίστροφη λειτουργία - αποδιαμόρφωση. Η διαμόρφωση του φορέα μπορεί να πραγματοποιηθεί είτε διαμορφώνοντας ήδη σχηματισμένες αρμονικές ταλαντώσεις, είτε ελέγχοντας τις παραμέτρους της γεννήτριας κατά το σχηματισμό ταλαντώσεων.

Με παρόμοιο τρόπο, είναι δυνατή η διαμόρφωση ενός χαοτικού σήματος με ένα σήμα πληροφοριών. Ωστόσο, οι δυνατότητες εδώ είναι πολύ ευρύτερες. Πράγματι, εάν στην περίπτωση των αρμονικών σημάτων υπάρχουν μόνο τρία ελεγχόμενα χαρακτηριστικά (πλάτος, φάση και συχνότητα), τότε στην περίπτωση χαοτικών ταλαντώσεων ακόμη και μια μικρή αλλαγή στην παράμετρο δίνει σταθεροποιημένο με ασφάλειααλλαγή στη φύση των κραδασμών. Αυτό σημαίνει ότι οι πηγές χάους με μεταβλητές παραμέτρους έχουν ένα ευρύ φάσμα σχημάτων για την εισαγωγή ενός σήματος πληροφοριών σε ένα χαοτικό (δηλ. διαμόρφωση ενός χαοτικού σήματος με ένα πληροφοριακό). Επιπλέον, τα χαοτικά σήματα είναι βασικά ευρυζωνικά, το ενδιαφέρον για το οποίο είναι παραδοσιακό στη ραδιομηχανική και συνδέεται με μεγαλύτερη χωρητικότητα πληροφοριών. Στα συστήματα επικοινωνίας, χρησιμοποιείται μια ευρεία ζώνη συχνοτήτων φερόντων σημάτων τόσο για την αύξηση της ταχύτητας μετάδοσης πληροφοριών όσο και για την αύξηση της σταθερότητας της λειτουργίας του συστήματος παρουσία διαταραχών.

Πρόσφατα, λόγω της ανάπτυξης δορυφορικών, κινητών, κυψελωτών και οπτικών ινών συστημάτων επικοινωνίας πολλών χρηστών, σήματα εξάπλωσης φάσματος, όπου η ζώνη συχνοτήτων του μεταδιδόμενου σήματος μπορεί να είναι σημαντικά μεγαλύτερη από τη ζώνη συχνοτήτων του σήματος πληροφοριών.

Η φύση του θορύβου και ο αυτοσυγχρονισμός των συστημάτων που βασίζονται στο χάος τους δίνουν πιθανά πλεονεκτήματα έναντι των παραδοσιακών συστημάτων εξάπλωσης φάσματος που βασίζονται σε ψευδοτυχαίες ακολουθίες. Επιπλέον, επιτρέπουν απλούστερες υλοποιήσεις υλικού με μεγαλύτερη ενεργειακή απόδοση και υψηλότερες λειτουργικές ταχύτητες.

Ρύζι. 4.Ένα παράδειγμα ενός σχήματος επικοινωνίας που χρησιμοποιεί το χάος. Ο πομπός και ο δέκτης περιλαμβάνουν τα ίδια μη γραμμικά και γραμμικά συστήματα με την πηγή. Επιπλέον, ένας αθροιστής περιλαμβάνεται στον πομπό και ένας αφαιρετικός περιλαμβάνεται στον δέκτη. Στον αθροιστή, το χαοτικό σήμα πηγής και το σήμα πληροφοριών προστίθενται, και ο αφαιρετικός δέκτης έχει σχεδιαστεί για να διαχωρίζει το σήμα πληροφοριών. Το σήμα στο κανάλι μοιάζει με χάος και δεν περιέχει ορατά σημάδια των πληροφοριών που μεταδίδονται, γεγονός που καθιστά δυνατή τη μετάδοση εμπιστευτικών πληροφοριών. Σήματα σε σημεία ΕΝΑΚαι Α", ΒΚαι ΣΙ"κατά ζεύγη ίσο. Επομένως, παρουσία σήματος πληροφοριών εισόδου μικρόστην είσοδο του αθροιστή πομπού, το ίδιο σήμα θα εκχωρηθεί στην έξοδο του αφαιρέτη του δέκτη.

Το πεδίο εφαρμογής των χαοτικών σημάτων δεν περιορίζεται στα συστήματα εξάπλωσης φάσματος. Μπορούν να χρησιμοποιηθούν για την απόκρυψη μεταδιδόμενων πληροφοριών και χωρίςεπέκταση του φάσματος, δηλαδή όταν η ζώνη συχνοτήτων των πληροφοριών και των εκπεμπόμενων σημάτων συμπίπτει.

Όλα αυτά τόνωσαν την ενεργό έρευνα σε χαοτικά συστήματα επικοινωνίας. Μέχρι σήμερα, με βάση το χάος, έχουν προταθεί διάφορες προσεγγίσεις για την επέκταση του εύρους των σημάτων πληροφοριών, την κατασκευή αυτοσυγχρονιζόμενων δεκτών και την ανάπτυξη απλών αρχιτεκτονικών πομπών και δεκτών. Η ιδέα των περισσότερων από τις προτεινόμενες λύσεις βασίζεται στον συγχρονισμό από το «σκλάβο σύστημα» (δέκτη) του αρχικού αδιατάρακτου χαοτικού σήματος που παράγεται από το «κύριο σύστημα» (πομπός). Χρησιμοποιώντας τέτοια σχήματα επικοινωνίας, τόσο οι αναλογικές όσο και οι ψηφιακές πληροφορίες μπορούν να μεταδοθούν με διαφορετικούς ρυθμούς ροής πληροφοριών και διαφορετικούς βαθμούς εμπιστευτικότητας. Ένα άλλο πιθανό πλεονέκτημα των σχημάτων επικοινωνίας χάους είναι η δυνατότητα εφαρμογής νέων τεχνικών κοινής χρήσης καναλιών, η οποία είναι ιδιαίτερα σημαντική σε συστήματα επικοινωνίας πολλών χρηστών.

Αν μέχρι πρόσφατα το πρόβλημα μυστικότηταμεταφορά πληροφοριών και το ευρύτερο πρόβλημα προστασία πληροφοριώναφορούσαν κυρίως στρατιωτικές και ειδικές εφαρμογές, τώρα η αγορά για μη στρατιωτικές εφαρμογές γίνεται όλο και πιο σημαντική. Παραδείγματα περιλαμβάνουν την προστασία εμπορικών πληροφοριών σε υπολογιστές και δίκτυα υπολογιστών, την ασφάλεια των ηλεκτρονικών πληρωμών, την προστασία από την πειρατεία CD-ROM, δίσκων μουσικής και βίντεο, προστασία αντιγραφής μουσικής, βίντεο και άλλων πληροφοριών που διανέμονται μέσω δικτύων υπολογιστών, τηλεφωνία Διαδικτύου κ.λπ. .

Η προστασία των εμπορικών πληροφοριών υπόκειται σε απαιτήσεις που διαφέρουν σημαντικά από τις «κλασικές». Ειδικότερα, η δυνατότητα μαζικής εφαρμογής και το χαμηλό κόστος ανά μονάδα προϊόντων «πληροφοριών» γίνονται τυπική απαίτηση. Επιπλέον, οι προσεγγίσεις προστασίας μπορεί να αλλάξουν. Έτσι, για την προστασία των πληροφοριών μουσικής και βίντεο σε CD από πειρατική αντιγραφή, δεν χρειάζεται οι εγγεγραμμένες πληροφορίες να είναι εντελώς απρόσιτες σε έναν «επιτιθέμενο»: αρκεί απλώς να μειώσετε την ποιότητα αναπαραγωγής σε επίπεδο απαράδεκτο για τον καταναλωτή.

Κατά την επίλυση τέτοιων «καθημερινών» προβλημάτων ασφάλειας πληροφοριών, στο μέλλον μπορούν να χρησιμοποιηθούν επιτυχώς μέσα που βασίζονται στο ντετερμινιστικό χάος.

Φυσικά, συγκεκριμένα παραδείγματα εφαρμογής του χάους στις τεχνολογίες πληροφοριών και επικοινωνιών που δίνονται στο άρθρο αντικατοπτρίζουν πρωτίστως τα επιστημονικά ενδιαφέροντα και απόψεις του συγγραφέα και της ομάδας στην οποία εργάζεται. Ταυτόχρονα, δίνουν μια ιδέα για το πώς, με τη βοήθεια χάοςδημιουργικά προβλήματα μπορούν να λυθούν.

6. Χάος σε άλλες επιστήμες

Η θεωρία του χάους έχει εφαρμογές σε ένα ευρύ φάσμα επιστημών. Μία από τις παλαιότερες ήταν η εφαρμογή του στην ανάλυση των αναταράξεων σε υγρά. Η κίνηση του υγρού είναι είτε στρωτή (ομαλή και κανονική) είτε τυρβώδης (σύνθετη και ακανόνιστη). Πριν από την εμφάνιση της θεωρίας του χάους, υπήρχαν δύο ανταγωνιστικές θεωρίες αναταράξεων. Το πρώτο από αυτά αντιπροσώπευε τις αναταράξεις ως συσσώρευση ολοένα και περισσότερων περιοδικών κινήσεων. το δεύτερο εξήγησε την αδυναμία εφαρμογής του τυπικού φυσικού μοντέλου από την αδυναμία περιγραφής ενός υγρού ως συνεχούς μέσου σε μοριακή κλίμακα. Το 1970, οι μαθηματικοί D. Ruel και F. Takens πρότειναν μια τρίτη εκδοχή: οι αναταράξεις είναι χάος σε ένα υγρό. Η υπόθεσή τους θεωρήθηκε αρχικά πολύ αμφιλεγόμενη, αλλά έκτοτε επιβεβαιώθηκε για αρκετές περιπτώσεις, ιδιαίτερα για τα πρώτα στάδια της ανάπτυξης αναταράξεων σε μια ροή μεταξύ δύο περιστρεφόμενων κυλίνδρων. Οι προχωρημένες αναταράξεις παραμένουν ένα μυστηριώδες φαινόμενο, αλλά το χάος είναι απίθανο να αποφευχθεί σε οποιαδήποτε πιθανή εξήγηση. (υδροαερομηχανική)

Η κίνηση στο ηλιακό σύστημα είναι επίσης γνωστό ότι είναι χαοτική, αλλά χρειάζονται δεκάδες εκατομμύρια χρόνια πριν οποιαδήποτε αλλαγή γίνει απρόβλεπτη. Το χάος εκδηλώνεται με πολλούς τρόπους. Για παράδειγμα, ο δορυφόρος του Κρόνου Hyperion περιφέρεται σε μια κανονική, προβλέψιμη τροχιά γύρω από τον πλανήτη του, αλλά την ίδια στιγμή πέφτει χαοτικά, αλλάζοντας την κατεύθυνση του δικού του άξονα περιστροφής. Η θεωρία του χάους εξηγεί αυτή την πτώση ως παρενέργεια των παλιρροϊκών δυνάμεων που δημιουργούνται από τον Κρόνο. Η θεωρία του χάους εξηγεί επίσης την κατανομή των σωμάτων στη ζώνη των αστεροειδών μεταξύ του Άρη και του Δία. Είναι ανομοιόμορφο: σε ορισμένες αποστάσεις από τον Ήλιο υπάρχουν συμπυκνώσεις, σε άλλες υπάρχουν κενά κενά. Τόσο οι συμπυκνώσεις όσο και οι κενοί χώροι των ηλιοκεντρικών τροχιών τους βρίσκονται σε αποστάσεις που σχηματίζουν «συντονισμούς» με τον Δία. Η θεωρία του χάους δείχνει ότι ορισμένοι συντονισμοί παράγουν σταθερή συμπεριφορά (συστάδες), ενώ άλλοι παράγουν ασταθή συμπεριφορά (κενά κενά).

Το χάος εμφανίζεται επίσης στη βιολογία και την οικολογία. Στα τέλη του 19ου αιώνα. Έχει βρεθεί ότι οι πληθυσμοί των ζώων είναι σπάνια σταθεροί. χαρακτηρίζονται από ακανόνιστα εναλλασσόμενες περιόδους ταχείας ανάπτυξης και σχεδόν πλήρους εξαφάνισης. Η θεωρία του χάους δείχνει ότι απλοί νόμοι του μεγέθους του πληθυσμού μπορούν να εξηγήσουν αυτές τις διακυμάνσεις χωρίς να εισάγουν τυχαίες εξωτερικές επιρροές. Η θεωρία του χάους εξηγεί επίσης τη δυναμική των επιδημιών, δηλ. κυμαινόμενοι πληθυσμοί μικροοργανισμών στο ανθρώπινο σώμα.

Μπορεί να φαίνεται ότι η θεωρία του χάους δεν πρέπει να έχει χρήσιμες εφαρμογές, καθώς τα χαοτικά συστήματα είναι απρόβλεπτα. Ωστόσο, αυτό είναι εσφαλμένο, πρώτον, επειδή μόνο ορισμένες πτυχές των χαοτικών συστημάτων είναι απρόβλεπτες, και δεύτερον, επειδή η χρησιμότητα της θεωρίας δεν περιορίζεται στην ικανότητά της να προβλέπει άμεσα. Μεταξύ των πιο ελπιδοφόρων εφαρμογών της θεωρίας του χάους είναι ο «χαοτικός έλεγχος». Το 1950, ο J. von Neumann πρότεινε ότι η αστάθεια του καιρού θα μπορούσε μια μέρα να αποδειχθεί καλό, αφού η αστάθεια σήμαινε ότι το επιθυμητό αποτέλεσμα θα μπορούσε να επιτευχθεί με πολύ μικρή διαταραχή. Το 1990, οι S. Grebogi, E. Ott και J. York δημοσίευσαν ένα θεωρητικό σχήμα για τη χρήση αυτού του τύπου αστάθειας για τον έλεγχο των χαοτικών συστημάτων. Το διάγραμμά τους είναι μια γενική μορφή της μεθόδου με την οποία οι μηχανικοί της NASA έστειλαν ένα διαστημικό ανιχνευτή για ραντεβού με τον κομήτη Giacobini-Zinner το 1985. Ο ανιχνευτής έκανε κύκλους γύρω από τη Σελήνη πέντε φορές, χρησιμοποιώντας τη χαοτική αλληλεπίδραση τριών σωμάτων, η οποία του επιτρέπει να κάνει μεγάλες αλλαγές στην τροχιά με χαμηλή κατανάλωση καυσίμου. Η ίδια μέθοδος εφαρμόστηκε για τον συγχρονισμό μιας μπαταρίας λέιζερ. για τον έλεγχο των ανωμαλιών του καρδιακού παλμού, γεγονός που ανοίγει τη δυνατότητα δημιουργίας ενός «έξυπνου» διεγέρτη καρδιακού ρυθμού. για τον έλεγχο των βιορευμάτων του εγκεφάλου, τα οποία, ειδικότερα, μπορούν να βοηθήσουν στον έλεγχο των επιληπτικών κρίσεων· τέλος, για στρωματοποίηση της τυρβώδους ροής ρευστού - μια μέθοδος που μπορεί να μειώσει την κατανάλωση καυσίμου από τα αεροσκάφη.

Βρετανοί φυσικοί έχουν δημιουργήσει ένα σύστημα που φέρνει τάξη στο χάος

Βρετανοί φυσικοί από το Πανεπιστήμιο του Warwick ανέπτυξαν μια μέθοδο που τους επιτρέπει να προβλέψουν την εμφάνιση της τάξης από το χάος σε πολύπλοκα συστήματα που αποτελούνται από πολλά τυχαία μεταβαλλόμενα στοιχεία.

Οι επιστήμονες με επικεφαλής τον Robert Weeks κατά τη διάρκεια της έρευνάς τους προσπάθησαν να καταλάβουν πώς πολύπλοκα συστήματα όπως το πλάσμα, τα πλήθη ανθρώπων ή τα σμήνη πουλιών μετακινούνται ξαφνικά από το χάος στην τάξη χωρίς εξωτερική παρέμβαση.

Οι ειδικοί έχουν προτείνει ότι τα πρότυπα αυτοοργάνωσης μπορεί να είναι τα ίδια για διαφορετικά πολύπλοκα συστήματα. Ως εκ τούτου, χρησιμοποιώντας ως βάση γνωστά δεδομένα για τη συμπεριφορά μεγάλων ομάδων ζώων και εντόμων, ανέπτυξαν μια νέα μαθηματική μέθοδο ανάλυσης που ονομάζεται μέθοδος αμοιβαίας πληροφόρησης.

Αυτή η νέα μέθοδος μπορεί να εντοπίσει μοτίβα και συσχετισμούς από πολύ λίγα δεδομένα. Για να δοκιμάσουν τη μέθοδό τους, οι ερευνητές χρησιμοποίησαν ένα απλό μοντέλο που αναπτύχθηκε τη δεκαετία του '90 από τον διάσημο Ούγγρο βιοφυσικό Tamás Wiček για να περιγράψει τη συμπεριφορά βακτηριακών αποικιών, κοπαδιών ψαρονιών ή ακρίδων.

Ως αποτέλεσμα, η νέα μέθοδος αμοιβαίας πληροφόρησης βρέθηκε να είναι τέσσερις φορές πιο ακριβής στην εύρεση μιας τακτοποιημένης κατάστασης από τις παραδοσιακές στατιστικές μεθόδους.

Οι επιστήμονες προτείνουν ότι η νέα μέθοδος θα είναι χρήσιμη και στη μελέτη του χρηματιστηρίου. Πιθανότατα θα είναι σε θέση να εξηγήσει τις μερικές φορές απροσδόκητες συσχετίσεις που προκύπτουν όταν οι μετοχές εταιρειών που δεν έχουν ορατές συνδέσεις αντιμετωπίζουν τις ίδιες διακυμάνσεις τιμών.

Οι μαθηματικοί έχουν υπολογίσει τη βέλτιστη στρατηγική για την καταπολέμηση της επιδημίας

Αμερικανοί και Ισραηλινοί μαθηματικοί έχουν υπολογίσει τη βέλτιστη στρατηγική για την καταπολέμηση της επιδημίας χρησιμοποιώντας εμβολιασμό.

Παραδοσιακά πιστεύεται ότι ο καλύτερος τρόπος για την καταπολέμηση της νόσου είναι να εμβολιαστούν όσο το δυνατόν περισσότερα άτομα. Σε μια νέα μελέτη, οι επιστήμονες διαπίστωσαν ότι αυτό δεν συμβαίνει. Εάν η επιδημία θεωρηθεί ως μια δυναμική διαδικασία, τότε ο χρόνος του εμβολιασμού αποδεικνύεται ότι δεν είναι λιγότερο σημαντικός από τον αριθμό των εμβολιασμένων ατόμων.

Χρησιμοποιώντας ένα πιθανό μοντέλο για να περιγράψουν τις διαδικασίες μόλυνσης, επαναμόλυνσης και εξάπλωσης της νόσου, οι επιστήμονες μπόρεσαν να προσδιορίσουν ότι, δεδομένης μιας σταθερής διαθέσιμης ποσότητας εμβολίου, η καλύτερη στρατηγική ήταν η διεξαγωγή μιας σειράς εντατικών εκδηλώσεων εμβολιασμού. Αποδείχθηκε ότι μια τέτοια σειρά λειτουργεί πιο αποτελεσματικά από έναν μόνο μαζικό εμβολιασμό.

Σύμφωνα με τους επιστήμονες, η αποτελεσματικότητα της στρατηγικής οφείλεται στο γεγονός ότι για μεγάλο χρονικό διάστημα ο αριθμός των μολυσμένων ατόμων σε μια ομάδα μπορεί να παραμείνει αρκετά σταθερός. Ο συνεπής εμβολιασμός σας επιτρέπει να μειώσετε έναν σταθερό αριθμό ασθενών και οδηγεί σε εκθετική μείωση του αριθμού των ασθενών.

Οι επιστήμονες τονίζουν ότι το μοντέλο τους δεν συνδέεται με κάποια συγκεκριμένη ασθένεια και μπορεί να εφαρμοστεί στην πιο γενική περίπτωση. Η κύρια δυσκολία σε αυτή την περίπτωση παραμένει ο υπολογισμός των περιόδων με τις οποίες πρέπει να γίνει ο εμβολιασμός.

Αλγόριθμοι μυρμηγκιών σε δράση

Το Εθνικό Εργαστήριο Βορειοδυτικού Ειρηνικού βρήκε μια νέα προσέγγιση για την ανάλυση της ασφάλειας των δικτύων υπολογιστών. Προτείνεται η χρήση «αλγόριθμων μυρμηγκιών» για την καταπολέμηση κακόβουλου λογισμικού.

Χρησιμοποιώντας ένα πρόγραμμα του οποίου οι αλγόριθμοι αντιγράφουν τους μηχανισμούς συμπεριφοράς των μυρμηγκιών, το εργαστήριο προσπαθεί να βρει «ανωμαλίες δικτύου».

«Τα μυρμήγκια από μόνα τους δεν είναι έξυπνα», λέει ο Glenn Fink, ο οποίος ηγήθηκε της ασυνήθιστης έρευνας, «αλλά μια αποικία μυρμηγκιών μπορεί να παρουσιάσει εκπληκτικά έξυπνη συμπεριφορά».

Σύμφωνα με τους επιστήμονες, το πρόγραμμά τους χρησιμοποιεί αισθητήρες που διανέμονται σε δίκτυα υπολογιστών που συλλέγουν συνεχώς δεδομένα. Όπως τα μυρμήγκια που μεταδίδουν πληροφορίες για φαγητό ή κίνδυνο στους συγγενείς τους χρησιμοποιώντας οσμές, αυτοί οι αισθητήρες μοιράζονται τις πληροφορίες που συλλέγουν μεταξύ τους. Έτσι, το πρόγραμμα μπορεί να εντοπίσει συγκεκριμένες ανωμαλίες δικτύου που σηματοδοτούν έναν πιθανό κίνδυνο, για παράδειγμα, μια μεγάλης κλίμακας μόλυνση του δικτύου.

Οι αισθητήρες έρχονται σε διάφορους προσανατολισμούς—σύμφωνα με τον Fink, ορισμένοι μπορούν να συλλέγουν δεδομένα σχετικά με το υπερβολικό φορτίο της CPU σε υπολογιστές, ενώ άλλοι μπορούν να ελέγχουν την κυκλοφορία δικτύου. Υπάρχουν επίσης «φρουροί» - ειδικά μπλοκ προγράμματος που αναλύουν πληροφορίες που λαμβάνονται από όλους τους αισθητήρες μυρμηγκιών.

Αν και το καινοτόμο σύμπλεγμα προστασίας από ιούς βρίσκεται σε πρώιμο στάδιο ανάπτυξης, είναι ήδη ικανό να ανιχνεύει ορισμένα σκουλήκια υπολογιστών. Ωστόσο, σύμφωνα με τους δημιουργούς, η τεχνητή νοημοσύνη του προγράμματός τους έχει ακόμα πολλά να μάθει.

Ωστόσο, σύμφωνα με τα παραπάνω, δεν προκύπτει ότι η θεωρία του χάους δεν έχει εφαρμογές στην πραγματική ζωή.

Τα Fractals είναι παντού, κυρίως σε προγράμματα γραφικών, όπως η εξαιρετικά επιτυχημένη σειρά προϊόντων Fractal Design Painter. Οι τεχνικές συμπίεσης δεδομένων φράκταλ εξακολουθούν να αναπτύσσονται, αλλά υπόσχονται εκπληκτικά αποτελέσματα, όπως αναλογίες συμπίεσης 600:1. Η βιομηχανία ειδικών εφέ ταινιών θα είχε πολύ λιγότερο ρεαλιστικά στοιχεία τοπίου (σύννεφα, βράχοι και σκιές) χωρίς την τεχνολογία φράκταλ γραφικών. Σήμερα, η αναζήτηση ερευνητών -κυρίως μαθηματικών- στοχεύει στον εντοπισμό όλων των τύπων μη γραμμικών εξισώσεων, η επίλυση των οποίων οδηγεί σε ντετερμινιστικό χάος. Το ενεργό ενδιαφέρον για αυτό προκαλείται από το γεγονός ότι τα ίδια μοτίβα μπορούν να εκδηλωθούν σε μια μεγάλη ποικιλία φυσικών φαινομένων και τεχνικών διαδικασιών: αναταράξεις στις ροές, αστάθεια ηλεκτρονικών και ηλεκτρικών δικτύων, αλληλεπίδραση ειδών στη ζωντανή φύση, χημικές αντιδράσεις, ακόμη και -προφανώς, στην ανθρώπινη κοινωνία. Αυτό συνεπάγεται τη θεμελιώδη σημασία του χάους - η μελέτη του μπορεί να οδηγήσει στη δημιουργία μιας ισχυρής μαθηματικής συσκευής με μεγάλη γενικότητα και εκτεταμένες δυνατότητες για εφαρμογές. Η θεωρία του χάους ακολουθεί τη δική της ιδιαίτερη διαδρομή από τα θεμέλια. Ίσως αυτός είναι ένας νέος, ανεξάρτητος δρόμος για την κατανόηση της οικουμενικότητας του κόσμου!

Βιβλιογραφία

1. Peitgen H. O., Richter P. H. «Η ομορφιά των φράκταλ».

2. V. I. Kuvshinov, A. V. Kuzmin «Πεδία μέτρησης και η θεωρία του ντετερμινιστικού χάους»

3. Shuster G. «Ντετερμινιστικό χάος: εισαγωγή».

4. Ruel D. "Randomness and Chaos." – Izhevsk: Επιστημονικό Κέντρο Ερευνών, 2001, 192 σελίδες.

5. Kronover R.M. «Φράκταλ και χάος σε δυναμικά συστήματα. Βασικές αρχές της Θεωρίας».

6. Magnitsky N. A., Sidorov S. V. «Νέες μέθοδοι χαοτικής δυναμικής». - M.: Editorial URSS, 2004, 320 p.

Αντίγραφο

1 Richard M. Kronover FRACTALS ΚΑΙ ΧΑΟΣ ΣΕ ΔΥΝΑΜΙΚΑ ΣΥΣΤΗΜΑΤΑ. ΒΑΣΗ ΘΕΩΡΙΑΣ. Μετάφραση από τα αγγλικά των T. E. Krenkel και A. L. Soloveichik, επιμέλεια T. E. Krenkel Προτείνεται από την UMO στον τομέα των ηλεκτρονικών και των εφαρμοσμένων μαθηματικών ως εγχειρίδιο για μαθητές με ειδικότητα στα «Εφαρμοσμένα Μαθηματικά» POSTMARKET ΜΟΣΧΑ 2000

2 P. M. Kronover. Φράκταλ και χάος σε δυναμικά συστήματα. Βασικά στοιχεία της θεωρίας. Μόσχα: Postmarket, σελ. Κριτές: Τμήμα Θεωρίας Πιθανοτήτων και Εφαρμοσμένων Μαθηματικών, Τεχνικό Πανεπιστήμιο Επικοινωνιών και Πληροφορικής της Μόσχας. Καθηγητής B. Yu. Sternin. Το πρώτο πλήρες εγχειρίδιο για τη νέα, ταχέως αναπτυσσόμενη μαθηματική πειθαρχία έχει μέχρι στιγμής εκδοθεί μόνο στα ρωσικά ως μονογραφίες. Καλά επιλεγμένες ασκήσεις και αλγόριθμοι καθιστούν το βιβλίο ένα εξαιρετικό εργαλείο για προπτυχιακούς και μεταπτυχιακούς φοιτητές, ειδικούς στις εφαρμογές αυτής της θεωρίας σε διάφορους τομείς από τη βιολογία έως τη γλωσσολογία. Εισαγωγή στα Φράκταλ και το Χάος Richard M. Crownover University of Missouri-Columbia Jones and Bartlett Publishers Boston London ORIGINAL ENGLISH LANGUAGE EDITION PUBLISHED BY Jones and Bartlett Publishers, Inc. 40 Tall Pine Drive, Sudbury, MA ΠΝΕΥΜΑΤΙΚΑ ΔΙΚΑΙΩΜΑΤΑ 1995 ALL RIGHTS RESERVED 1999 Μετάφραση στα ρωσικά, ZAO Postmarket Enterprise ISBN

3 Περιεχόμενα Πρόλογος 5 1. Εισαγωγή Τι είναι τα φράκταλ και το χάος; Υπόβαθρο t Κλασικά fractals Αυτο-ομοιότητα του συστήματος L-σύστημα Cantor dust Peano καμπύλες Σύνολα και αντιστοιχίσεις Προκαταρκτικά από τη θεωρία συνόλων Μετρικοί χώροι Συμπιεστικές αντιστοιχίσεις Μετασχηματισμοί συγγενών Hausdorff Metric I Συστήματα επαναλαμβανόμενων συναρτήσεων Συστήματα επαναλαμβανόμενων συναρτήσεων Υλοποίηση SIF SIF με διαστάσεις Dimenwskill Υπολογισμός διάστασης Χαοτική δυναμική I Ελκυστής Lorentz Επαναλαμβανόμενες αντιστοιχίσεις Feigenbaum καθολικότητα Sharkovsky περιοδικότητα Χάος 169

4 4 Περιεχόμενα 7. Χαοτική δυναμική II Ουσιαστική εξάρτηση Συμβολική δυναμική Χάος και φράκταλ Ανύψωση Σκίαση Τυχαιοποιημένος αλγόριθμος SIF Σύνθετη δυναμική Η Julia θέτει Τροχιές σε σύνολα Julia Σύνολο Mandelbrot Chaos και Julia σύνολα Κίνηση Πρόβλημα Cayley Τυχαία κλασματικά μετατόπιση Brownplacenndom και FBD 27S 9.6. Ανάλυση Fourier FBD Φιλτράρισμα Fourier 28S A. Πρόσθετες πληροφορίες από την ανάλυση 297 AL. Πληρότητα και συμπαγές 297 Α.2. Συνεχείς χαρτογραφήσεις ΖΩΣ Α.Ζ. Hausdorff metric II SOE A.4. Τοπολογική διάσταση 311 Α.5. Διάσταση Hausdorff 317 Α.6. Γρήγορος μετασχηματισμός Fourier 32C B. Θεωρία επανακανονικοποίησης και φράκταλ Poincaré 32E B.1. Θεωρία επανακανονικοποίησης 321 Β.2. Poincaré fractals ZZS Αναφορές 341 Ευρετήριο θεμάτων 34

5 Πρόλογος Φαίνεται ότι δύο τόσο διαφορετικά μαθηματικά αντικείμενα όπως τα φράκταλ και το χάος θα πρέπει να μελετώνται ανεξάρτητα το ένα από το άλλο: τελικά, η θεωρία των φράκταλ βασίζεται στη γεωμετρία και τη θεωρία των διαστάσεων και η θεωρία του χάους είναι μια ανάπτυξη του θεωρία δυναμικών συστημάτων. Από την άλλη, υπάρχει μια ορισμένη σχέση μεταξύ τους, η οποία συχνά χάνεται στις λεπτομέρειες της παρουσίασης καθεμιάς από τις θεωρίες. Αυτό το βιβλίο, πρώτον, είναι ένα εισαγωγικό μάθημα στη θεωρία των φράκταλ και τη θεωρία του χάους, και δεύτερον, εξετάζει το ερώτημα πώς ορισμένα φράκταλ (ελκυστές συστημάτων επαναλαμβανόμενων συναρτήσεων) μπορούν να δημιουργήσουν χάος. Τα κεφάλαια 2-5 καλύπτουν μια σειρά από σημαντικές ιδέες και έννοιες που σχετίζονται με ντετερμινιστικά φράκταλ: αυτο-ομοιότητα, επαναλαμβανόμενα συστήματα συναρτήσεων και διάσταση. Εδώ περιγράφονται επίσης συστήματα L, η χρήση των οποίων διευκολύνει πολύ τη γραφική κατασκευή, ειδικά στην περίπτωση φράκταλ που μοιάζουν με φυτά σε σχήμα. Η παρουσίαση της θεωρίας του ντετερμινιστικού χάους χωρίζεται σε δύο κεφάλαια. Το Κεφάλαιο 6, «Χαοτική Δυναμική Ι», εισάγει το θέμα σε στοιχειώδες επίπεδο, με περίπλοκες έννοιες όπως η συμβολική δυναμική που καλύπτονται κυρίως μέσω παραδειγμάτων. Το Κεφάλαιο 7, «Χαοτική Δυναμική του Ι», προορίζεται σε μεγάλο βαθμό για μαθητές με καλό μαθηματικό υπόβαθρο και μπορεί να παραλειφθεί εάν το μάθημα προορίζεται να απλοποιηθεί. Από την άλλη πλευρά, εδώ εκδηλώνεται η προαναφερθείσα σχέση μεταξύ φράκταλ και χάους. Το Κεφάλαιο 8, «Complex Dynamics», για τα σύνολα Julia και Mandelbrot, είναι γραμμένο σε απλοποιημένο στυλ. Τα αποτελέσματα που βασίζονται σε μιγαδικά θεωρήματα από τη θεωρία των συναρτήσεων μιας μιγαδικής μεταβλητής δεν αποδεικνύονται, αλλά επισημαίνονται σωστά και χρησιμοποιούνται εντατικά. Εκτός από τα αποτελέσματα της θεωρίας των συναρτήσεων μιας μιγαδικής μεταβλητής, η παρουσίαση καλύπτει πολλά σημαντικά ερωτήματα, για παράδειγμα, το ερώτημα εάν το σύνολο Julia είναι συνδεδεμένο ή εντελώς ασυνεχές, η απάντηση στο οποίο δίνεται από το σύνολο Mandelbrot.

6 6 Πρόλογος Μια άλλη προσέγγιση, όχι λιγότερο σημαντική για την κατανόηση, αναπτύσσεται στο Κεφάλαιο 9, αφιερωμένη στα τυχαία φράκταλ, ιδιαίτερα στην φράκταλ κίνηση Brown. Τέτοιες γενικεύσεις της κλασικής κίνησης Brown χρησιμοποιούνται ευρέως στη μοντελοποίηση φυσικών φαινομένων. Κατ 'αρχήν, το υλικό σε αυτό το κεφάλαιο μπορεί να διαβαστεί ανά πάσα στιγμή μετά το κεφάλαιο σχετικά με τις διαστάσεις. Το βιβλίο βασίζεται σε ένα μάθημα ενός εξαμήνου που δίδασκα στο Πανεπιστήμιο του Missouri-Columbia τα χρόνια. Οι ακροατές ήταν κυρίως μαθητές με ειδίκευση στα μαθηματικά, τις φυσικές επιστήμες, τις τεχνικές ειδικότητες και ορισμένους άλλους κλάδους. Τους πρότεινα να παρακολουθήσουν μαθήματα προχωρημένων στον λογισμό και τη γραμμική άλγεβρα πρώτα, αλλά γενικά αποδεκτούς ενδιαφερόμενους μαθητές που είχαν κάποια εμπειρία στη μαθηματική έρευνα, είτε καθαρά είτε εφαρμοσμένα μαθηματικά. Σε αντίθεση με την παραδοσιακή μορφή θεώρησης-απόδειξη-παράδειγμα-προβλήματος πολλών μαθηματικών μαθημάτων, η μοντελοποίηση υπολογιστή παίζει μεγάλο ρόλο στη μελέτη των φράκταλ και του χάους. Στην πραγματικότητα, οι περισσότεροι μαθητές μαθαίνουν πρώτα για την ύπαρξη φράκταλ βλέποντας εκπληκτικές εικόνες σε μια οθόνη υπολογιστή. Αυτό το βιβλίο προτείνει τη χρήση πειραμάτων υπολογιστή και θεωρίας μαζί, για τα οποία περιλαμβάνονται είκοσι αλγόριθμοι υπολογιστών. Αυτοί οι αλγόριθμοι δίνονται σε γενικευμένη μορφή, δηλαδή ανεξάρτητα από τη σύνταξη οποιασδήποτε συγκεκριμένης γλώσσας. Από την εμπειρία μου, δεν υπάρχει γλώσσα προγραμματισμού ή πακέτο λογισμικού που να ταιριάζει σε όλους. Οι μαθητές με τους οποίους αλληλεπίδρασα προγραμματίστηκαν σε Pascal, C, C++, Fortran, Matlab και Mathematica. Ένα από τα καλύτερα λογισμικά για πειραματισμούς με φράκταλ είναι το δωρεάν διαθέσιμο πρόγραμμα Fractint. Σας επιτρέπει να δημιουργήσετε μια ποικιλία φράκταλ και λειτουργεί εξαιρετικά γρήγορα. Μεγάλο μέρος του υλικού που είναι απαραίτητο για τη μελέτη των φράκταλ και του χάους περιλαμβάνεται στο κύριο κείμενο του βιβλίου. Καλύπτεται εν συντομία μια εισαγωγή στη θεωρία συνόλων, τους συγγενικούς μετασχηματισμούς, τους μετρικούς χώρους, τα σύνολα Cantor και τις καμπύλες Peano. Με εξαίρεση την ύλη του έβδομου κεφαλαίου, το βιβλίο περιέχει μόνο μερικές αποδείξεις που απαιτούν σοβαρή προετοιμασία σε επίπεδο προχωρημένου μαθήματος στον λογισμό. Τέτοια στοιχεία είναι σημαδεμένα

7 liptirutjiuaut - i με σημάδι (*). Μπορεί να παραλείπονται, αλλά συνιστάται στους μαθητές να απομνημονεύουν τις προτάσεις των θεωρημάτων. Άλλες, πιο σύνθετες παράγραφοι περιλαμβάνονται στο παράρτημα. Α. Ως αποτέλεσμα, το βιβλίο μπορεί να χρησιμοποιηθεί ως βάση για μαθήματα διαφορετικού βαθμού πολυπλοκότητας. Ένας λογαριασμός που εμμένει στα Κεφάλαια 1-6 και 8-9, δηλαδή εξαιρεί το Κεφάλαιο 7, "Χαοτική Δυναμική ΙΙ" και μετατρέπεται σε προσαρμ. Μόνο για λόγους αναφοράς, συνιστάται ως στοιχειώδες μάθημα. Σε διαφορετικά εξάμηνα κατάφερα να περάσω από μέρος του έβδομου κεφαλαίου και επιλεγμένες παραγράφους του παραρτήματος. Και, ειδικότερα, αφιερωμένο στη μέτρηση Hausdorff και στη διάσταση Hausdorff, αλλά μόνο με το κόστος της παράβλεψης ή της επιτάχυνσης της μελέτης μέρους του προηγούμενου υλικού. Οι ασπρόμαυρες εικόνες σε αυτό το βιβλίο εκτυπώνονται χρησιμοποιώντας το υποσύστημα γραφικών Postscript. Πολλές από τις εικόνες δημιουργήθηκαν στο Matlab, το οποίο είναι ιδιαίτερα χρήσιμο για την κατασκευή καμπυλών σε τρισδιάστατο χώρο. Το Matlab είναι επίσης κατάλληλο για προγραμματισμό και οπτικοποίηση συστημάτων L (Ενότητα 2.2), διαγραμμάτων αράχνης (Κεφάλαιο 6) και φράκταλ κίνησης Brownian (Κεφάλαιο 9). Εικόνες που απαιτούσαν πλήρωση περιοχών που οριοθετούνται από καμπύλες ελήφθησαν χρησιμοποιώντας το πακέτο Mathematica. Εικόνες που απαιτούσαν γραφικά bitmap (ένα δεδομένο pixel σε μια δεδομένη στιγμή για τον προσδιορισμό του χρώματός του, μαύρο ή άσπρο) δημιουργήθηκαν στο Fortran και στη συνέχεια μετατράπηκαν το αρχείο εξόδου σε μορφή Postscript. Με αυτόν τον τρόπο προέκυψε μια γραφική αναπαράσταση των συστημάτων επαναλαμβανόμενων συναρτήσεων από το τέταρτο κεφάλαιο και σύνθετης δυναμικής από το όγδοο κεφάλαιο. Τα έγχρωμα ένθετα έγιναν χρησιμοποιώντας το πρόγραμμα Practint. Θα ήθελα να εκφράσω τις ευχαριστίες μου για τη γόνιμη επικοινωνία στους συναδέλφους μου, οι οποίοι ενδιαφέρονται επίσης για τη θεωρία του χάους, τα φράκταλ και τα μαθηματικά που σχετίζονται με αυτές τις έννοιες. Καταρχάς, θα ήθελα να ευχαριστήσω τον J. Keller, ο οποίος με μύησε στα φράκταλ το 1984 όταν χρειαζόταν βοήθεια σε ένα ερευνητικό έργο φράκταλ, και τον μεταπτυχιακό του φοιτητή S. Chen, ο οποίος έχει αξιοσημείωτη γνώση του θέματος. Στη συνέχεια, έμαθα πολλά από ζωηρές συζητήσεις με τους K. Ahlbrandt, C. Chicone, D. Petty, P. Pfeiffer και P. Spekman. Είμαι ευγνώμων στον R. Delaware για τις σημειώσεις της διάλεξής του σχετικά με το θεώρημα του Sharkovsky, και στον P. Hagerty, ο οποίος ήταν μαθητής μου το 1993, για την επαγγελματική του βοήθεια στη δημιουργία των εικονογραφήσεων Mathematica.

8 8 Πρόλογος Ευχαριστώ πολύ τους E. Beltrami, A. C. Cliney, R. W. Easton και M. J. Field, R. D. Neidinger, A. Norton και K. Short, που έκαναν κριτική στο χειρόγραφο. Η μελετημένη κριτική και οι προτάσεις τους είχαν αναμφίβολα θετική επίδραση στην τελική έκδοση. Είμαι πολύ ευγνώμων στον C. Hesler, Jr., αντιπρόεδρο των Jones and Bartlett Publishers, για την ενεργητική βοήθειά του στην παραγωγή αυτού του εγχειριδίου. Ευχαριστώ πολύ τον P. Carroll και τον M. Cervantes των εκδόσεων Jones and Bartlett Publishers και τον M. Finley του Τμήματος Εκτυπώσεων, για τη δουλειά τους στην παραγωγή του βιβλίου. Θέλω ιδιαίτερα να ευχαριστήσω τη σύζυγό μου, Μαίρη, για την υπομονή και την υποστήριξή της καθ' όλη τη διάρκεια της συγγραφής αυτού του βιβλίου.

9 Κεφάλαιο 1. Εισαγωγή 1.1. Τι είναι τα φράκταλ και το χάος; Μια φορά κι έναν καιρό, στους περισσότερους ανθρώπους φαινόταν ότι η γεωμετρία στη φύση περιοριζόταν σε τόσο απλά σχήματα όπως η γραμμή, ο κύκλος, η κωνική τομή, το πολύγωνο, η σφαίρα, η τετραγωνική επιφάνεια και οι συνδυασμοί τους. Για παράδειγμα, τι θα μπορούσε να είναι πιο όμορφο από τη δήλωση ότι οι πλανήτες του ηλιακού μας συστήματος κινούνται γύρω από τον ήλιο σε ελλειπτικές τροχιές; Αυτός ο αξιοσημείωτος νόμος είναι ένα από τα τρία αξιώματα της κίνησης των πλανητών που διατυπώθηκαν από τον Johannes Kepler με βάση τις παρατηρήσεις και τις μετρήσεις που έγιναν από τον Tycho Brahe. Αργότερα, ο Sir Isaac Newton εξήγαγε τον νόμο του αντίστροφου τετραγώνου για τη βαρυτική έλξη ως λύση σε κάποια διαφορική εξίσωση, με τους νόμους του Kepler να ακολουθούν από τη λύση του. Σε αυτή και σε άλλες περιπτώσεις, όταν η εφαρμογή απλών γεωμετρικών μοντέλων ήταν επιτυχής, οδήγησε σε τεράστια επιστημονικά επιτεύγματα. Ωστόσο, πολλά φυσικά συστήματα είναι τόσο πολύπλοκα και ακανόνιστα που η χρήση μόνο οικείων αντικειμένων της κλασικής γεωμετρίας για τη μοντελοποίησή τους φαίνεται απελπιστική. Πώς, για παράδειγμα, μπορείτε να φτιάξετε ένα μοντέλο μιας οροσειράς ή μια κορώνα δέντρου από άποψη γεωμετρίας; Πώς να περιγράψετε την ποικιλομορφία των βιολογικών διαμορφώσεων που παρατηρούμε στον κόσμο των φυτών και των ζώων; Φανταστείτε την πολυπλοκότητα του κυκλοφορικού συστήματος, που αποτελείται από πολλά τριχοειδή αγγεία και αγγεία και παρέχει αίμα σε κάθε κύτταρο του ανθρώπινου σώματος. Φανταστείτε πόσο έξυπνα είναι διατεταγμένοι οι πνεύμονες και τα μπουμπούκια, που θυμίζουν στη δομή δέντρα με διακλαδισμένη κορώνα. Η δυναμική των πραγματικών φυσικών συστημάτων μπορεί να είναι εξίσου περίπλοκη και ακανόνιστη. Πώς να προσεγγίσετε τη μοντελοποίηση καταρρακτών ή ταραχωδών διεργασιών που καθορίζουν τον καιρό; Ποια μαθηματικά είναι υπεύθυνα για τους ρυθμούς της καρδιάς και του εγκεφάλου;

10 10 Κεφάλαιο 1 I Εισαγωγή Ο εγκέφαλος που παρατηρήθηκε στο ηλεκτροκαρδιογράφημα και το εγκεφαλογράφημα, ειδικά για εκείνες τις ξαφνικές κρίσεις αρρυθμίας που μπορεί να προκαλέσουν δυσλειτουργία της καρδιάς; Είναι δυνατόν να περιγραφεί μαθηματικά η ξαφνική εμφάνιση ενός κύματος πανικού στις χρηματοπιστωτικές αγορές ή ακόμη και να οικοδομηθεί ένα μαθηματικό μοντέλο κοινωνικής συμπεριφοράς; Τα φράκταλ και το μαθηματικό χάος είναι κατάλληλα μέσα για την εξερεύνηση των ερωτήσεων που τίθενται. Ο όρος φράκταλ αναφέρεται σε κάποια στατική γεωμετρική διαμόρφωση, όπως ένα στιγμιότυπο ενός καταρράκτη. Το χάος είναι ένας δυναμικός όρος που χρησιμοποιείται για να περιγράψει φαινόμενα παρόμοια με την ταραγμένη καιρική συμπεριφορά. Αυτό το βιβλίο είναι μια εισαγωγή στα μαθηματικά πίσω από αυτές τις έννοιες. Υποτίθεται ότι αφού κατακτήσει τις μεθόδους που περιγράφονται εδώ, ο αναγνώστης θα μπορεί να προχωρήσει στη μελέτη εφαρμογών από εξειδικευμένες πηγές 1. Για παράδειγμα, η έρευνα δείχνει ότι στη φυσιολογία υπάρχει και «καλό» χάος και «κακό» χάος. Σε πειράματα με γάτες, παρατηρήθηκε ότι η εμφάνιση του ηλεκτροκαρδιογραφήματος που λήφθηκε πριν και μετά τη χορήγηση κοκαΐνης αλλάζει από μια κανονική ακολουθία υψηλών κορυφών που ακολουθούνται από μικρές αιχμές σε μια εξαιρετικά ακανόνιστη αλληλουχία, πιθανώς υποδηλώνοντας επίθεση αρρυθμίας. Από την άλλη, το σχέδιο του ηλεκτροεγκεφαλογράμματος αλλάζει από ακανόνιστο και απρόβλεπτο σε πολύ πιο ομαλό. Δείτε επίσης την ανάλυση του πιθανού ρόλου του χάους στην ανάπτυξη καρδιοπαθειών. Συχνά αυτό που παρατηρούμε στη φύση μας ιντριγκάρει με την ατελείωτη επανάληψη του ίδιου μοτίβου, αυξημένο ή μειωμένο όσες φορές επιθυμούμε. Για παράδειγμα, ένα δέντρο έχει κλαδιά. Πάνω σε αυτά τα κλαδιά υπάρχουν μικρότερα κλαδιά κτλ. Θεωρητικά, το στοιχείο "διχάλα" επαναλαμβάνεται επ' αόριστον, γίνεται όλο και μικρότερο. Το ίδιο πράγμα μπορεί να δει κανείς όταν κοιτάζει μια φωτογραφία ορεινού εδάφους. Προσπαθήστε να κάνετε ζουμ λίγο στην οροσειρά και θα δείτε ξανά τα βουνά. Κάντε μεγαλύτερη μεγέθυνση και θα εξακολουθείτε να μπορείτε να βλέπετε τι μοιάζει με βουνά, χάρη στη (στατιστική) ικανότητά σας να διακρίνετε τον τύπο του αντικειμένου στην εικόνα. Έτσι εκδηλώνεται η ιδιότητα της αυτο-ομοιότητας που χαρακτηρίζει τα φράκταλ (Ενότητες 2.1 και 5.1). : Για περίεργους ελκυστήρες, χαοτική δυναμική και «δρόμους προς το χάος» βλ. Εδώ και παρακάτω υπάρχουν σημειώσεις υποσελίδων από μεταφραστές.

11 1.1 Τι είναι τα φράκταλ και το χάος; 11 Πολλές εργασίες για τα φράκταλ χρησιμοποιούν την αυτο-ομοιότητα ως καθοριστική ιδιότητα. Ακολουθώντας τον Benoit Mandelbrot, αποδεχόμαστε την άποψη ότι τα φράκταλ πρέπει να ορίζονται ως προς τη διάσταση του φράκταλ (Κεφάλαιο 5). Από εδώ προέρχεται η λέξη φράκταλ. Η έννοια της κλασματικής διάστασης είναι μια πολύ σύνθετη έννοια, την οποία θα παρουσιάσουμε σε διάφορα στάδια. Μια ευθεία γραμμή είναι ένα μονοδιάστατο αντικείμενο και ένα επίπεδο είναι δισδιάστατο. Όπως θα δούμε αργότερα, στρίβοντας καλά μια ευθεία γραμμή ή ένα επίπεδο, μπορείτε να αυξήσετε τη διάσταση της διαμόρφωσης που προκύπτει. Σε αυτήν την περίπτωση, η νέα διάσταση θα είναι συνήθως κλασματική κατά κάποια έννοια, την οποία πρέπει να διευκρινίσουμε. Η σύνδεση μεταξύ της κλασματικής διάστασης και της αυτο-ομοιότητας είναι ότι με τη βοήθεια της αυτο-ομοιότητας είναι δυνατό να κατασκευαστεί ένα σύνολο κλασματικών διαστάσεων με τον απλούστερο τρόπο (Ενότητα 2.1). Ακόμη και στην περίπτωση πολύ πιο πολύπλοκων φράκταλ, όπως το όριο του συνόλου Mandelbrot (Ενότητα 8.3), όταν δεν υπάρχει καθαρή αυτο-ομοιότητα, υπάρχει σχεδόν πλήρης επανάληψη της βασικής μορφής σε μια ολοένα και πιο μειωμένη μορφή. Στα αγγλικά, το χάος ορίζεται συνήθως ως μια κατάσταση πλήρους αταξίας ή σύγχυσης. Ορισμένα λεξικά χρησιμοποιούν την έννοια της κατάστασης στην οποία κυριαρχεί η τύχη. Ο όρος χάος στα μαθηματικά χρησιμοποιείται με στενή έννοια. Αν και δεν υπάρχει καθολικός ορισμός του μαθηματικού χάους, φαίνεται να υπάρχει πλήρης συμφωνία ότι κάθε είδους χάος έχει την ιδιότητα του απρόβλεπτου. Αυτή η ιδιότητα ονομάζεται ουσιαστική εξάρτηση από τις αρχικές συνθήκες (Ενότητα 6.5). Παραδόξως, δεν ισοδυναμεί με τυχαία συμπεριφορά. Στην πραγματικότητα, το μαθηματικό χάος είναι ένα χαρακτηριστικό γνώρισμα των ντετερμινιστικών δυναμικών συστημάτων. Επομένως, οι διακυμάνσεις που παρατηρούνται σε μια κατάσταση χάους φαίνονται μόνο τυχαίες· οι τιμές τους είναι εντελώς προκαθορισμένες από τις παραμέτρους εισόδου. Αλλά στην πράξη, δεν έχουμε ποτέ απολύτως ακριβείς πληροφορίες για τις αρχικές συνθήκες. Σφάλματα, ακόμα κι αν είναι ασήμαντα, συμβαίνουν πάντα κατά τη μέτρηση των παραμέτρων εισόδου. Αυτό που φαίνεται να είναι μια τυχαία έξοδος από ένα δυναμικό σύστημα οφείλεται σε μεγάλα σφάλματα που μπορεί να προκύψουν όταν το σύστημα συμπεριφέρεται χαοτικά. Κάποτε πίστευαν ότι σε ένα ντετερμινιστικό σύστημα, λαμβάνοντας υπόψη επαρκείς υπολογιστικούς πόρους, βρισκόμαστε πάντα μέσα

12 σε θέση να κάνει μια ουσιαστική πρόβλεψη (για παράδειγμα, να δώσει μια αξιόπιστη πρόγνωση καιρού), παρά τα μικρά λάθη στη μέτρηση της τρέχουσας κατάστασης. Στην παρουσία του χάους αυτό δεν συμβαίνει. Ακόμη και ο πιο ισχυρός υπολογιστής δεν θα μας επιτρέψει να κάνουμε μια ακριβή πρόβλεψη με βάση ένα μαθηματικό σύστημα με σημαντική εξάρτηση από τις αρχικές συνθήκες. Από την άποψή μας, το πιο ενδιαφέρον ερώτημα στη θεωρία των φράκταλ και του χάους είναι πώς να συνδέσουμε αυτές τις έννοιες μεταξύ τους. Πολλά σημαντικά φράκταλ, συμπεριλαμβανομένης της χιονονιφάδας Koch, του χαλιού Sierpinski και του κλασικού σετ Cantor που συζητήθηκε στο Κεφάλαιο 2, μπορούν να ληφθούν ως ελκυστήρες συστημάτων επαναλαμβανόμενων συναρτήσεων (Κεφάλαιο 4). Η ανάλυση αυτών των συστημάτων επαναλαμβανόμενων συναρτήσεων δείχνει τον δρόμο προς την κατασκευή χαοτικών τελεστών που σχετίζονται με τα αναφερθέντα φράκταλ (Κεφάλαιο 7). πριν αντιμετωπίστηκε με ατυχή εχθρότητα, καθώς Αυτό συνέβη στην ιστορία της ανάπτυξης πολλών άλλων μαθηματικών ιδεών. Ένας διάσημος μαθηματικός, ο Charles Hermite, τους ονόμασε ακόμη και τέρατα. Τουλάχιστον η γενική συναίνεση τα αναγνώριζε ως παθολογία που ενδιαφέρουν μόνο τους ερευνητές που καταχρώνται τις μαθηματικές μανίες και όχι τους πραγματικούς επιστήμονες. Ως αποτέλεσμα των προσπαθειών του Benoit Mandelbrot, αυτή η στάση άλλαξε και η γεωμετρία φράκταλ έγινε μια σεβαστή εφαρμοσμένη επιστήμη. Ο Mandelbrot επινόησε τον όρο fractal με βάση τη θεωρία του Hausdorff για την fractal (κλασματική) διάσταση, που προτάθηκε το 1919. Πολλά χρόνια πριν από την εμφάνιση του πρώτου του βιβλίου για τη γεωμετρία φράκταλ, ο Mandelbrot άρχισε να ερευνά την εμφάνιση τεράτων και άλλες παθολογίες στη φύση. Βρήκε μια θέση για τα ανυπόληπτα σετ Cantor, τις καμπύλες Peano, τις συναρτήσεις Weierstrass και τις πολλές παραλλαγές τους, που θεωρήθηκαν ανοησίες. Αυτός και οι μαθητές του ανακάλυψαν πολλά νέα φράκταλ, όπως φράκταλ Brownian κίνηση για μοντελοποίηση δασικών και ορεινών τοπίων, διακυμάνσεις της στάθμης του ποταμού και καρδιακούς παλμούς. Με τη δημοσίευσή του

13 1.2 Ιστορικό 13 βιβλίων οι εφαρμογές της φράκταλ γεωμετρίας άρχισαν να εμφανίζονται σαν μανιτάρια μετά τη βροχή. Αυτό επηρέασε τόσο πολλές εφαρμοσμένες επιστήμες όσο και καθαρά μαθηματικά. Ακόμη και η κινηματογραφική βιομηχανία δεν έμεινε απ' έξω. Εκατομμύρια άνθρωποι θαύμασαν το ορεινό τοπίο στην ταινία "Star Migration II: The Wrath of Khan", που κατασκευάστηκε με φράκταλ. Ο Γάλλος μαθηματικός Henri Poincaré ξεκίνησε την έρευνα στη μη γραμμική δυναμική γύρω στο 1890, οδηγώντας στη σύγχρονη θεωρία του χάους. Το ενδιαφέρον για το θέμα αυξήθηκε σημαντικά όταν ο Edward Lorenz, ένας μη γραμμικός μοντελιστής καιρού, ανακάλυψε το 1963 ότι οι μακροπρόθεσμες προβλέψεις καιρού ήταν αδύνατες. Ο Lorenz σημείωσε ότι ακόμη και μικρά λάθη στη μέτρηση της τρέχουσας κατάστασης των καιρικών συνθηκών μπορεί να οδηγήσουν σε εντελώς εσφαλμένες προβλέψεις για τις μελλοντικές καιρικές συνθήκες. Αυτή η ουσιαστική εξάρτηση από τις αρχικές συνθήκες βρίσκεται στη βάση της μαθηματικής θεωρίας του χάους. Οι τροχιές των σωματιδίων της Brownian κίνησης, οι οποίες μελετήθηκαν από τον Robert Brown ήδη από το 1828 και τον Albert Einstein το 1905, είναι ένα παράδειγμα φράκταλ καμπυλών, αν και η μαθηματική περιγραφή τους δεν δόθηκε μέχρι το 1923 από τον Norbert Wiener. Το 1890, ο Peano κατασκεύασε την περίφημη καμπύλη του, μια συνεχή χαρτογράφηση που μετατρέπει ένα τμήμα σε τετράγωνο και, ως εκ τούτου, αυξάνει τη διάστασή του από ένα σε δύο. Το όριο της νιφάδας χιονιού Koch (1904), του οποίου οι διαστάσεις είναι d και 1,2618, είναι μια άλλη γνωστή καμπύλη αύξησης των διαστάσεων. Ένα φράκταλ, σε καμία περίπτωση παρόμοιο με μια καμπύλη, που ο Mandelbrot ονόμασε σκόνη είναι το κλασικό σύνολο Cantor (1875 ή παλαιότερο). Αυτό το σετ είναι τόσο αραιό που δεν περιέχει διαστήματα, αλλά παρ' όλα αυτά έχει τον ίδιο αριθμό πόντων με το διάστημα. Ο Mandelbrot χρησιμοποίησε τέτοια «σκόνη» για να μοντελοποιήσει τον σταθερό θόρυβο στην τηλεφωνία. Η σκόνη φράκταλ του ενός ή του άλλου είδους εμφανίζεται σε πολλές περιπτώσεις. Στην πραγματικότητα, είναι ένα καθολικό φράκταλ με την έννοια ότι κάθε φράκταλ, ένας ελκυστήρας ενός συστήματος επαναλαμβανόμενων συναρτήσεων, είναι είτε φράκταλ σκόνη είτε η προβολή του σε χώρο χαμηλότερης διάστασης. Διάφορα φράκταλ που μοιάζουν με δέντρα χρησιμοποιήθηκαν όχι μόνο για τη μοντελοποίηση των δέντρων φυτών, αλλά και του βρογχικού δέντρου (κλαδιά που φέρουν αέρα στους πνεύμονες), της λειτουργίας των νεφρών και του κυκλοφορικού συστήματος.

14 14 Κεφάλαιο 1 / Εισαγωγή κ.λπ. Είναι ενδιαφέρον να σημειωθεί η υπόθεση του Leonardo da Vinci ότι όλα τα κλαδιά ενός δέντρου σε ένα δεδομένο ύψος, όταν αθροίζονται μαζί, είναι ίσα σε πάχος με τον κορμό (κάτω από το επίπεδό τους). Αυτό συνεπάγεται ένα φράκταλ μοντέλο για το στέμμα του δέντρου με τη μορφή φράκταλ επιφάνειας. Πολλές αξιοσημείωτες ιδιότητες των φράκταλ και του χάους αποκαλύπτονται με τη μελέτη επαναλαμβανόμενων χαρτογραφήσεων. Στην περίπτωση αυτή ξεκινούν με κάποια συνάρτηση y = f(x) και εξετάζουν τη συμπεριφορά της ακολουθίας /(x), /(/(x)), /(/(/(x))),... Σε το σύνθετο επίπεδο, έργο αυτού του είδους ανεβαίνει, προφανώς, στο όνομα του Cayley, ο οποίος ερεύνησε τη μέθοδο του Νεύτωνα για την εύρεση της ρίζας όπως εφαρμόζεται σε σύνθετες, και όχι μόνο πραγματικές, συναρτήσεις (1879). Αξιοσημείωτη πρόοδος στη μελέτη των επαναλαμβανόμενων σύνθετων χαρτογραφήσεων έγινε από τους Gaston Julia και Pierre Fatou (1919). Φυσικά, όλα έγιναν χωρίς τη βοήθεια γραφικών υπολογιστή. Αυτές τις μέρες, πολλοί έχουν ήδη δει πολύχρωμες αφίσες που απεικονίζουν σκηνικά της Τζούλια και το σετ Mandelbrot, που σχετίζεται στενά με αυτά. Είναι φυσικό να αρχίσουμε να κυριαρχούμε στη μαθηματική θεωρία του χάους με επαναλαμβανόμενες χαρτογραφήσεις. Η μελέτη των φράκταλ και του χάους ανοίγει υπέροχες δυνατότητες, τόσο στη μελέτη ενός άπειρου αριθμού εφαρμογών όσο και στον τομέα των καθαρών μαθηματικών. Ταυτόχρονα όμως, όπως συμβαίνει συχνά στα λεγόμενα νέα μαθηματικά, οι ανακαλύψεις βασίζονται στο πρωτοποριακό έργο των μεγάλων μαθηματικών του παρελθόντος. Ο Sir Isaac Newton το κατάλαβε όταν είπε: «Αν έχω δει πιο μακριά από άλλους, είναι επειδή έχω σταθεί στους ώμους γιγάντων».

15 Κεφάλαιο 2. Κλασικά φράκταλ 2.1. Αυτο-ομοιότητα Ας διαιρέσουμε ένα ευθύγραμμο τμήμα σε Ν ίσα μέρη. Στη συνέχεια, κάθε τμήμα μπορεί να θεωρηθεί αντίγραφο ολόκληρου του τμήματος, μειωμένο κατά 1/r φορές. Προφανώς, τα N και r σχετίζονται με τη σχέση Nr = 1 (Εικ. 2.1). Εάν το τετράγωνο χωριστεί σε Ν ίσα τετράγωνα (με εμβαδόν 1/g 2 φορές μικρότερο από το εμβαδόν του αρχικού), τότε η αναλογία θα γραφεί ως Nr 2 = 1. Εάν ο κύβος χωριστεί σε Ν ίσους κύβους (με όγκο 1/g 3 φορές μικρότερο από τον αρχικό όγκο), τότε η σχέση θα έχει την ακόλουθη μορφή: iw 3 = 1. Σημειώστε ότι η διάσταση d ενός αντικειμένου, είτε πρόκειται για μονοδιάστατο τμήμα, είτε για δύο διαστάσεων τετράγωνο ή τρισδιάστατος κύβος, εμφανίζεται ως δύναμη r στη σχέση μεταξύ JV, του αριθμού ίσων υποαντικειμένων και του συντελεστή ομοιότητας r. Δηλαδή: Nr d = 1. (2.1) Τα σύνολα που κατασκευάζονται στο Σχ. 2.1, έχουν διάσταση ακέραιου αριθμού. Ας αναρωτηθούμε εάν είναι δυνατή μια τέτοια κατασκευή στην οποία ο εκθέτης d στην ισότητα (2.1) δεν είναι ακέραιος, δηλαδή, έτσι ώστε όταν το αρχικό σύνολο διαιρείται σε Ν ασύνδετα υποσύνολα που λαμβάνονται με την κλιμάκωση του πρωτοτύπου με έναν παράγοντα r, η τιμή του d δεν θα εκφραστεί ως ακέραιος αριθμός. Η απάντηση, όπως θα δούμε, είναι ένα ηχηρό ναι! Ένα τέτοιο σύνολο ονομάζεται αυτο-όμοιο φράκταλ. Η τιμή d ονομάζεται φράκταλ (κλασματική) διάσταση ή διάσταση ομοιότητας. Μια ρητή έκφραση για το d ως προς το N και το r βρίσκεται λαμβάνοντας τον λογάριθμο και των δύο πλευρών του (2.1): Ο λογάριθμος μπορεί να ληφθεί σε οποιαδήποτε θετική βάση εκτός από τη μονάδα, για παράδειγμα στη βάση 10 ή στη βάση e «2,

16 16 Κεφάλαιο 2 / Κλασικά φράκταλ e o o o N=3 r=1/3 d=l N=9t=l/3d=2 / N=27 g=sq d=3 Σχ. Σχέση διάστασης και συντελεστή ομοιότητας Ένας γενικότερος τύπος Self -παρόμοια φράκταλ συζητούνται στη σ. Ένα φράκταλ μπορεί ακόμα να είναι μια ένωση ασύνδετων υποσυνόλων που λαμβάνονται με την κλιμάκωση του αρχικού, αλλά οι συντελεστές ομοιότητας δεν είναι πλέον απαραίτητα οι ίδιοι για όλα τα υποσύνολα. Σε αυτήν την περίπτωση, ο τύπος για τη διάσταση (2.2) δεν ισχύει. Ο όρος φράκταλ εισήχθη για πρώτη φορά το 1975 από τον Benoit Mandelbrot, έναν πρωτοπόρο στον τομέα της γεωμετρίας φράκταλ.1 Πολλές μαθηματικές ιδέες διαμορφώθηκαν πολύ πριν από αυτό, τον 19ο αιώνα, στα έργα των Georg Cantor, Karl Weierstrass, Giuseppe Peano και οι υπολοιποι. Η έννοια της φράκταλ (κλασματικής) διάστασης εμφανίστηκε το 1919 στο έργο του Felix Hausdorff. Ωστόσο, ήταν ο Mandelbrot που συγκέντρωσε αυτές τις ιδέες και ξεκίνησε τη συστηματική μελέτη των φράκταλ και των εφαρμογών τους. Στο 5ο κεφάλαιο και παράρτημα. Α.5 θα δοθεί μια αυστηρή μαθηματική παρουσίαση θεμάτων που σχετίζονται με την κλασματική διάσταση. Επιπλέον, ο όρος fractal προέρχεται από το λατινικό ρήμα frangere to break και το επίθετο fractus fractional.

17 2.1 Αυτο-ομοιότητα 17 Fig Koch's Snowflake Θα πρέπει να έχουμε κατά νου ότι η έννοια του φράκταλ βρίσκεται ακόμη σε εξέλιξη και διαφορετικές πηγές μπορεί να χρησιμοποιούν διαφορετικούς ορισμούς. Σημειώστε εδώ ότι ορισμένα σύνολα ακέραιων διαστάσεων είναι επίσης φράκταλ, όπως προκύπτει από τον ορισμό μας. Νιφάδα χιονιού Κοχ. Το όριο μιας νιφάδας χιονιού, που εφευρέθηκε από τον Helg von Koch το 1904 (Εικ. 2.2), περιγράφεται από μια καμπύλη που αποτελείται από τρία πανομοιότυπα φράκταλ με διάσταση d "1,2618. Κάθε τρίτο της νιφάδας χιονιού κατασκευάζεται επαναληπτικά, ξεκινώντας από τη μία πλευρά του ισόπλευρου τριγώνου. Έστω KQ το αρχικό τμήμα. Ας αφαιρέσουμε το μεσαίο τρίτο και ας προσθέσουμε δύο νέα τμήματα του ίδιου μήκους, όπως φαίνεται στο Σχ. Ας ονομάσουμε το σύνολο που προκύπτει K\. Ας επαναλάβουμε αυτή τη διαδικασία πολλές φορές, σε κάθε βήμα αντικαθιστώντας το μεσαίο τρίτο με δύο νέα τμήματα. Ας συμβολίσουμε με Kn το σχήμα που προκύπτει μετά το nο βήμα. Είναι διαισθητικά σαφές ότι η ακολουθία των καμπυλών (K n )^=i συγκλίνει σε κάποια οριακή καμπύλη K. Θα διεξάγουμε μια αυστηρή μαθηματική μελέτη της σύγκλισης τέτοιων ακολουθιών καμπυλών και άλλων συνόλων στην Ενότητα 3.5 και στην Εφαρμογή. Ο Α.Ζ. Προς το παρόν, ας υποθέσουμε ότι η καμπύλη K υπάρχει και ας εξετάσουμε μερικές από τις ιδιότητές της.

18 18 Κεφάλαιο 2 / Κλασικά φράκταλ (α) (β) (γ) (δ) Σχήμα α) Κο, β) Κ και γ) Κ 2, δ) Κ 3, Αν πάρετε ένα αντίγραφο του Κ, μειωμένο κατά τρεις φορές (g = 1/3), τότε ολόκληρο το σύνολο K μπορεί να αποτελείται από N = 4 τέτοια αντίγραφα. Συνεπώς, η σχέση αυτο-ομοιότητας (2.1) ικανοποιείται για τα υποδεικνυόμενα LG και r και η διάσταση του φράκταλ θα είναι:

19 2.1 VaMonododue 1U Fig Sierpinski Carpet Θεώρημα Το όριο μιας νιφάδας χιονιού Koch έχει άπειρο μήκος. Απόδειξη. Αρκεί να δείξουμε ότι καθένα από τα τρία πανομοιότυπα φράκταλ K που λαμβάνονται με επαναλήψεις (Εικ. 2.3) έχει άπειρο μήκος. Αφήστε το αρχικό τμήμα να έχει μήκος μονάδας. Τότε το μήκος της καμπύλης K\ είναι 4/3. Το μήκος της καμπύλης K2 είναι 4 2 /3 2. Συνεχίζοντας έτσι, έχουμε ότι η καμπύλη K n μετά το nο βήμα έχει μήκος 4 "/3". Κατά συνέπεια, το μήκος της οριακής καμπύλης Κ είναι ίσο με το άπειρο: λίρες 4 n /3 n = 00. Χαλί Sierpinski. Ένα άλλο παράδειγμα απλού αυτο-όμοιου φράκταλ είναι το χαλί Sierpinski (Εικ. 2.4), που εφευρέθηκε από τον Πολωνό μαθηματικό Waclaw Sierpinski το 1915. Ο ίδιος ο όρος χαλί (φλάντζα) ανήκει στον Mandelbrot. Στην παρακάτω μέθοδο κατασκευής, ξεκινάμε με μια συγκεκριμένη περιοχή και εξαλείφουμε διαδοχικά τις εσωτερικές υποπεριοχές. Αργότερα θα εξετάσουμε άλλες μεθόδους, ιδιαίτερα χρησιμοποιώντας συστήματα L (Ενότητα 2.2), καθώς και βασισμένες σε συστήματα επαναλαμβανόμενων συναρτήσεων (Κεφάλαιο 4). Έστω το αρχικό σύνολο SQ ένα ισόπλευρο τρίγωνο μαζί με την περιοχή που περικλείει. Ας χωρίσουμε το SQ στα τέσσερα

20 20 Κεφάλαιο 2 / Κλασικά φράκταλ Εικ. Κατασκευή χαλιού Sierpinski μικρότερες τριγωνικές επιφάνειες συνδέοντας τα μέσα των πλευρών του αρχικού τριγώνου με τμήματα. Ας αφαιρέσουμε το εσωτερικό της μικρής κεντρικής τριγωνικής περιοχής. Ας ονομάσουμε το υπόλοιπο σύνολο S\ (Εικ. 2.5). Στη συνέχεια επαναλαμβάνουμε τη διαδικασία για καθένα από τα τρία εναπομείναντα μικρά τρίγωνα και λαμβάνουμε την ακόλουθη προσέγγιση 5d. Συνεχίζοντας με αυτόν τον τρόπο, λαμβάνουμε μια ακολουθία ένθετων συνόλων S n, των οποίων η τομή σχηματίζει το χαλί 5. Από την κατασκευή είναι ξεκάθαρο ότι ολόκληρο το χαλί είναι μια ένωση N 3 ουσιαστικά ασύνδετων αντιγράφων που έχουν μειωθεί στο μισό. συντελεστής ομοιότητας r = 1/2 (τόσο οριζόντια όσο και κάθετα). Επομένως, το 5 είναι ένα αυτο-όμοιο φράκταλ με διάσταση: d = log(3)/log(2) “1,5850. Προφανώς, το συνολικό εμβαδόν των εξαρτημάτων που πετάγονται κατά την κατασκευή είναι ακριβώς ίσο με το εμβαδόν του αρχικού τριγώνου. Στο πρώτο βήμα πετάξαμε το 1/4 της περιοχής. Στο επόμενο βήμα, πετάξαμε τρία τρίγωνα, το καθένα με εμβαδόν ίσο με το 1/4 2 του εμβαδού του αρχικού. Συλλογιζόμενοι κατ' αυτόν τον τρόπο, είμαστε πεπεισμένοι ότι το συνολικό μερίδιο της απορριφθείσας έκτασης ήταν: 1/4 + 3(1/4 2) (1/4 3) + + 3 + Το ποσό αυτό είναι ίσο με 1 (Π.χ. 4 στο το τέλος αυτής της ενότητας). Επομένως, μπορούμε να ισχυριστούμε ότι το υπόλοιπο σύνολο S, δηλαδή το χαλί,

21 2.2 Αυτο-ομοιότητα Το 21 έχει εμβαδόν μέτρου μηδέν. Αυτό κάνει το S ένα «τέλειο» σύνολο, με την έννοια ότι χωρίζει το συμπλήρωμά του σε άπειρο αριθμό τριγωνικών περιοχών, ενώ έχει μηδενικό πάχος. σφουγγάρι του Menger. Υπάρχουν επίσης τρισδιάστατα ανάλογα χαλιών. Ακολουθώντας τον Mandelbrot, τέτοια σύνολα ονομάζουμε σφουγγάρια. Το σφουγγάρι που φαίνεται στο Σχ. 2.6, ονομάζεται σφουγγάρι Menger, που πήρε το όνομά του από τον Carl Menger. Αυτό είναι ένα αυτο-όμοιο φράκταλ με N = 20 και r = 1/3. Η διάστασή του είναι: d = log(20)/ log(3) * 2,7268. Ένα τέτοιο σφουγγάρι έχει όγκο μέτρου μηδέν. Αφήνουμε τις λεπτομέρειες κατασκευής και ανάλυσης στον αναγνώστη. Ασκήσεις Προσδιορίστε την κλασματική διάσταση (διάσταση ομοιότητας) των φράκταλ που κατασκευάζονται όπως φαίνεται στο Σχ. Προσδιορίστε την κλασματική διάσταση (διάσταση ομοιότητας) των φράκταλ που κατασκευάζονται όπως φαίνεται στο Σχ. Κατασκευάστε ένα φράκταλ διαφορετικό από το φράκταλ στο Σχ. 2.8(α), αλλά της ίδιας διάστασης. 4. Δείξτε ότι το άθροισμα των εμβαδών των τριγώνων που απορρίφθηκαν κατά την κατασκευή του χαλιού Sierpinski είναι ίσο με το εμβαδόν του αρχικού τριγώνου. Υπόδειξη: χρησιμοποιήστε τη σχέση: 1/(1 - x) = 1 + x + x 2 -\, για x< Рассмотрим фрактал, который строится, как указано на рис Этот фрактал иногда называют пылью Серпинского. Записать бесконечный ряд для суммы площадей частей, которые были удалены при построении. Найти сумму этого ряда. 6. (Компьютерный эксперимент.) Исследовать, какая связь существует между треугольником Паскаля (состоящим из биномиальных коэффициентов) и ковром Серпинского(см. ).

22 22 Κεφάλαιο 2 / Κλασικά φράκταλ Εικ. Κατασκευή του σφουγγαριού Menger (α) (β) 1 c -HI o 1, c 1 (γ) (δ) Εικ. Κατασκευές για άσκηση. 1

23 2.2 Συστήματα L 23 (α) (β) Εικ. Κατασκευές για άσκηση. 2 Εικ. Κατασκευές για τον έλεγχο των L-συστημάτων Η έννοια των L-συστημάτων, στενά συνδεδεμένη με αυτοπαρόμοια φράκταλ, εμφανίστηκε μόλις το 1968 χάρη στον Aristrid Lindenmayer. Τα συστήματα L εισήχθησαν αρχικά στη μελέτη των επίσημων γλωσσών και χρησιμοποιήθηκαν επίσης σε βιολογικά μοντέλα επιλογής. Μπορούν να χρησιμοποιηθούν για την κατασκευή πολλών γνωστών αυτο-παρόμοιων φράκταλ, συμπεριλαμβανομένης της νιφάδας χιονιού Koch και του χαλιού Sierpinski. Κάποιες άλλες κλασικές κατασκευές, για παράδειγμα οι καμπύλες Peano (έργα των Peano, Hilbert, Sierpinski), ταιριάζουν επίσης σε αυτό το σχήμα. Και φυσικά, τα συστήματα L ανοίγουν το δρόμο σε μια άπειρη ποικιλία νέων φράκταλ, κάτι που ήταν ο λόγος για την ευρεία χρήση τους στα γραφικά υπολογιστών για την κατασκευή φράκταλ δέντρων και φυτών. Ακολουθεί η παρουσίασή μας των συστημάτων L

24 24 Κεφάλαιο 2 / Κλασικά φράκταλ κυρίως στο έργο των Pruzinkevich και Hanan και περιορίζεται στην περίπτωση των ντετερμινιστικών συστημάτων L και των επίπεδων γραφικών. Για τη γραφική υλοποίηση συστημάτων L, τα λεγόμενα τριτογενή γραφικά (turtle turtle) χρησιμοποιούνται ως υποσύστημα εξόδου. Σε αυτή την περίπτωση, η κουκκίδα (χελώνα) κινείται κατά μήκος της οθόνης σε διακριτά βήματα, συνήθως ιχνηλατώντας το σημάδι της, αλλά εάν είναι απαραίτητο μπορεί να κινηθεί χωρίς σχέδιο. Έχουμε τρεις παραμέτρους στη διάθεσή μας (x, y, a), όπου (x, y) είναι οι συντεταγμένες της χελώνας και η κατεύθυνση προς την οποία κοιτάζει. Η χελώνα εκπαιδεύεται να ερμηνεύει και να εκτελεί μια ακολουθία εντολών που δίνονται από μια κωδική λέξη, τα γράμματα της οποίας διαβάζονται από αριστερά προς τα δεξιά. Η κωδική λέξη είναι το αποτέλεσμα του συστήματος L και μπορεί να περιλαμβάνει τα ακόλουθα γράμματα: F προχωρήστε ένα βήμα μπροστά, σχεδιάζοντας ένα ίχνος. β προχωρήστε ένα βήμα μπροστά χωρίς να τραβήξετε ίχνος. [ άνοιγμα κλάδου (δείτε παρακάτω για λεπτομέρειες) ] κλείσιμο κλάδου (δείτε παρακάτω για λεπτομέρειες) + αύξηση γωνίας a κατά ποσό b μείωση γωνίας a κατά ποσό b Το μέγεθος βήματος και η τιμή αύξησης κατά μήκος της γωνίας b έχουν οριστεί εκ των προτέρων και παραμένουν αμετάβλητα για όλες οι κινήσεις της χελώνας. Εάν η αρχική κατεύθυνση της κίνησης a (η γωνία που μετράται από τη θετική κατεύθυνση του άξονα Χ) δεν είναι καθορισμένη, τότε ορίζουμε ένα ίσο με το μηδέν. Πολλά παραδείγματα επεξηγούν τη χρήση εντολών διακλάδωσης (που συμβολίζονται με ], [) και βοηθητικών μεταβλητών (που συμβολίζονται με Χ, Υ, κ.λπ.). Οι εντολές διακλάδωσης χρησιμοποιούνται για την κατασκευή δέντρων και φυτών και οι βοηθητικές μεταβλητές κάνουν την κατασκευή ορισμένων συστημάτων L πολύ πιο εύκολη. Τυπικά, ένα ντετερμινιστικό σύστημα L αποτελείται από ένα αλφάβητο, μια λέξη αρχικοποίησης που ονομάζεται αξίωμα ή εκκινητή, και ένα σύνολο γενεσιουργών κανόνων που υποδεικνύουν πώς πρέπει να μετασχηματιστεί η λέξη καθώς μετακινείται από επίπεδο σε επίπεδο (επανάληψη σε επανάληψη). Για παράδειγμα, μπορεί κανείς να αντικαταστήσει το γράμμα F χρησιμοποιώντας τον γενετικό κανόνα newf = F F+-f-F F, που αντιστοιχεί στο σύστημα L για τη νιφάδα χιονιού Koch που συζητείται παρακάτω. Τα σύμβολα +, ], [ δεν ενημερώνονται, αλλά απλώς παραμένουν στα σημεία όπου εμφανίζονται. Η ενημέρωση των γραμμάτων σε μια δεδομένη λέξη θεωρείται ότι είναι ταυτόχρονη,

25 2.2 Συστήματα L 25 δηλαδή, όλα τα γράμματα μιας λέξης σε ένα επίπεδο ενημερώνονται πριν από οποιοδήποτε γράμμα στο επόμενο επίπεδο. Το σύστημα L που αντιστοιχεί στη νιφάδα χιονιού Koch (Εικ. 2.2) ορίζεται ως εξής: 0 = m/3 Αξίωμα: F++F++F Κανόνας δημιουργίας: newf = F F++F F Γραφική αναπαράσταση του αξιώματος F+ +F++ Το F είναι ισόπλευρο τρίγωνο. Η χελώνα κάνει ένα βήμα μπροστά, στη συνέχεια η γωνία α αυξάνεται κατά 2 tg/3 και η χελώνα κάνει άλλο ένα βήμα προς τα εμπρός, η γωνία α αυξάνεται ξανά κατά 2 tg/3 και η χελώνα κάνει άλλο ένα βήμα. Στο πρώτο βήμα, κάθε γράμμα F στην αρχική λέξη F++F++F αντικαθίσταται από F-F++F F: (F-F++F-F)++(F-F++F-F)++( F-F ++F-F). Αφαιρώντας τις αγκύλες, παίρνουμε: F-F++F-F++F-F++F-F++F-F++F-F. Επαναλαμβάνοντας αυτή τη διαδικασία, στο δεύτερο βήμα παίρνουμε: F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F++ F-F++F-F-F-F++F-F ++F-F++F-F-F-F++F-F++ F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F κ.λπ. Κανόνες ψευδοκώδικα για επανάληψη γεννητριών σε αυτό Η απλούστερη περίπτωση, όταν χρησιμοποιούνται μόνο κανόνες της μορφής F = newf, b = newb, μοιάζει με αυτό: Αλγόριθμος (L-SYSTEM) Σκοπός: υλοποιεί τους κανόνες F = newf, b = newb. Είσοδος: αξίωμα (λέξη αρχικοποίησης) newf (κανόνας δημιουργίας) newb (κανόνας δημιουργίας) επίπεδο (αριθμός επαναλήψεων) Έξοδος: λέξη (λέξη αποτελέσματος)

26 26 Κεφάλαιο 2 / Κλασικά φράκταλ Αρχικοποίηση: W = αξίωμα n = μήκος(w) Т = ( ) (κενό σύνολο) Βήματα: ενώ επίπεδο > 0 για j = 1 έως n αν W(j) = +,T = (T +), τέλος αν i W(j) = -,T = (T -), τέλος αν αν W(j) = [,T = (T [), τέλος αν ii-w(j) = ],T = (T ]), τέλος εάν αν W(j) = F,T = (T newf), τέλος εάν αν W(j) = b,t = (T τέλος για W = T επίπεδο = επίπεδο 1 τέλος ενώ λέξη = W newb), τέλος αν Σημείωση: W(j) είναι το j-ο γράμμα της λέξης W, (T που έχει συνδεδεμένο σύμβολο +. +) συμβολοσειρά T, σε Θα δούμε αργότερα τον αντίστοιχο ψευδοκώδικα για τα γραφικά της χελώνας σε ΑΥΤΗΝ την ΕΝΟΤΗΤΑ. Μια λίστα κανόνων δημιουργίας για τα διάφορα συστήματα L που αναφέρονται στο κείμενο μπορείτε να βρείτε στο τέλος αυτής της ενότητας. Το γράφημα στο Σχ. δεν έχει σπασίματα, αφού η χελώνα κινείται σε μεμονωμένα βήματα και χαράζει το δικό της ίχνος κάθε φορά. Τα ασυνεχή γραφήματα μπορούν να ληφθούν χρησιμοποιώντας την εντολή «b» στο σύστημα L, δηλαδή την εντολή «προχωρήστε ένα βήμα μπροστά χωρίς να σχεδιάσετε». Τα παραδείγματα περιλαμβάνουν εικόνες ψηφιδωτών στο Σχ. και αλυσίδες στο Σχ. Κατά την κατασκευή φράκταλ χρησιμοποιώντας μόνο έναν κανόνα παραγωγής, προκύπτει η ακόλουθη δυσκολία. Δεν μπορούμε να αλλάξουμε την κατεύθυνση ανάγνωσης του κανόνα σε κάποια βήματα, δηλαδή να τον διαβάσουμε όχι από αριστερά προς τα δεξιά, αλλά από δεξιά προς τα αριστερά. Χωρίς να λυθεί αυτό το πρόβλημα, είναι αδύνατο να ληφθούν συστήματα L για καμπύλες Peano, τα οποία συζητούνται στην επόμενη ενότητα.

27 2.2 Συστήματα L 27 Εικ. Νησί μετά από 2 επαναλήψεις Για παράδειγμα, για να κατασκευαστεί ένα φράκταλ που ονομάζεται «δράκος του δρόμου Harter-Highway», είναι απαραίτητο να μπορείτε να αλλάξετε την κατεύθυνση ανάγνωσης του κανόνα παραγωγής που φαίνεται στο Σχ. Α. Η καμπύλη χρησιμοποιείται ως εκκινητής ή αξίωμα αριστερά. Ο κανόνας παραγωγής σε αυτή την περίπτωση είναι να τραβήξετε τον εκκινητή πρώτα προς την εμπρός κατεύθυνση και μετά προς την αντίστροφη κατεύθυνση. Ένα τέτοιο σχήμα δεν εντάσσεται στο πλαίσιο των συστημάτων L που χρησιμοποιούν μόνο έναν κανόνα παραγωγής. Αυτό το πρόβλημα μπορεί να λυθεί εισάγοντας δύο διαφορετικές εντολές για να προχωρήσουμε μπροστά, για παράδειγμα X και Y. Θα υποθέσουμε ότι η χελώνα ερμηνεύει τα X και Y με τον ίδιο τρόπο, δηλαδή ως ένα βήμα μπροστά. Χρησιμοποιώντας αυτά τα δύο γράμματα, ο γενεσιουργός κανόνας για τον δράκο μπορεί να γραφτεί ως εξής: αξίωμα = X, newx = X+Y+, newy = X-Y. Ωστόσο, δεν θα θέλαμε να εγκαταλείψουμε την αρχική προσέγγιση, στην οποία ερμηνεύεται μόνο ένα γράμμα F

28 28 Κεφάλαιο 2 / Κλασικά Fractals Fig Μωσαϊκό μετά από 3 επαναλήψεις (Patrick Hagerty) Μπορεί να γίνει ένα βήμα μπροστά. Για να επιστρέψουμε στο πλαίσιο αυτής της προσέγγισης, θα θεωρήσουμε τα γράμματα X και Y ως βοηθητικές μεταβλητές που αγνοούνται από τη χελώνα και θα τα αντικαταστήσουμε στον κανόνα παραγωγής με FX και FY, αντίστοιχα. Παίρνουμε: αξίωμα = FX, FX = FX+YF+, YF = -FX-YF. Σημειώνουμε περαιτέρω ότι το ίδιο αποτέλεσμα μπορεί να επιτευχθεί χρησιμοποιώντας τους ακόλουθους κανόνες δημιουργίας: αξίωμα = FX, newf = F, newx = X+YF+, newy = -FX-Y.

29 2.2 Συστήματα L 29 Εικ. Αλυσίδα μετά από 3 επαναλήψεις (Yan-Xi Lo) * Κανόνας δημιουργίας 3 εκκινητή Εικ. Εκκινητής και κανόνας για τον δράκο Harter-Highway

30 30 Κεφάλαιο 2 j Κλασικά Fractals Σχήμα Harter-Highway Dragon μετά από 12 επαναλήψεις Ακολουθούν διάφορα βήματα για την κατασκευή ενός δράκου χρησιμοποιώντας αυτούς τους γενετικούς κανόνες: 1ο βήμα: FX+YF+ 2ο βήμα: FX+YF++-FX-YF+ 3 1ο βήμα: FX+ YF++-FX-YF++-FX+YF+ FX-YF+ 4ο βήμα: FX+YF++-FX-YF++-FX+YF+ FX-YF++ -FX+YF++-FX-YF+ FX+YF+ FX- YF+ Το σχήμα δείχνει έναν δράκο μετά το 12 επαναλήψεις. Σημειώστε ότι ο δράκος αποτελείται από πολλά παρόμοια μέρη. Εν κατακλείδι, ας δούμε τη λειτουργία διακλάδωσης. Όταν συναντάμε το σύμβολο [ (ανοιχτός κλάδος), θυμόμαστε τη θέση και την κατεύθυνση της χελώνας, δηλαδή τις μεταβλητές (x, y, a) και επιστρέφουμε σε αυτές τις ρυθμίσεις αργότερα. Για αποθήκευση τριδύμων (x, y, a)

31 2.% L-system Fig Weed μετά από 4 επαναλήψεις η στοίβα "x\ yx ah X2 Y2 "2 X n Up "n χρησιμοποιείται και νέα δεδομένα γράφονται στο τέλος της στοίβας. Όταν ο κλάδος είναι κλειστός, στις μεταβλητές (x, y, a) εκχωρούνται οι τιμές που διαβάζονται από το τέλος της στοίβας. Αυτές οι τιμές στη συνέχεια αφαιρούνται από τη στοίβα. Έτσι, ένας κλάδος καθορίζεται με δύο σύμβολα: [ Άνοιγμα κλάδου. Αποθηκεύστε (zh, y, a) στο τέλος της στοίβας. ] Κλείστε το υποκατάστημα. Αντιστοιχίστε στις μεταβλητές (x, y, a) τις τιμές που διαβάζονται από το τέλος της στοίβας και, στη συνέχεια, αφαιρέστε τις από τη στοίβα. Το σχήμα και το 2.16 δείχνουν φράκταλ που κατασκευάστηκαν χρησιμοποιώντας τη λειτουργία διακλάδωσης. Παρακάτω είναι ένας αλγόριθμος που σας επιτρέπει να αποκτήσετε μια γραφική αναπαράσταση μιας λέξης χρησιμοποιώντας γραφικά χελώνας.

32 32 Κεφάλαιο 2 / Αλγόριθμος κλασικών φράκταλ (ΓΡΑΦΙΚΑ ΧΕΛΩΝΩΝ) Σκοπός: υλοποιεί γραφικά χελώνας για κωδική λέξη που αποτελείται από τα γράμματα F, b, [, ], + και. Είσοδος: λέξη (αποτέλεσμα του συστήματος L) σε (αύξηση γωνίας) α (αρχική κατεύθυνση) Έξοδος: Γραφική αναπαράσταση λέξης. Αρχικοποίηση: γραφική λειτουργία (δείτε παρακάτω για λεπτομέρειες) W = λέξη n = \ength(λέξη) στοίβα = ( ) (κενό σύνολο) Βήματα: για j = 1 έως n εάν W(j) = +, o = a + γ, τέλος αν αν W(j) -, a = a 9, τέλος αν αν W(j) = F, x = x 0 + cos(o;), y = yo + sin(a), σχεδιάστε μια γραμμή από το σημείο (ho ,уо) στο σημείο (x, y), x 0 = x, Uo = U τέλος αν W(j) = 6, XQ = XQ + cos(a), j/o = Уо + sin( α), τέλος εάν / = μήκος (στοίβα), στοίβα (I + 1,1) = στοίβα XQ (I + 1,2) = στοίβα yo (I + 1,3) = ένα τέλος αν W(j) = ], I = μήκος (στοίβα), XQ = στοίβα (/, 1) 2/o = στοίβα (1,2) μια στοίβα (/,3)

33 2.2 L-systems 33 Εικ. Bush μετά από 4 επαναλήψεις, αφαιρέστε την 1η καταχώρηση από το τέλος της στοίβας εάν τέλος για Μπορείτε να γράψετε ένα ειδικό πρόγραμμα για να προσδιορίσετε το μέγεθος του παραθύρου γραφικών. Για να γίνει αυτό, αρκεί να ακολουθήσετε ακριβώς τα ίδια βήματα όπως στον Αλγόριθμο 2.2.2, αλλά αντί να το εμφανίσετε στην οθόνη, πρέπει να παρακολουθείτε τις μικρότερες και μεγαλύτερες τιμές των x και y. Αρχικά, ορίζουμε αυτές τις τιμές ίσες με το μηδέν: xtrn xmax = O, ymin = γωνίες = 0. Κάθε φορά που εμφανίζεται ένα νέο σημείο (x, y), ενημερώνονται οι διαστάσεις του παραθύρου: xtrn = iain(x,xmin), xmax = ma.x( x, xtah),

34 34 Κεφάλαιο 2 / Κλασικά Fractals Fig Snowflake μετά από 3 επαναλήψεις (Jong By Kim) ymin min(?/, ymin), utah = max.(y,ymax). Οι τιμές xmin, xmax, ymin και utah που λαμβάνονται στο τέλος του αλγορίθμου χρησιμοποιούνται για την προετοιμασία του παραθύρου εξόδου γραφικών της χελώνας. Δημιουργία κανόνων για συστήματα L. Οι κανόνες δημιουργίας για τα συστήματα L παρατίθενται με αλφαβητική σειρά. Δράκος Harter-Heightway (Εικ. 2.14): αξίωμα = FX newf = F newx = X+YF+ newy = FX Y

35 2.2 L-systems " 35 Fig Flower μετά από 3 επαναλήψεις (Brandon Nelson) Χαλί Sierpinski (Εικ. 2.4): αξίωμα = FXF FF FF newf = FF newx = FXF++FXF++FXF Καμπύλη Hilbert που γεμίζει το επίπεδο (Εικ. 22. ): αξίωμα = X newf = F newx = -YF+XFX+FYnewy = +XF-YFY-FX+ καμπύλη Gosper που γεμίζει το επίπεδο (Εικ. 2.26): αξίωμα = XF newf = F newx = X+YF++YF -FX FXFX-YF+

36 36 Κεφάλαιο 2 / Κλασικά φράκταλ newy = -FX+YFYF++YF+FX FX-Y 0 = tg/3 Καμπύλη Peano, γεμίζοντας το επίπεδο (Εικ. 2.22, 2.23): αξίωμα = F newf = F-F+F+ F+F-F-F-F+F Q = 7g/4 9 = IT/2 Καμπύλη Sierpinski, επίπεδο πλήρωσης (Εικ. 2.25): αξίωμα = F+XF+F+XF newf = F newx = XF-F+F-XF+F +XF-F+F-X a = tg/4 0 = tg/2 Bush (Εικ. 2.16): αξίωμα = F newf = -F+F+[+F-F-]-[-F+F+F] 6> = 7g /8 Μωσαϊκό (Εικ. 2.11): αξίωμα = F-F-F-F newf = F-b+FF-F-FF-Fb-FF+b-FF+F+FF+Fb+FFF newb = bbbbbb Island (Εικ. 2.10): αξίωμα = F+F+F+F newf = F+F-F-FFF+F+F-F 6> = 7g/2 Νιφάδα χιονιού (Εικ. 2.17): αξίωμα = [F]+[F]+[F]+[F]+ [F]+[F] newf = F[++F][-FF]FF[+F][-F]FF (9 = 7g/3 Koch Snowflake (Εικ. 2.2): αξίωμα = F++F+ + F newf = F-F++F-F 0 = 7r/2 Weed (Εικ. 2.15): αξίωμα = F

37 2.2 Συστήματα L 37 Εικ. Δημιουργία κανόνα για άσκηση. 2 newf = F[+F]F[-F]F 0 = tg/7 Λουλούδι (Εικ. 2.18): αξίωμα = F[+F+F][-F-F][++F][ F]F newf = FF[++F][+F][F][-F][F] a =?r/2 c = 7g/1b Αλυσίδα (Εικ. 2.12): αξίωμα = F+F+F+F newf = F +b-F-FFF+F+b-F newb = bbb 0 = tg/2 Ασκήσεις α) Ποια είναι η λέξη στην έξοδο του επόμενου συστήματος L μετά από δύο επαναλήψεις: αξίωμα = F (λέξη αρχικοποίησης) newf =FF-[F] +[F] a = tg/2 (αρχική κατεύθυνση) β) Να παραστήσετε γραφικά τη λέξη που βρέθηκε στην προηγούμενη παράγραφο.

38 38 Κεφάλαιο 2 / Κλασικά φράκταλ 2. Γράψτε ψευδοκώδικα για συστήματα L (χρησιμοποιώντας «newf», κ.λπ.) που εφαρμόζουν τους κανόνες στο Σχ. Βάλτε αξίωμα = F. 3. Κατασκευάστε συστήματα L για φράκταλ από το Π.χ. 1, p Εμφανίστε το αποτέλεσμα του συστήματος L σε ένα γράφημα. 4. Επινοήστε και εφαρμόστε τρία νέα συστήματα L σε έναν υπολογιστή, το αποτέλεσμα των οποίων θα ήταν οι δικές σας εκδόσεις των παρακάτω σχημάτων: α) μια νιφάδα χιονιού ή ένα νησί (με περίγραμμα χωρίς σπασίματα). β) μωσαϊκό ή νησιά (με ασυνεχές όριο). γ) θάμνος ή ζιζάνιο. 5. (Πείραμα υπολογιστή.) Εξερευνήστε από την άποψη των ιδιοτήτων φράκταλ ένα από τα πολλά αντικείμενα που παρουσιάζονται στο αντικείμενο. Πιθανά θέματα: α) φυτά με διασταυρούμενη επικονίαση (ταξιανθίες). β) μωσαϊκό? γ) ανατολίτικο στολίδι. δ) Φράκταλ μουσική Cantor Dust Το κλασικό σετ Cantor, ή Cantor dust, πήρε το όνομά του από τον Georg Cantor, ο οποίος το περιέγραψε το 1883. Η ύπαρξη σκόνης Cantor είχε σημειωθεί παλαιότερα από τον Henry Smith το 1875 ή νωρίτερα. Αυτό το σύνολο είναι πολύ γνωστό στους μαθητές από το μάθημα της μαθηματικής ανάλυσης ως παράδειγμα ενός συνόλου μηδενικού μέτρου Lebesgue, του οποίου η καρδινάτητα είναι ίση με την καρδινάτητα του συνεχούς. Οι ιδιότητες φράκταλ της σκόνης Cantor έχουν μεγάλη σημασία, ειδικά επειδή πολλά γνωστά φράκταλ είναι στενοί συγγενείς αυτού του συνόλου. Η κατασκευή της κλασικής σκόνης Cantor ξεκινά με την απόρριψη του μεσαίου τρίτου (χωρίς τα άκρα) ενός τμήματος μονάδας. Δηλαδή, το αρχικό σύνολο είναι ένα τμήμα και το πρώτο βήμα είναι να αφαιρέσετε το ανοιχτό διάστημα (1/3,2/3). Στο επόμενο και σε όλα τα άλλα βήματα, πετάμε το μεσαίο τρίτο (χωρίς τα άκρα) όλων των τμημάτων του τρέχοντος επιπέδου. Έτσι, λαμβάνουμε (Εικ. 2.20) μια ακολουθία συνόλων:

39 2.3 Σκόνη Cantor 39 Fig Κατασκευή της σκόνης του Cantor Co = d = U C 2 = U U U Το οριακό σύνολο C, που είναι η τομή των συνόλων C n, n = 0,1,2,..., ονομάζεται κλασική σκόνη Cantor . Σε αυτό που ακολουθεί θα το ονομάσουμε απλά Cantor dust. Ιδιότητες της σκόνης καντόρ. 1. Η σκόνη του καντορά είναι ένα ίδιο-όμοιο φράκταλ με διάσταση d = log(2)/log(3) «0,6309, αφού η σχέση Nr d = 1 ισχύει για N 2 και r = 1/3. 2. Η σκόνη Cantor δεν περιέχει διαστήματα θετικού μήκους. Αυτό φαίνεται από την κατασκευή. 3. Το άθροισμα των μηκών των διαστημάτων που αφαιρέθηκαν κατά την κατασκευή του συνόλου C είναι ακριβώς ίσο με 1. Για να το δείξετε, εξετάστε την παρακάτω απόδειξη. Το μήκος του πρώτου διαστήματος που πετάξαμε έξω είναι

40 40 Κεφάλαιο 2 / Τα κλασικά φράκταλ είναι το 1/3. Για να πάρουμε το Cr, απορρίψαμε δύο διαστήματα, το καθένα μήκους 1/3 του 2. Στο επόμενο βήμα, απορρίψαμε 2 2 διαστήματα, το καθένα μήκους 1/3 του 3, κ.λπ. Έτσι, το άθροισμα των μηκών που αφαιρέθηκαν διαστήματα 5 είναι: 5 = 1 /3 + 2/ / p ~ 1 /Z p +. Αλλά αυτή η έκφραση μπορεί να ξαναγραφτεί ως: 5 = (1/3)(1 + 2/3 + (2/3) 2 + (2/3) 3 +), και χρησιμοποιώντας τον τύπο για το άθροισμα μιας γεωμετρικής προόδου, Δηλαδή, παίρνουμε 1: Μπορούμε να υποθέσουμε ότι αν έχει μείνει κάτι στο C μετά την αφαίρεση όλων αυτών των διαστημάτων, τότε μάλλον όχι πολύ. Ωστόσο, αυτό δεν συμβαίνει, κάτι που επιβεβαιώνεται από την ακόλουθη ιδιότητα. 4. Ένα εκπληκτικό αποτέλεσμα της σύγκρισης του συνόλου Cantor με το διάστημα είναι ότι οι καρδινότητες αυτών των συνόλων είναι ίσες. Δύο σύνολα έχουν ίση πληθώρα αν υπάρχει αντιστοιχία ένα προς ένα μεταξύ των σημείων αυτών των συνόλων. Στην περίπτωση των πεπερασμένων συνόλων, αυτή η δήλωση είναι ασήμαντη. Για άπειρα σύνολα, όπως ένα διάλειμμα ή ένα σετ Cantor, η έννοια της καρδινικότητας απαιτεί προσεκτικό χειρισμό. Ως απλή απεικόνιση των όσων ειπώθηκαν, αρκεί να σημειωθεί ότι τα τμήματα και είναι ίσου πάχους, παρά το γεγονός ότι το δεύτερο διάστημα είναι διπλάσιο από το πρώτο. Η αντιστοιχία ένα προς ένα σε αυτή την περίπτωση δίνεται από την αντιστοίχιση /(x) = 2x, όπου x. Πριν προχωρήσουμε στην απόδειξη του κύριου θεωρήματος σχετικά με την καρδινάτητα του συνόλου Cantor, ας θυμηθούμε πώς να αναπαραστήσουμε το σημείο x ενός τμήματος στο σύστημα αριθμών με βάση N, N > 2. Ας διαιρέσουμε το τμήμα σε N ίσα διαστήματα, καθένα μήκους 1/Ν. Ας αριθμήσουμε αυτά τα διαστήματα ως εξής: 0,1,2,..., N 1. Αν αποδειχτεί ότι το σημείο x ανήκει στο διάστημα με αριθμό 5, τότε ορίζουμε xi = 5. Στη συνέχεια διαιρούμε αυτό το διάστημα σε Ν νέο διαστήματα, καθένα μήκους 1/ iV 2. Ας αριθμήσουμε αυτά τα διαστήματα όπως πριν:

41 2.3 Cantor's Dust 41 0,1,2,...,N 1. Αν το σημείο x ανήκει σε ένα νέο διάστημα με αριθμό 3, τότε έστω x% = 3. Συνεχίζοντας με αυτόν τον τρόπο, παίρνουμε μια άπειρη ακολουθία (α: n)^L x, και κάθε τιμή x n ορίζει ένα διάστημα που περιέχει το x στο nο βήμα της διαδικασίας κατάτμησης. Ως αποτέλεσμα, ο αριθμός x μπορεί να αναπαρασταθεί με μια άπειρη ακολουθία: XI X2_ *3_ N + N 2 + N 3 "και κάθε τέτοια παράσταση αντιστοιχεί σε ένα ορισμένο σημείο του τμήματος. Γράφεται εν συντομία ως εξής: x = 0,2 : 1X2X3... (με βάση 7V) και ονομάζεται η αναπαράσταση του x στο αριθμητικό σύστημα με βάση το Ν ή στο σύστημα TV-ary. είναι μια ειδική περίπτωση αυτού του ορισμού. Ας δώσουμε προσοχή σε πολλές μαθηματικές πτυχές που απαιτούν ιδιαίτερη προσοχή Πρώτον, ορισμένοι αριθμοί έχουν περισσότερες από μία αναπαραστάσεις IV. Πρόκειται για αριθμούς της μορφής j/n k, όπου j και k είναι θετικοί ακέραιοι αριθμοί Για τέτοιους αριθμούς, μπορούν να καθοριστούν δύο αναπαραστάσεις IV: η μία τελειώνει με όλα τα μηδενικά και η άλλη με όλα τα N 1 Για παράδειγμα, το x = 1/2 στο δυαδικό σύστημα μπορεί να αναπαρασταθεί με το 2 με δύο τρόπους: 1/ 2 = 0, /2 = 0, Οποιοσδήποτε αριθμός άλλου τύπου εκτός από το j/n k γράφεται στο σύστημα αριθμών IV με μοναδικό τρόπο. Επίσης, αφήσαμε αναπάντητο το ερώτημα εάν μια αυθαίρετη αναπαράσταση IV αντιστοιχεί σε μια μοναδική Χ/. Αυτά τα ζητήματα επιλύονται με τον ίδιο ακριβώς τρόπο όπως στην περίπτωση του συνηθισμένου δεκαδικού συμβολισμού. 2 Διατηρήσαμε τη σημείωση που χρησιμοποιεί ο συγγραφέας για ένα άπειρο περιοδικό κλάσμα.

42 42 Κεφάλαιο 2 / Κλασικά φράκταλ Θεώρημα Η ισχύς του συνόλου Cantor C είναι ίση με τη δύναμη του συνεχούς. Απόδειξη. Πρέπει να δημιουργήσουμε μια αντιστοιχία ένα προς ένα μεταξύ σημείων από το C και σημείων στο τμήμα. Για να γίνει αυτό, πρέπει να εξετάσουμε δυαδικές (βάση 2) καθώς και τριαδικές (βάση 3) αναπαραστάσεις σημείων στο τμήμα. Για να αποφευχθεί η ασάφεια στην περίπτωση που ένα σημείο έχει δύο δυαδικές ή τριαδικές παραστάσεις, θα επιλέγουμε πάντα την αναπαράσταση που τελειώνει με όλες στη δυαδική περίπτωση και με όλες τις δύο στην τριαδική περίπτωση. Σημειώνουμε ότι ένα σημείο εμπίπτει στο σύνολο Cantor C αν και μόνο αν δεν υπάρχουν κανένα στην τριμερή του παράσταση, δηλαδή όταν περιέχει μόνο μηδενικά και δύο. Τότε η επιθυμητή αντιστοιχία σημείων από το C με σημεία του τμήματος επιτυγχάνεται αντικαθιστώντας όλα τα δύο στην τριμερή παράσταση του x με ένα. Η δυαδική αναπαράσταση που λαμβάνεται με αυτόν τον τρόπο ορίζει έναν ορισμένο πραγματικό αριθμό y. Για παράδειγμα, αν το x C είναι: x = 0, (στο τριμερές σύστημα), τότε θέτουμε y = 0, (στο δυαδικό σύστημα). Η περιγραφόμενη διαδικασία καθορίζει μια αντιστοιχία ένα προς ένα μεταξύ x 6 C και y. 5. Το Classical Cantor dust είναι ένα παράδειγμα συμπαγούς, τέλειου και εντελώς ασυνεχούς συνόλου. Αυτές οι έννοιες εξηγούνται στο Κεφάλαιο 3. Επιπλέον, μπορεί να υποστηριχθεί ότι τοπολογικά το κλασικό σύνολο Cantor ορίζεται ως ένα συμπαγές, τέλειο και εντελώς ασυνεχές σύνολο. Αυτό σημαίνει ότι κάθε συμπαγές, τέλειο και εντελώς ασυνεχές σύνολο μπορεί να μετατραπεί συνεχώς σε σκόνη Cantor και υπάρχει ένας αντίστροφος μετασχηματισμός που μπορεί να χρησιμοποιηθεί για την αποκατάσταση του αρχικού σετ. Οποιοδήποτε τέτοιο σύνολο συνήθως ονομάζεται σύνολο Cantor. Δεν πρέπει να πιστεύει κανείς, ωστόσο, ότι όλα τα σετ Cantor είναι ίδια. Επιπλέον, ακόμη και η φράκταλ διάσταση διαφορετικών αυτοπαρόμοιων συνόλων Cantor δεν είναι απαραίτητα η ίδια, όπως δείχνει το ακόλουθο παράδειγμα.

Υπουργείο Παιδείας και Επιστήμης της Ρωσικής Ομοσπονδίας ΟΜΟΣΠΟΝΔΙΑΚΟΣ ΚΡΑΤΙΚΟΣ ΠΡΟΫΠΟΛΟΓΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΤΡΙΤΟΒΑΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ «SARATOV NATIONAL RESEARCH STATE UNIVERSITY»

Τμήμα Πληροφοριακών Συστημάτων και Τεχνολογιών http://chair36.msiu.ru N.V. Lukyanova Fractals Fractals Ορισμός φράκταλ Οι έννοιες της γεωμετρίας φράκταλ και φράκταλ που εμφανίστηκαν στα τέλη της δεκαετίας του '70, από τα μέσα της δεκαετίας του '80

Fractals Ορισμός Fractus (λατ.) - που αποτελείται από θραύσματα Ένα φράκταλ (λατ. fractus θρυμματισμένο) είναι ένα απείρως αυτο-όμοιο γεωμετρικό σχήμα, κάθε θραύσμα του οποίου επαναλαμβάνεται καθώς μειώνεται η κλίμακα.

FRACTALS Πολλά φυσικά αντικείμενα και φαινόμενα δεν είναι λεία, αλλά σπασμένα. Ανάμεσά τους είναι φύλλα δέντρων, ακτογραμμή, κεραυνός κ.λπ. Τα συνηθισμένα διαφοροποιήσιμα δεν είναι κατάλληλα για την περιγραφή αυτών των αντικειμένων

ΑΝΑΠΤΥΞΗ ΑΛΓΟΡΙΘΜΩΝ ΓΙΑ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΕΙΚΟΝΩΝ ΤΗΣ ΥΠΟΚΕΙΜΕΝΗΣ ΕΠΙΦΑΝΕΙΑΣ ΜΕ ΒΑΣΗ ΜΕΘΟΔΟΥΣ ΦΡΑΚΤΑΛ ΓΕΩΜΕΤΡΙΑΣ. Βασικές έννοιες και ορισμοί της γεωμετρίας φράκταλ Κατά τη μελέτη της συνάρτησης

ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΤΗΣ ΡΩΣΙΚΗΣ ΟΜΟΣΠΟΝΔΙΑΣ ΚΡΑΤΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ NOVOSIBIRSK ΕΙΔΙΚΟ ΚΕΝΤΡΟ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΙ ΕΡΕΥΝΑΣ Βαθμός μαθηματικών 0 ΟΡΙΑ ΑΚΟΛΟΥΘΙΑΣ Νοβοσιμπίρσκ Διαισθητικό

Τάξη: 7η τάξη. Ενότητα προγράμματος: Πληροφορική Θέμα μαθήματος: Γραφικά υπολογιστών Προγραμματισμένα αποτελέσματα: Βασισμένη στο θέμα εφαρμογή λογικών ενεργειών κατά την επίλυση εκπαιδευτικών προβλημάτων. συστηματοποίηση

Τμήμα Πληροφοριακών Συστημάτων και Τεχνολογιών http://chair36.msiu.ru N.V. Lukyanova Fractals Fractals Μιγαδικοί αριθμοί Οι μιγαδικοί αριθμοί είναι μια επέκταση του συνόλου των πραγματικών αριθμών. Οποιοσδήποτε μιγαδικός αριθμός μπορεί

Share P.G. Kharkov National University of Mechanics and Mathematics Faculty 014 Discrete Mathematics. Σημειώσεις διάλεξης. Πίνακας περιεχομένων. Άλγεβρα συνόλων..1 Η έννοια του συνόλου... 1. Πράξεις σε σύνολα...

Επιστημονικό και πρακτικό συνέδριο του Εθνικού Εκπαιδευτικού Ιδρύματος Γυμνάσιο «Tsaritsynskaya 1» Fractal graphics Ολοκληρώθηκε από: μαθητές της 8ης τάξης Επικεφαλής: Shevchenko T.I. Volgograd, 2014 Συνάφεια της εργασίας: Τελευταία γεγονότα στον τομέα

Θέμα 4. ΑΡΙΘΜΗΤΙΚΗ ΛΥΣΗ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ -1- Θέμα 4. ΑΡΙΘΜΗΤΙΚΗ ΛΥΣΗ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 4.0. Δήλωση του προβλήματος Το πρόβλημα της εύρεσης των ριζών μιας μη γραμμικής εξίσωσης της μορφής y=f() συναντάται συχνά στην επιστημονική

Θέμα. Εξισώσεις με μέτρο Περιεχόμενα.. Συντελεστής.. Οι απλούστερες εξισώσεις με συντελεστή.. Μέθοδος διαστημάτων.. Συντελεστής Η απόλυτη τιμή (μέτρο) ενός αριθμού είναι η απόσταση στη γραμμή συντεταγμένων από ένα σημείο σε

6. Βασικά στοιχεία γεωμετρίας φράκταλ. 6.1. Η έννοια των φράκταλ αντικειμένων. 6.2 Φράκταλ διάσταση. 6.2.1 Διάσταση ομοιότητας. 6.2.2. Διάσταση Hausdorff-Besikovich. 6.2.3. Διάσταση Minkowski. 6.3

Τα μαθηματικά, όταν τα δούμε σωστά, αντικατοπτρίζουν όχι μόνο την αλήθεια, αλλά και την απαράμιλλη ομορφιά. Μπέρτραντ Ράσελ. Η παρουσίαση δημιουργήθηκε από έναν μαθητή της 11ης τάξης «Β» GUSEV ALEXANDER Φυσικά, ακούσατε

Εξισώσεις Στην άλγεβρα θεωρούνται δύο τύποι ισοτήτων: ταυτότητες και εξισώσεις. Ταυτότητα είναι μια ισότητα που ικανοποιείται για όλες τις έγκυρες) τιμές των γραμμάτων που περιλαμβάνονται σε αυτήν. Για τις ταυτότητες, χρησιμοποιούνται σημάδια

Κεφάλαιο 1 ΟΛΟΚΛΗΡΩΜΕΝΕΣ ΕΞΙΣΩΣΕΙΣ Διάλεξη 1 1 Εισαγωγή Μια εξίσωση ονομάζεται ολοκλήρωμα εάν η άγνωστη συνάρτηση εισέλθει στην εξίσωση κάτω από το ολοκλήρωμα.

Κεφάλαιο 0 ΑΚΟΛΟΥΘΙΑ Αλγόριθμοι Α- Ρύθμιση αριθμητικών ακολουθιών Α- Αριθμητική πρόοδος Α- Γεωμετρική πρόοδος Α- Άθροιση Α-5 Απεριόριστα φθίνουσα γεωμετρική πρόοδος

Επίλυση μη γραμμικών εξισώσεων Όχι πάντα αλγεβρικές ή υπερβατικές εξισώσεις μπορούν να λυθούν επακριβώς.

Μέθοδος Euler Το πρόβλημα της εύρεσης μιας συγκεκριμένης λύσης στη διαφορική εξίσωση () f (6.) μπορεί να λυθεί κατά προσέγγιση με αριθμητικές μεθόδους. Να βρεθεί μια συγκεκριμένη λύση στην εξίσωση (6.) στο διάστημα [ α

Μαθηματική μοντελοποίηση αντικειμένων θερμοηλεκτρικής μηχανικής Διάλεξη 1 Μη γραμμικές αλγεβρικές και υπερβατικές εξισώσεις. Όροι και έννοιες 2 Η μοντελοποίηση είναι η μελέτη ενός αντικειμένου ή συστήματος αντικειμένων από

I. V. Yakovlev Υλικά για τα μαθηματικά MathUs.ru Τετραγωνικές εξισώσεις και ανισώσεις με παραμέτρους. Αυτό το άρθρο είναι αφιερωμένο στη θέση των ριζών ενός τετραγωνικού τριωνύμου ανάλογα με την παράμετρο.

Ενότητα Διαφορικός λογισμός συναρτήσεων μιας και πολλών μεταβλητών Συνάρτηση πραγματικού ορίσματος Πραγματικοί αριθμοί Οι θετικοί ακέραιοι ονομάζονται φυσικοί αριθμοί Προσθήκη σε φυσικούς αριθμούς

STORY ABOUT FRACTALS S.V. Grigoriev και E.G. Yashina Ορισμός φράκταλ Αυστηρός ορισμός: Ένα φράκταλ είναι ένα σύνολο του οποίου η διάσταση Hausdorff-Besicovitch (D F) είναι αυστηρά μεγαλύτερη από την τοπολογική

ΔΙΑΛΕΞΗ 5Β Τοπολογικοί χώροι 3. Μερική τάξη. Οι μικρότερες τοπολογίες. Οδηγίες 1. Μερική σειρά Ας θυμηθούμε τον Ορισμό. Λένε ότι στο σύνολο R δίνεται μια μερική σχέση τάξης,

Όρια και συνέχεια. Όριο συνάρτησης Έστω η συνάρτηση = f) να οριστεί σε κάποια γειτονιά του σημείου = α. Επιπλέον, στο ίδιο το σημείο α η συνάρτηση δεν ορίζεται απαραίτητα. Ορισμός. Ο αριθμός b ονομάζεται όριο

ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΗ 4 Θέμα 1 ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΣΥΝΟΛΩΝ Διάλεξη 1 Σύνολα 6 Διάλεξη Αριθμητικά σύνολα 14 Διάλεξη 3 Πρόσωπα αριθμητικών συνόλων 1 Διάλεξη 4 Σύνολο μιγαδικών αριθμών 7 Θέμα ΘΕΩΡΙΑ ΟΡΙΩΝ Διάλεξη

ΚΕΦΑΛΑΙΟ 1. Προβολική γεωμετρία 1.1. Προβολικός χώρος Ας μας δοθεί ένας (n + 1)-διάστατος διανυσματικός χώρος V (6.1, μέρος I) και ένα μη κενό σύνολο P αυθαίρετης φύσης. Το σύνολο Ρ λέγεται ότι είναι προικισμένο

ΚΡΑΤΙΚΟ ΠΟΛΥΤΕΧΝΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΓΙΑΣ ΠΕΤΡΟΥΒΟΥΡΓΗΣ Τμήμα Ραδιοφυσικής Lebedev B.B. Εύρεση συχνοτήτων συντονισμού και μέτρηση μοτίβων ακτινοβολίας στο εργαστήριο φράκταλ κεραιών Minkowski

ΜΕΤΑΒΛΗΤΕΣ ΚΑΙ ΣΤΑΘΕΡΕΣ ΠΟΣΟΤΗΤΕΣ Ως αποτέλεσμα της μέτρησης φυσικών μεγεθών (χρόνος, εμβαδόν, όγκος, μάζα, ταχύτητα κ.λπ.), καθορίζονται οι αριθμητικές τους τιμές. Τα μαθηματικά ασχολούνται με τις ποσότητες, αποσπάται η προσοχή

Μέτρα Hausdorff Ας ξεκινήσουμε με μερικές κατευθυντήριες σκέψεις. Θυμηθείτε (βλ. διάλεξη) ότι το εξωτερικό μέτρο Lebesgue ενός υποσυνόλου A R n προσδιορίζεται από τον τύπο λ n(a) = inf λ n (P i) : A i P i, P i P, όπου P είναι η κλάση όλων

Περίπου μία οικογένεια νευρώνων με περιορισμένη πολυπλοκότητα αμοιβαίας αναδιάταξης A.P. Sokolov Εισαγωγή Οι συναρτήσεις κατωφλίου της λογικής άλγεβρας είναι ένα μαθηματικό μοντέλο νευρώνων. Έχουν ενδιαφέρον λόγω

Γραφικά ράστερ, διανυσματικά και φράκταλ Τα γραφικά υπολογιστών είναι ένας ειδικός τομέας της επιστήμης των υπολογιστών που μελετά μεθόδους και τεχνικές για τη δημιουργία και την επεξεργασία εικόνων σε μια οθόνη υπολογιστή χρησιμοποιώντας ειδικές

Ανάλυση του προβλήματος «Μάθημα Φυσικής Αγωγής» Η πρώτη παρατήρηση, η οποία απλοποιεί σημαντικά την κατανόηση της λύσης αυτού του προβλήματος, είναι ότι μας ενδιαφέρει μόνο η αναλογία των δυνάμεων των υπολοίπων μαθητών με τη δύναμη του Κόλια, αλλά όχι

Διάλεξη 13: Ταξινόμηση τετράγωνων στο επίπεδο Ομοσπονδιακό Πανεπιστήμιο Ural, Institute of Mathematics and Computer Science, Department of Algebra and Discrete Mathematics Εισαγωγικές παρατηρήσεις Στα προηγούμενα τρία

ΔΙΑΛΕΞΗ 6Α Τοπολογικοί χώροι 2. Κατευθύνσεις 1. Μερική σειρά Ας θυμηθούμε τον Ορισμό. Μια σχέση μερικής τάξης λέγεται ότι δίνεται σε ένα σύνολο R εάν για μερικά ζεύγη (x, y) στοιχείων

Ομοσπονδιακή Υπηρεσία Εκπαίδευσης Moscow State University of Geodesy and Cartography (MIIGAiK) ΜΕΘΟΔΙΚΕΣ ΟΔΗΓΙΕΣ ΚΑΙ ΕΡΓΑΣΙΕΣ ΓΙΑ ΑΝΕΞΑΡΤΗΤΗ ΕΡΓΑΣΙΑ στο μάθημα ΑΝΩΤΕΡΑ ΜΑΘΗΜΑΤΙΚΑ Αριθμητικό

Κεφάλαιο 3. ΔΥΝΑΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η μέθοδος δυναμικού προγραμματισμού (DP) βασίζεται στην ιδέα της εξέτασης, μαζί με ένα δεδομένο ατομικό πρόβλημα βελτιστοποίησης, μια ολόκληρη οικογένεια ατόμων

Κεφάλαιο 8 Συναρτήσεις και γραφήματα Μεταβλητές και εξαρτήσεις μεταξύ τους. Δύο μεγέθη ονομάζονται ευθέως αναλογικά αν ο λόγος τους είναι σταθερός, δηλαδή αν =, πού είναι ένας σταθερός αριθμός που δεν αλλάζει με τις αλλαγές

ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος.......................................... 3 Σύμβολα....... ................................ 5 ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ ΤΟΠΟΛΟΓΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΧΑΡΤΟΓΡΑΦΙΕΣ 1. Τοπολογικοί χώροι...... . ..............

Διάλεξη 10. Φράκταλ και χαοτική δυναμική. 1. Η έννοια του συνόλου φράκταλ. Φράκταλ διάσταση. 2. Γεωμετρία παράξενων ελκυστών. 3. Πολυκλασματικά φάσματα. 1. Η έννοια του συνόλου φράκταλ.

Διάλεξη 3 ΒΑΣΙΚΕΣ ΑΛΓΟΡΙΘΜΙΚΕΣ ΔΟΜΕΣ. ΕΙΔΗ ΑΛΓΟΡΙΘΜΩΝ 1. Βασικές αλγοριθμικές δομές. 2. Αναπαράσταση αλγοριθμικών δομών με χρήση εντολών. 3. Συνδυασμοί βασικών εντολών. 4. Βοηθητικό

BBK.4ya7t+.4ya7.6 M5 Το σχολικό βιβλίο περιλαμβάνεται στον ομοσπονδιακό κατάλογο Merzlyak A.G. Μ5 Άλγεβρα: 9η τάξη: εγχειρίδιο για μαθητές γενικών εκπαιδευτικών οργανισμών / Α.Γ. Merzlyak, V.M. Πολιάκοφ. M.: Ventana-Graf, 07. 368

Κεφάλαιο 3 Θεώρημα Jordan Σχέδιο. Κλειστή καμπύλη, μη κλειστή καμπύλη, μη κλειστή καμπύλη χωρίς αυτοτομές, κλειστή καμπύλη χωρίς αυτοτομές, θεώρημα Jordan για μια καμπύλη χωρίς αυτοτομές

Ομοσπονδιακό Πανεπιστήμιο Ural, Institute of Mathematics and Computer Science, Department of Algebra and Discrete Mathematics Ορισμός μιας βάσης Ορισμός Η βάση ενός διανυσματικού χώρου είναι μια διατεταγμένη

Μηχανή Turing 1 Η μηχανή Turing είναι μια μαθηματική έννοια, όχι μια πραγματική υπολογιστική μηχανή. Το MT είναι ένα μαθηματικό μοντέλο μιας υπολογιστικής συσκευής. Το MT προτάθηκε από τον Alan Turing το 1936

Συναρτήσεις πολλών μεταβλητών Σε πολλά ερωτήματα γεωμετρίας, φυσικών επιστημών και άλλων επιστημών, πρέπει κανείς να ασχοληθεί με συναρτήσεις δύο τριών ή περισσότερων μεταβλητών. Παραδείγματα: Εμβαδόν τριγώνου S a h όπου a είναι η βάση

Θέμα Ολόκληρα και κλασματικά μέρη ενός αριθμού Μάθημα 1 (ώρες) Σκοπός του μαθήματος Διδακτική Να εισαγάγει τους μαθητές στο ακέραιο και κλασματικά μέρη ενός αριθμού Να καθορίσει τις ιδιότητες και τις μεταξύ τους σχέσεις Να διδάξει πώς να κατασκευάζει το πιο απλό

Ενότητα 5. Τεχνολογίες Ιστού και σχεδιασμός υπολογιστών 267 UDC 004.921 M.S. Israelyan, V.N. Belovodsky Donetsk National Technical University, Donetsk Department of Computer Monitoring Systems ANALYSIS OF ALGEBRAIC

ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ Οι συναρτήσεις μιας ανεξάρτητης μεταβλητής δεν καλύπτουν όλες τις εξαρτήσεις που υπάρχουν στη φύση. Επομένως, είναι φυσικό να επεκτείνουμε τη γνωστή έννοια της λειτουργικής εξάρτησης και να εισάγουμε

I. V. Yakovlev Υλικά για τα μαθηματικά MathUs.ru Παράμετροι και τετραγωνικό τριώνυμο. 2 Αυτό το άρθρο είναι αφιερωμένο στη θέση των ριζών ενός τετραγωνικού τριωνύμου ανάλογα με την παράμετρο. Υπολογισμός ριζών

Διάλεξη 3. 3. Μέθοδος του Νεύτωνα (εφαπτομένες. Ας ορίσουμε κάποια αρχική προσέγγιση [,b] και γραμμικοποιούμε τη συνάρτηση f(στη γειτονιά χρησιμοποιώντας ένα τμήμα της σειράς Taylor f(= f(+ f "((-. (5 Αντί της εξίσωσης (λύνουμε

UDC 51798868 ΑΡΧΗ ΓΕΝΙΚΕΥΜΕΝΩΝ ΑΝΤΙΘΕΤΩΝ ΧΑΡΤΟΓΡΑΦΙΩΝ ΣΕ ΨΕΥΔΟΜΕΤΡΙΚΟΥΣ ΧΩΡΟΥΣ A I Perov Voronezh State University Κατά τη μελέτη συστημάτων εξισώσεων (αλγεβρικό διαφορικό

Y. S. Ilyashenko Οι ελκυστές και η φράκταλ διάσταση τους MCNM Summer School “Modern Mathematics” Dubna, Ιούλιος 2004 Y. S. Ilyashenko Οι ελκυστές και η φράκταλ διάσταση τους Ηλεκτρονική δημοσίευση Μόσχα, 2016

Θέμα 7 Κατάταξη πίνακα Βασικό δευτερεύον θεώρημα για την κατάταξη ενός πίνακα και οι συνέπειές του Συστήματα m γραμμικών εξισώσεων με αγνώστους Θεώρημα Kronecker-Capelli Θεμελιώδες σύστημα λύσεων ομοιογενούς συστήματος γραμμικών εξισώσεων

Τι άλλο να διαβάσετε

Φράκταλ Xaos. Φράκταλ στη βιολογία. Χρυσή αναλογία, φράκταλ και χάος Διδάκτωρ Φυσικών και Μαθηματικών Επιστημών A. DMITRIEV, Κορυφαίος Ερευνητής στο Ινστιτούτο Ραδιομηχανικής και Ηλεκτρονικής της Ρωσικής Ακαδημίας Επιστημών...

1 3 στην περίοδο. Περιοδικό κλάσμα. Δείτε τι είναι το "Περιοδικό κλάσμα" σε άλλα λεξικά πώς να μετατρέψετε αριθμούς σε περίοδο όπως το 0,(3) σε κανονικό κλάσμα; και πήρα την καλύτερη απάντησηΑπάντηση από τον κανόνα Gold-Silver[guru]...

Η επίδραση περιβαλλοντικών παραγόντων στο σώμα του παιδιού /. Αυξημένη και μειωμένη θερμοκρασία αέρα και περιφράξεων. Οι χώροι παραγωγής χωρίζονται σε: ψυχρούς,...

Φράκταλ Xaos. Φράκταλ στη βιολογία. Χρυσή αναλογία, φράκταλ και χάος

Φράκταλ:

Γεωμετρικά φράκταλ

Αλγεβρικά φράκταλ

Στοχαστικά φράκταλ

Διαχείριση Χάους

Το παιχνίδι της ζωής σε κυψελωτά αυτόματα

Βιολογική εξέλιξη

Αυτοοργανωμένη κρισιμότητα

Παραγωγή πληροφοριών από χαοτικά συστήματα

Καταγραφή, αποθήκευση και ανάκτηση πληροφοριών χρησιμοποιώντας το χάος

Μεταφορά και προστασία πληροφοριών

Αντίγραφο

Τι άλλο να διαβάσετε

ΟΙ ΤΕΛΕΥΤΑΙΕΣ ΣΗΜΕΙΩΣΕΙΣ

Κατηγορίες