모듈러스와의 부등식, USE 솔루션의 예. 간격 방법은 모듈러스를 사용하여 부등식을 해결하는 보편적인 방법입니다. 불평등을 해결한다는 것이 무엇을 의미하는지 설명해보자

숫자의 계수이 숫자 자체가 음수가 아니면 호출되고, 음수이면 반대 부호가 붙은 동일한 숫자라고 합니다.

예를 들어 숫자 6의 모듈러스는 6이고 숫자 -6의 모듈러스도 6입니다.

즉, 숫자의 계수는 부호를 고려하지 않고 이 숫자의 절대값인 절대값으로 이해됩니다.

다음과 같이 지정됩니다: |6|, | 엑스|, |에이| 등.

(자세한 내용은 "숫자 모듈" 섹션을 참조하세요).

모듈러스가 있는 방정식.

실시예 1 . 방정식을 풀어보세요|10 엑스 - 5| = 15.

해결책.

규칙에 따르면 방정식은 두 방정식의 조합과 같습니다.

10엑스 - 5 = 15
10엑스 - 5 = -15

우리는 다음을 결정합니다:

10엑스 = 15 + 5 = 20
10엑스 = -15 + 5 = -10

엑스 = 20: 10
엑스 = -10: 10

엑스 = 2
엑스 = -1

답변: 엑스 1 = 2, 엑스 2 = -1.

실시예 2 . 방정식을 풀어보세요|2 엑스 + 1| = 엑스 + 2.

해결책.

모듈러스는 음수가 아니므로 엑스+ 2 ≥ 0. 따라서:

엑스 ≥ -2.

두 가지 방정식을 만들어 보겠습니다.

2엑스 + 1 = 엑스 + 2
2엑스 + 1 = -(엑스 + 2)

우리는 다음을 결정합니다:

2엑스 + 1 = 엑스 + 2
2엑스 + 1 = -엑스 - 2

2엑스 - 엑스 = 2 - 1
2엑스 + 엑스 = -2 - 1

엑스 = 1
엑스 = -1

두 숫자 모두 -2보다 큽니다. 따라서 둘 다 방정식의 뿌리입니다.

답변: 엑스 1 = -1, 엑스 2 = 1.

실시예 3 . 방정식을 풀어보세요

|엑스 + 3| - 1
————— = 4
엑스 - 1

해결책.

분모가 0이 아닌 경우 방정식은 의미가 있습니다. 즉, 엑스≠ 1. 이 조건을 고려해보자. 첫 번째 작업은 간단합니다. 분수를 제거하는 것이 아니라 변환하여 순수한 형태의 모듈을 얻습니다.

|엑스+ 3| - 1 = 4 · ( 엑스 - 1),

|엑스 + 3| - 1 = 4엑스 - 4,

|엑스 + 3| = 4엑스 - 4 + 1,

|엑스 + 3| = 4엑스 - 3.

이제 방정식의 왼쪽에 있는 계수 아래에 표현식만 있습니다. 계속 진행합시다.
숫자의 모듈러스는 음수가 아닌 숫자입니다. 즉, 0보다 크거나 0과 같아야 합니다. 따라서 우리는 불평등을 해결합니다.

4엑스 - 3 ≥ 0

4엑스 ≥ 3

엑스 ≥ 3/4

따라서 두 번째 조건이 있습니다. 방정식의 근은 최소한 3/4이어야 합니다.

규칙에 따라 우리는 두 개의 방정식 세트를 구성하고 이를 해결합니다.

엑스 + 3 = 4엑스 - 3
엑스 + 3 = -(4엑스 - 3)

엑스 + 3 = 4엑스 - 3
엑스 + 3 = -4엑스 + 3

엑스 - 4엑스 = -3 - 3
엑스 + 4엑스 = 3 - 3

엑스 = 2
엑스 = 0

우리는 두 가지 답변을 받았습니다. 이들이 원래 방정식의 근인지 확인해 봅시다.

두 가지 조건이 있었습니다. 방정식의 근은 1이 될 수 없으며 최소한 3/4이어야 합니다. 즉 엑스 ≠ 1, 엑스≥ 3/4. 얻은 두 가지 답변 중 하나만이 두 조건 모두에 해당합니다(숫자 2). 이는 이것이 원래 방정식의 근본임을 의미합니다.

답변: 엑스 = 2.

모듈러스와의 부등식.

실시예 1 . 불평등 해결| 엑스 - 3| < 4

해결책.

모듈 규칙에는 다음과 같이 명시되어 있습니다.

|에이| = 에이, 만약에 에이 ≥ 0.

|에이| = -에이, 만약에 에이 < 0.

모듈은 음수가 아닌 숫자와 음수를 모두 가질 수 있습니다. 따라서 우리는 두 가지 경우를 모두 고려해야 합니다. 엑스- 3 ≥ 0 및 엑스 - 3 < 0.

1) 언제 엑스- 3 ≥ 0 원래 부등식은 모듈러스 기호 없이 그대로 유지됩니다.
엑스 - 3 < 4.

2) 언제 엑스 - 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:

-(엑스 - 3) < 4.

괄호를 열면 다음을 얻습니다.

-엑스 + 3 < 4.

따라서 이 두 가지 조건으로부터 우리는 두 가지 불평등 시스템을 통합하게 되었습니다.

엑스 - 3 ≥ 0
엑스 - 3 < 4

엑스 - 3 < 0
-엑스 + 3 < 4

문제를 해결해 봅시다:

엑스 ≥ 3
엑스 < 7

엑스 < 3
엑스 > -1

따라서 우리의 대답은 두 세트의 합집합입니다.

3 ≤ 엑스 < 7 U -1 < 엑스 < 3.

가장 작은 것을 결정하고 가장 높은 가치. 이는 -1과 7입니다. 게다가 엑스-1보다 크고 7보다 작습니다.
게다가, 엑스≥ 3. 이는 불평등에 대한 해결책이 이러한 극단 숫자를 제외한 -1부터 7까지의 전체 숫자 집합이라는 것을 의미합니다.

답변: -1 < 엑스 < 7.

또는: 엑스 ∈ (-1; 7).

부가기능.

1) 불평등을 그래픽으로 해결하는 더 간단하고 짧은 방법이 있습니다. 이렇게 하려면 수평 축을 그려야 합니다(그림 1).

표현 | 엑스 - 3| < 4 означает, что расстояние от точки 엑스 3번 지점은 4개 단위 미만입니다. 축에 숫자 3을 표시하고 축의 왼쪽과 오른쪽에 4개의 구분선을 셉니다. 왼쪽에서는 -1 지점, 오른쪽에서는 7 지점으로 이동합니다. 따라서 지점은 엑스우리는 계산하지 않고 그냥 보았습니다.

또한 부등식 조건에 따라 -1과 7 자체는 해 집합에 포함되지 않습니다. 따라서 우리는 답을 얻습니다.

1 < 엑스 < 7.

2) 그러나 그래픽 방식보다 더 간단한 또 ​​다른 솔루션이 있습니다. 이를 위해서는 불평등이 다음과 같은 형식으로 표현되어야 합니다.

4 < 엑스 - 3 < 4.

결국 이것은 모듈러스 규칙에 따른 방법입니다. 음수가 아닌 숫자 4와 유사한 음수 -4는 부등식을 해결하기 위한 경계입니다.

4 + 3 < 엑스 < 4 + 3

1 < 엑스 < 7.

실시예 2 . 불평등 해결| 엑스 - 2| ≥ 5

해결책.

이 예는 이전 예와 크게 다릅니다. 좌변은 5보다 크거나 5와 같습니다. C 기하학적 점관점에서 볼 때 부등식에 대한 해결책은 지점 2에서 5단위 이상 떨어진 모든 숫자입니다(그림 2). 그래프는 이것이 모두 -3보다 작거나 같고 7보다 크거나 같은 숫자임을 보여줍니다. 이는 우리가 이미 답을 받았다는 것을 의미합니다.

답변: -3 ≥ 엑스 ≥ 7.

그 과정에서 우리는 반대 기호를 사용하여 자유 항을 왼쪽과 오른쪽으로 재배열하여 동일한 부등식을 해결합니다.

5 ≥ 엑스 - 2 ≥ 5

5 + 2 ≥ 엑스 ≥ 5 + 2

대답은 동일합니다: -3 ≥ 엑스 ≥ 7.

또는: 엑스 ∈ [-3; 7]

예제가 해결되었습니다.

실시예 3 . 불평등 해결 6 엑스 2 - | 엑스| - 2 ≤ 0

해결책.

숫자 엑스양수, 음수 또는 0일 수 있습니다. 그러므로 우리는 세 가지 상황을 모두 고려해야 합니다. 아시다시피 두 가지 불평등이 고려됩니다. 엑스≥ 0 및 엑스 < 0. При 엑스≥ 0이면 모듈러스 기호 없이 원래 부등식을 있는 그대로 다시 작성합니다.

6x2 - 엑스 - 2 ≤ 0.

이제 두 번째 경우에 대해 설명합니다. 엑스 < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6엑스 2 - (-엑스) - 2 ≤ 0.

대괄호 확장:

6엑스 2 + 엑스 - 2 ≤ 0.

따라서 우리는 두 가지 방정식 시스템을 얻었습니다.

6엑스 2 - 엑스 - 2 ≤ 0
엑스 ≥ 0

6엑스 2 + 엑스 - 2 ≤ 0
엑스 < 0

우리는 시스템의 부등식을 풀어야 합니다. 이는 두 개의 이차 방정식의 근을 찾아야 함을 의미합니다. 이를 위해 부등식의 왼쪽을 0으로 동일시합니다.

첫 번째부터 시작해 보겠습니다.

6엑스 2 - 엑스 - 2 = 0.

이차 방정식을 푸는 방법 - "이차 방정식" 섹션을 참조하세요. 즉시 답변의 이름을 지정하겠습니다.

엑스 1 = -1/2, x 2 = 2/3.

첫 번째 불평등 체계로부터 우리는 원래 불평등에 대한 해가 -1/2에서 2/3까지의 전체 숫자 집합이라는 것을 얻습니다. 우리는 솔루션 조합을 작성합니다. 엑스 ≥ 0:
[-1/2; 2/3].

이제 두 번째 이차 방정식을 풀어보겠습니다.

6엑스 2 + 엑스 - 2 = 0.

그 뿌리:

엑스 1 = -2/3, 엑스 2 = 1/2.

결론: 언제 엑스 < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.

두 가지 답을 결합하여 최종 답을 얻습니다. 답은 이러한 극단 숫자를 포함하여 -2/3에서 2/3까지의 전체 숫자 집합입니다.

답변: -2/3 ≤ 엑스 ≤ 2/3.

또는: 엑스 ∈ [-2/3; 2/3].

검토됨

모스크바 교육 기관 교육위원회

"자시젬스카야 중등학교"

프로토콜 1번

동의함

HR 담당 부국장

_______ /시도르키나 R.L./

나는 승인했다

교장 선생님:

AP 코나코프

주문번호 63

계수를 사용하여 방정식과 부등식 풀기

연구작업

이 프로그램은 다음에 의해 컴파일되었습니다.

고등 수학 선생님

시도르키나 R.L.

Zashizhemye 마을, 2014

목차

소개..........................................................................................................3

모듈러스를 이용한 가장 간단한 방정식과 부등식........................................5

모듈러스를 사용한 방정식 및 부등식의 그래픽 솔루션..........8

모듈러스를 사용하여 방정식과 부등식을 푸는 다른 방법........10

결론...........................................................................16

참고문헌..........................................................................18

1. 소개

절대값(모듈러스)의 개념은 실수와 복소수 분야 모두에서 숫자의 가장 중요한 특성 중 하나입니다.

이 개념은 학교 수학 과정의 다양한 섹션뿐만 아니라 대학에서 공부하는 고등 수학, 물리학 및 기술 과학 과정에서도 널리 사용됩니다. 예를 들어, 대략적인 계산 이론에서는 대략적인 숫자의 절대 및 상대 오류 개념이 사용됩니다. 역학과 기하학에서는 벡터의 개념과 길이(벡터 계수)를 연구합니다. 수학적 분석에서 숫자의 절대값 개념은 극한, 제한된 기능등 절대값과 관련된 문제는 다음에서 자주 발견됩니다. 수학 올림피아드, 대학 입학 시험 및 통합 주 시험.그래서 우리가 이 주제의 몇 가지 측면을 연구하는 것이 중요해졌습니다.

집 목적우리의 작업은 모듈러스를 사용하여 방정식과 부등식을 해결하기 위한 다양한 방법을 연구하는 것입니다.

이 목표는 다음 문제를 해결하여 달성되어야 합니다. 작업:

모듈의 정의와 일부 속성을 연구합니다.

등가 전이를 통해 모듈러스를 사용한 간단한 방정식과 부등식의 해법을 마스터하세요.

계수를 사용하여 방정식과 부등식을 풀기 위한 다양한 방법을 고려하십시오.

물체연구는 모듈러스를 사용한 방정식과 부등식의 일부 유형입니다.

목연구 - 계수를 사용하여 방정식과 부등식을 해결하는 다양한 방법, 즉 그래픽 방법, 기하학적 해석 방법, 항등식 사용, 부호 정리 적용, 결과로의 전환 방법, 간격 방법, 양수 곱셈 방법, 모듈 공개 방법.

연구하는 동안에 관한 문헌을 연구하는 등의 방법 이 문제그리고 실용적인 방법.

작업 과정에서 우리는 다음과 같은 출처를 조사했습니다.

1. 학생 및 학생을 위한 “큰 수학 백과사전”;

수학. 통합 국가 시험 - 2011-2012. 전형적인 시험 옵션. / 편집자: A.L. 세메노바, I.V. 야쉬첸코.

백과사전 “나는 세상을 안다” 수학;

;

1. 1. 모듈러스를 사용한 가장 간단한 방정식 및 부등식

우리는 다음과 같은 등가 전이 중 하나로 해결되는 가장 간단한 방정식을 고려할 것입니다.

간단한 방정식을 푸는 예.

실시예 1 방정식을 풀어보자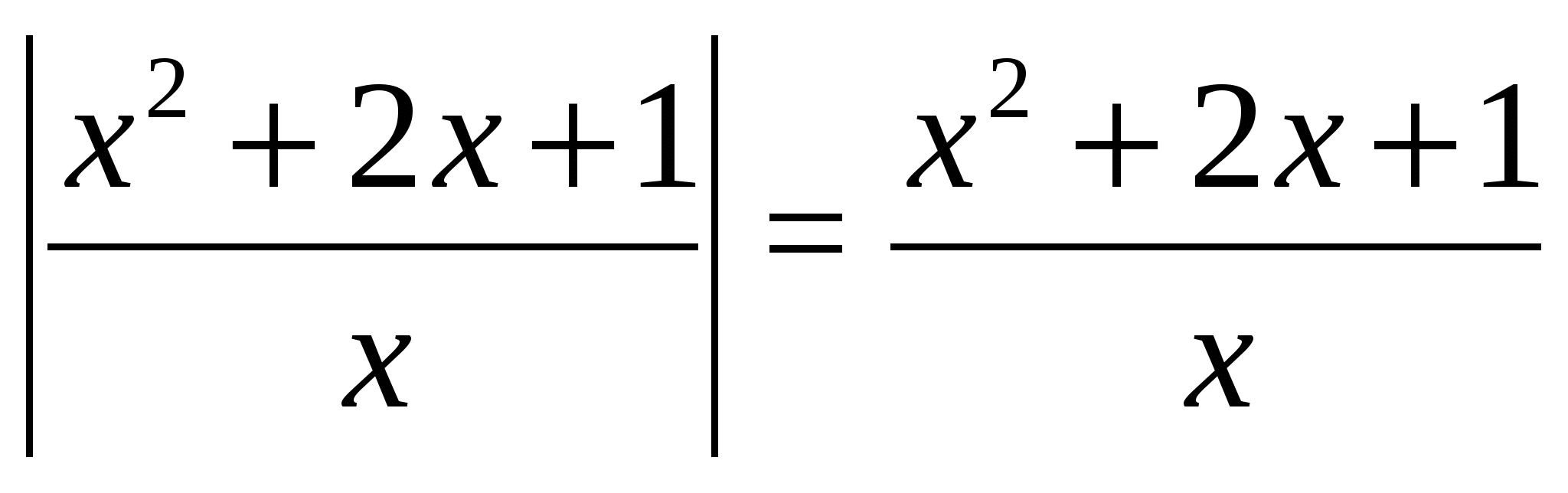
.

해결책.

답변.
.

실시예 2 방정식을 풀어 봅시다.

해결책.

답변.
.

실시예 3 방정식을 풀어보자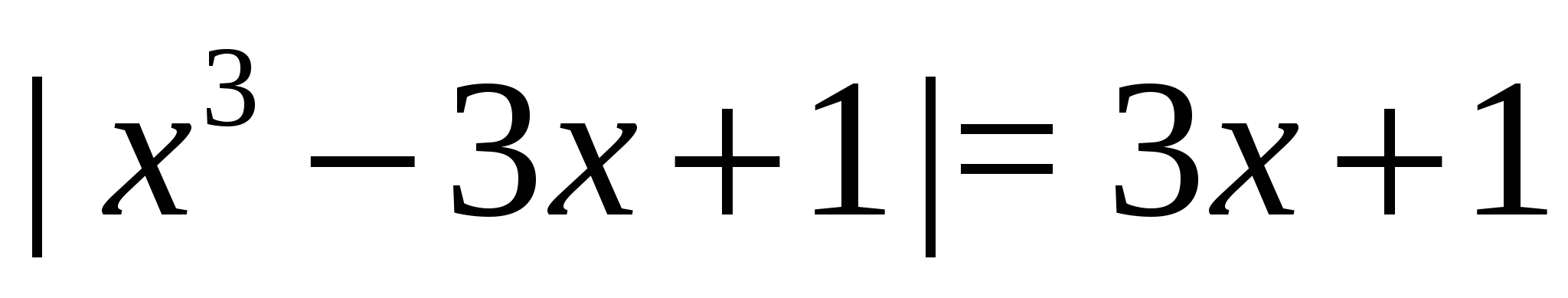
.

해결책.

답변.
.

일련의 방정식은 다음 정리를 사용하여 해결됩니다.

정리 4 모듈의 합은 각 수량에 대수적 합에 포함되는 부호가 있는 경우에만 하위 모듈 수량의 대수적 합과 같습니다.

실시예 5 방정식을 풀어보세요

해결책.이후 , 그러면 우리는 다음과 같은 형식의 동등성을 갖습니다.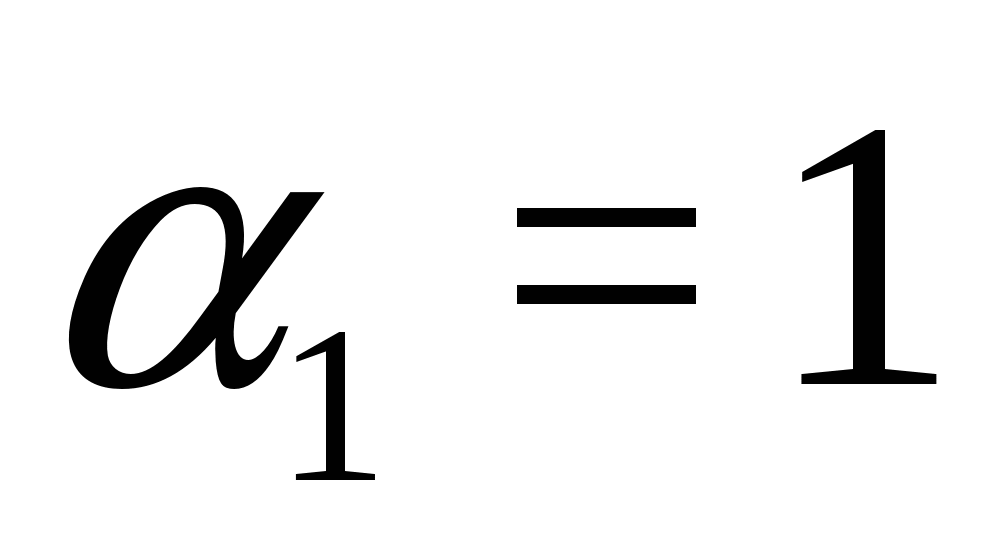
,
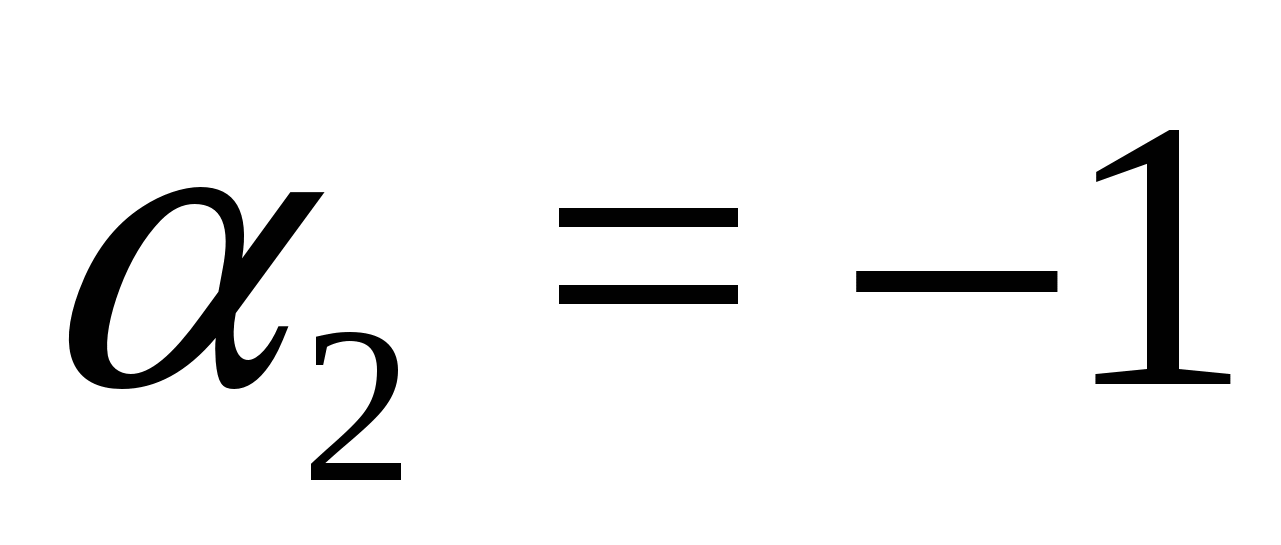. 따라서 원래 방정식은 다음 시스템과 동일합니다.

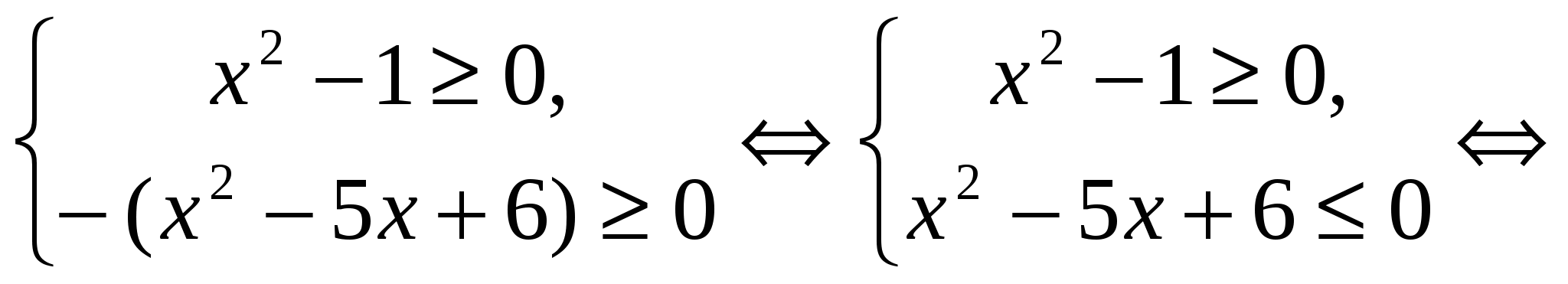
답변.
.

단순 불평등을 해결하는 예.

실시예 6 불평등을 해결하자
.

해결책.

답변.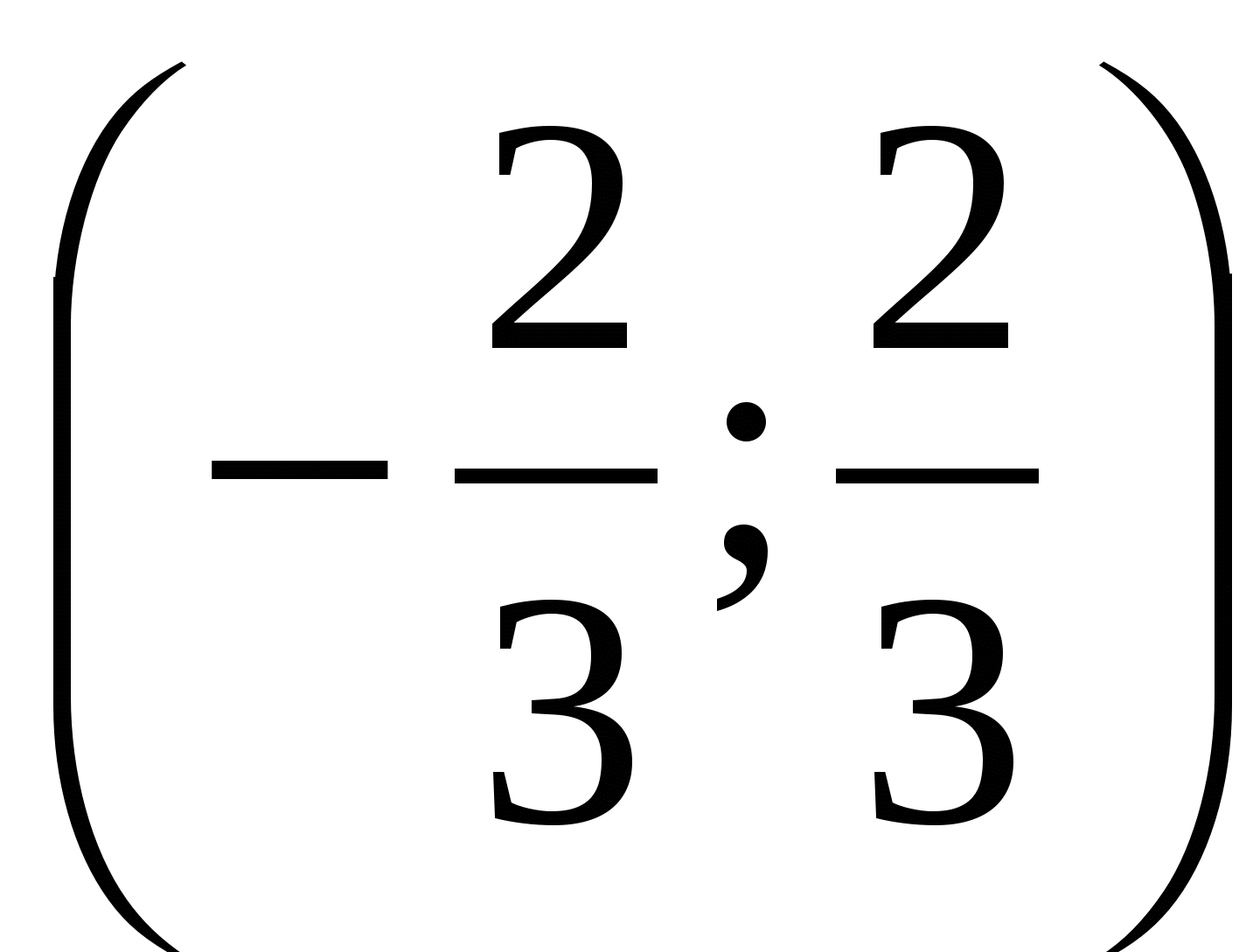
.

실시예 7 불평등을 해결하자
.

해결책.

답변.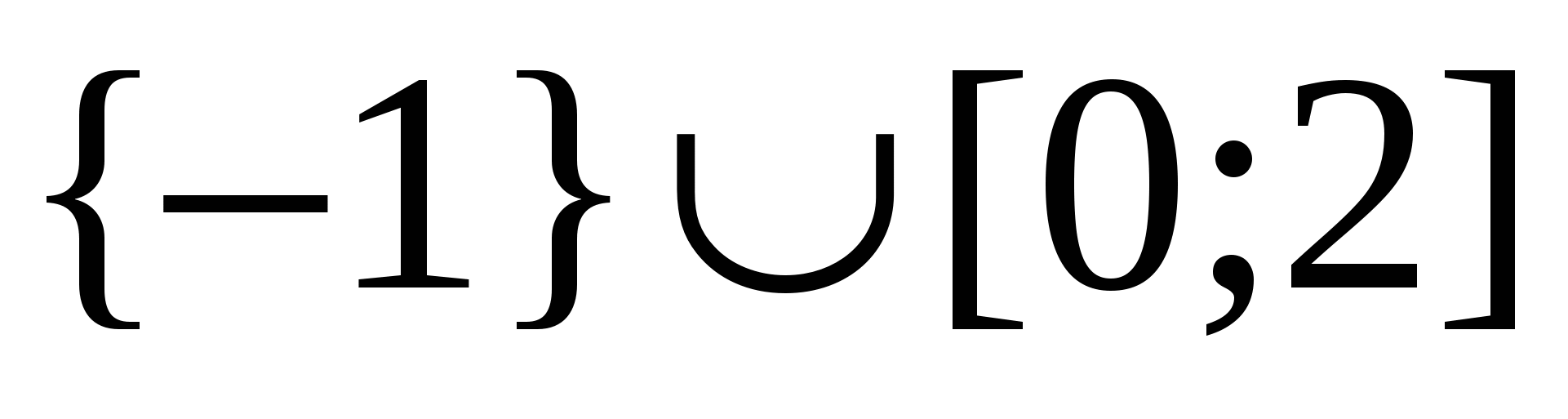
.

이상하게도 충분하지만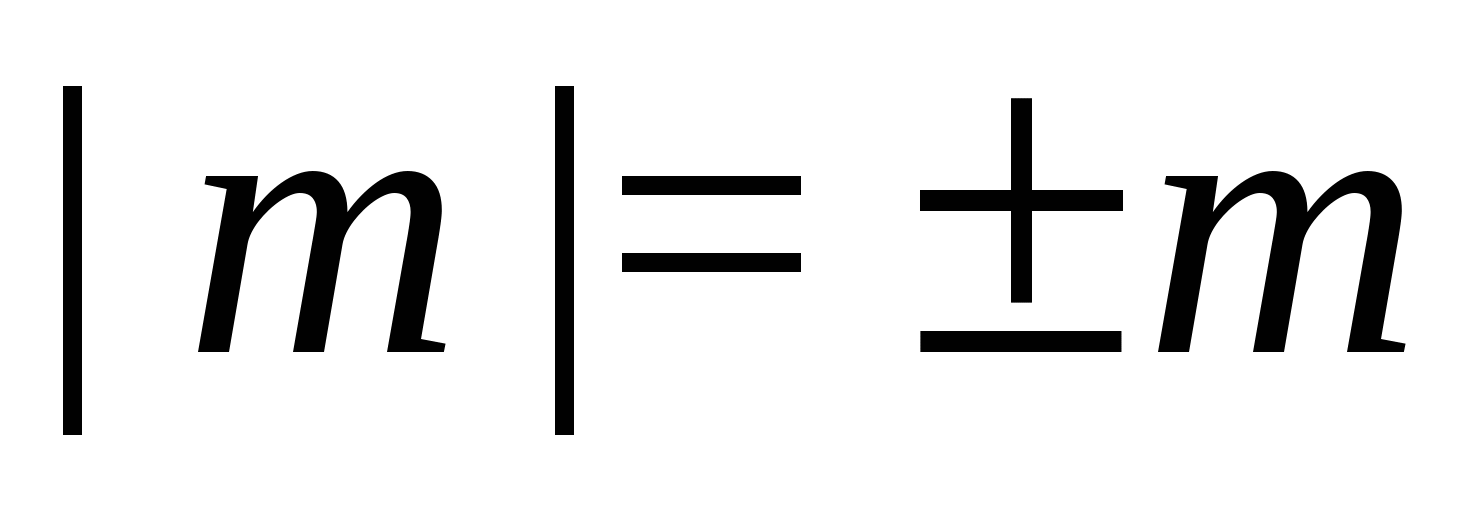
불평등에서 모듈러스 기호를 제거하기에 충분합니다.

실시예 8 불평등 해결

해결책.

답변.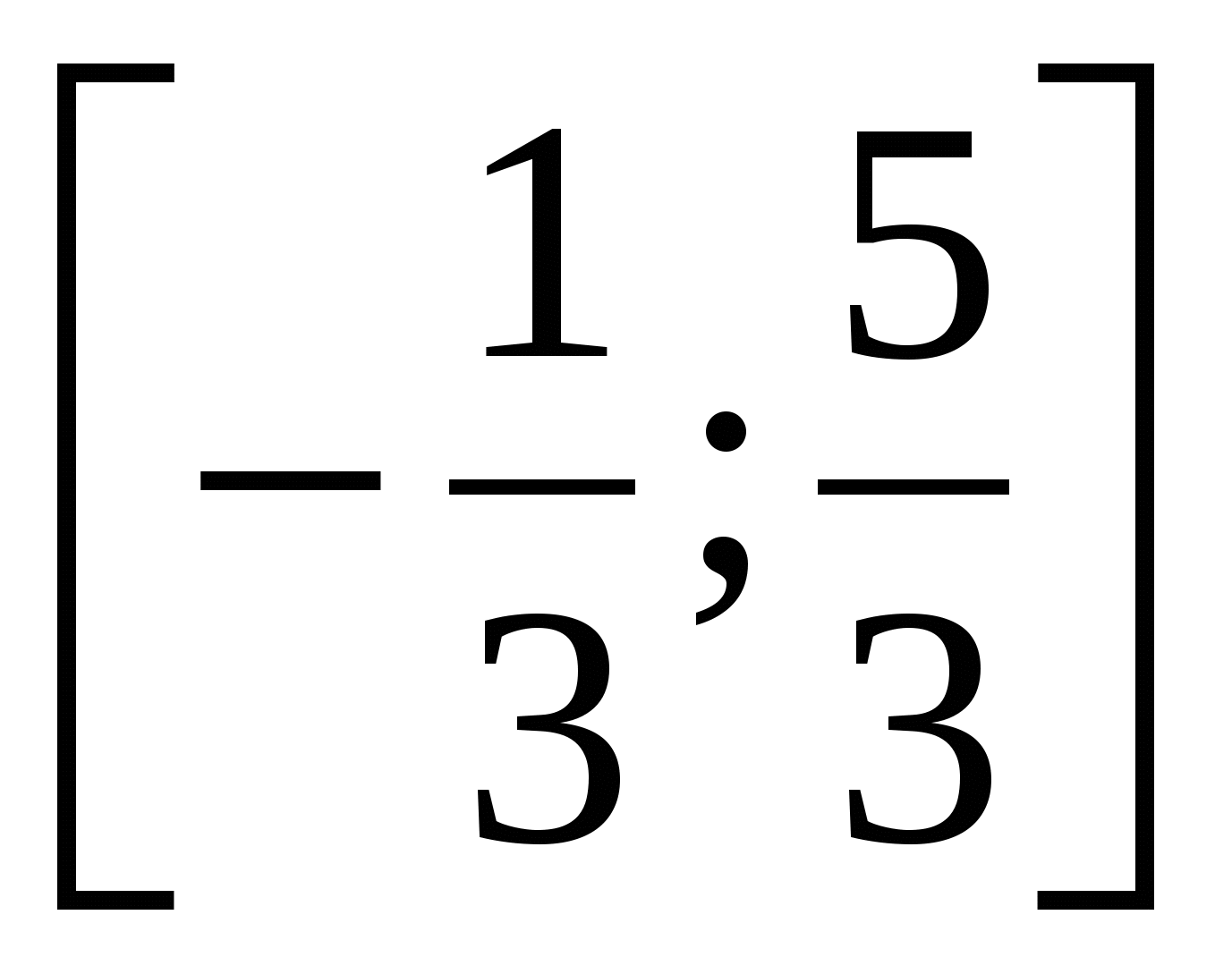
.

3. 계수를 사용한 방정식 및 부등식의 그래픽 솔루션

절대값의 부호가 포함된 방정식을 푸는 것은 분석적으로가 아니라 그래픽으로 푸는 것이 훨씬 더 편리합니다(특히 매개변수가 포함된 방정식).

실시예 9(C5, 통합 상태 시험 - 2010)

기음5. 각 값에 대해에이 방정식의 해 개수를 나타냅니다.

해결책.함수를 그려보자
. 이렇게 하려면 완전한 정사각형을 선택하세요.

함수 y = 그래프의 교차점 수
수평선이 있는 경우 y = a는 방정식의 해 개수와 같습니다.

에 대한 답변: 만약에 < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а >4 그렇다면 해결책은 두 가지입니다.

계수를 사용하여 방정식과 부등식을 해결하는 다른 방법

• 모듈 확장 방법

예제를 사용하여 모듈을 확장하는 방법을 살펴보겠습니다.

실시예 10 방정식을 풀어보세요

해결책.이 방정식에는 둘 이상의 모듈이 포함되어 있습니다.

두 개 이상의 모듈 부호에 변수가 포함된 방정식을 푸는 방법은 다음과 같습니다.

1. 각 모듈이 0이 되는 변수의 값을 찾습니다.
,
;
,
;
,
.

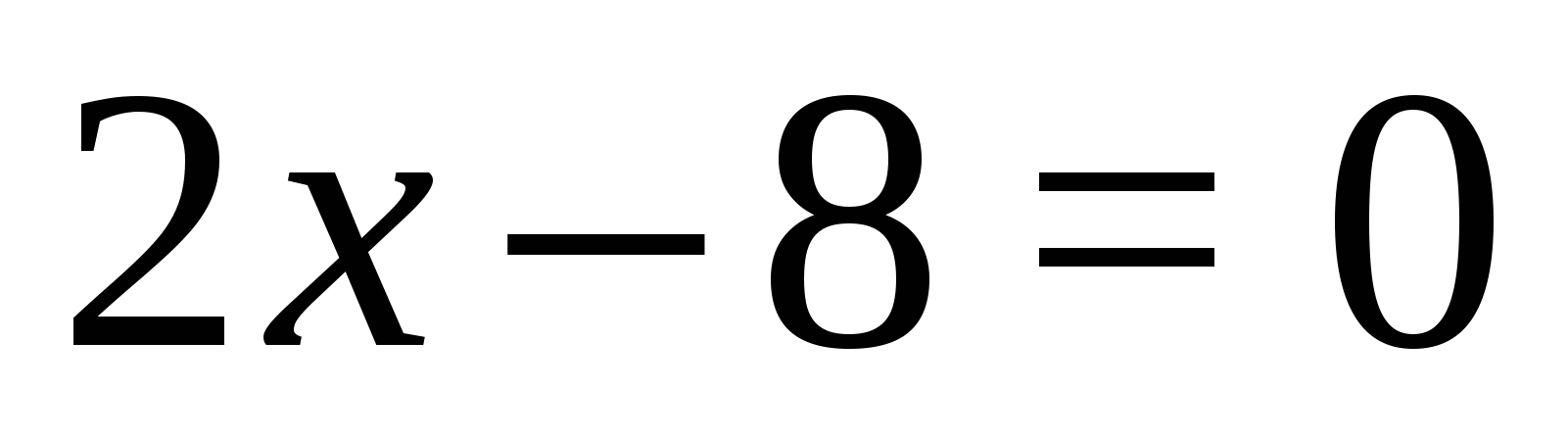2. 이 점들을 수직선에 표시하세요.

3. 각 간격의 방정식을 고려하고 모듈 아래에 있는 표현식의 부호를 설정합니다.

1) 언제
또는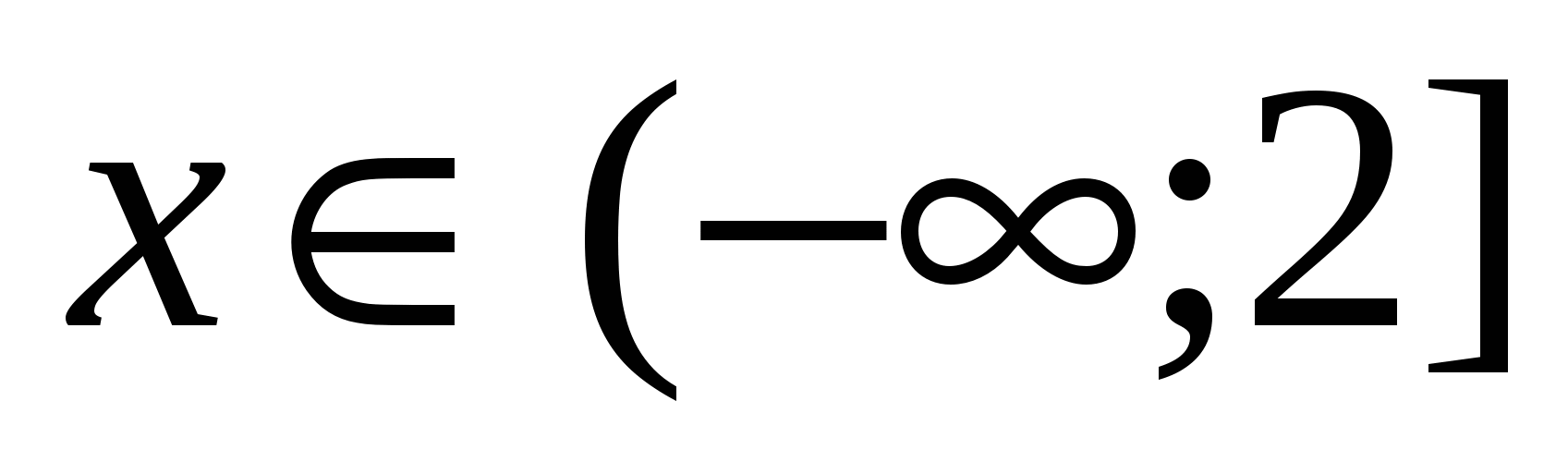
. 이 구간에서 각 모듈로 표현식의 부호를 결정하려면 임의의 값을 취하는 것으로 충분합니다. 이 간격에서 이를 표현식으로 대체합니다. 결과 값이 음수이면 모든 이 간격에서 표현식은 음수가 됩니다. 결과 숫자 값이 양수이면 모든 값에 대해 이 간격에서 표현식은 양수가 됩니다.

값을 받아보자
사이에서
그 값을 표현식에 대체합니다.
, 우리는 얻는다
, 이는 이 간격을 의미합니다.
음수이므로 "마이너스" 기호가 있는 모듈 아래에서 "나올 것입니다"", 우리는 다음을 얻습니다:
.

이 값에서 , 표현
값을 얻을 것이다
, 이는 간격 내에 있음을 의미합니다.
또한 음수 값을 취하고 "마이너스" 기호를 사용하여 모듈을 "종료"하면 다음과 같은 결과를 얻습니다.
.

표현
값을 얻을 것이다
그리고 ``빼기' 기호와 함께 모듈 아래에서 "종료"됩니다:
.

이 구간의 방정식은 다음과 같습니다. 이를 풀면 다음을 알 수 있습니다.
.

이 값이 간격에 포함되어 있는지 확인합니다.
. 포함되어 있음이 밝혀졌습니다.
방정식의 근본입니다.

2) 언제
. 원하는 값을 선택하세요. 이 틈에서. 허락하다
. 이 값에서 모듈러스 아래의 각 표현식의 부호를 결정합니다. . 다음과 같은 표현이 밝혀졌습니다.
긍정적이고 나머지 두 개는 부정적입니다.

이 구간의 방정식은 다음과 같은 형식을 취합니다. 그것을 해결하면 우리는 찾아냅니다.
. 이 값은 범위에 포함되지 않습니다.
이므로 방정식의 근이 아닙니다.

3) 언제
. 임의의 값을 선택하세요 이 간격에서
그리고 각 표현에 대입해 보세요. 우리는 다음과 같은 표현을 발견했습니다.
그리고
긍정적이고
- 부정적인. 우리는 다음 방정식을 얻습니다: .

변환 후에는 다음을 얻습니다.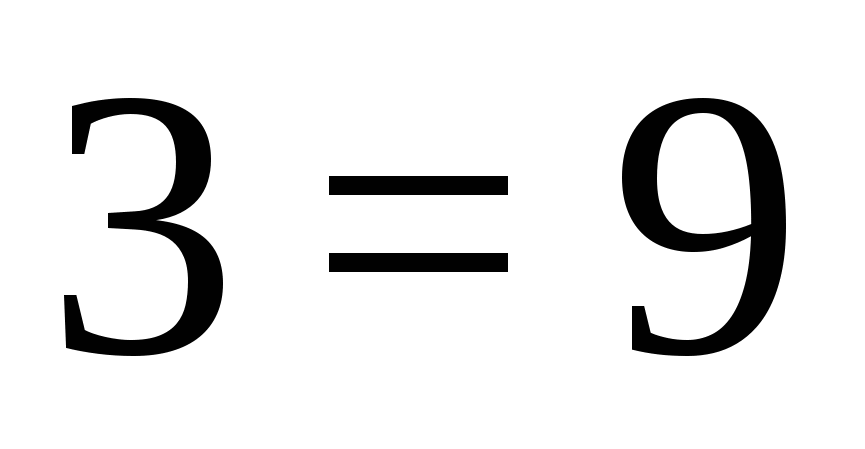
, 이는 방정식에 이 구간에 근이 없음을 의미합니다.

4) 언제
. 이 구간의 모든 표현식이 양수라는 것을 쉽게 알 수 있습니다. 즉, 다음 방정식을 얻습니다.
,
이는 구간에 포함되며 방정식의 근이 됩니다.

답변.
,
.

• 음수가 아닌 표현식의 계수를 포함하는 방정식 풀기

실시예 11 방정식의 방정식 근(있는 경우 근)의 합은 얼마입니까?

해결책.표현을 고려해보세요

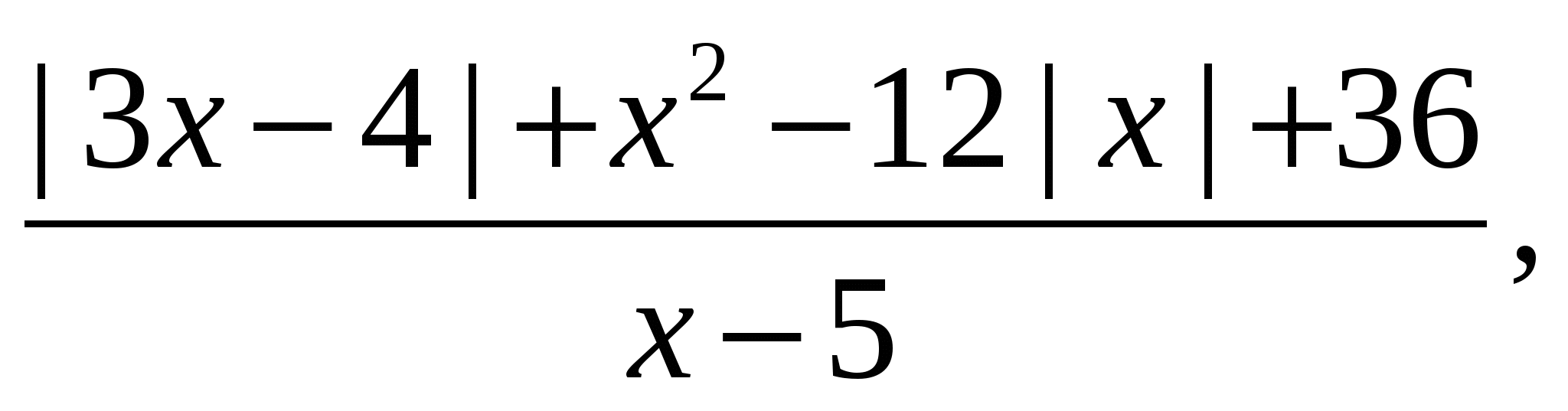그리고 이를 형식으로 변환합니다.

분수의 분자는 변수의 모든 값에 대해 양수임이 분명합니다. 이는 다음과 같은 경우 분수 표현식이 양수임을 의미합니다.
(왜냐하면
). 다음과 같이 결과 표현식을 변환해 보겠습니다.
. 우리는 원래의 방정식과 동등한 방정식을 얻습니다.

답변.
.

실시예 12 방정식을 풀어보세요

해결책.방정식의 왼쪽은 음수가 아니기 때문에 허용되는 모든 변수 값에 대해 방정식의 근 집합에서 오른쪽도 음수가 아니어야하므로 조건은 다음과 같습니다.
, 이 구간에서 두 분수의 분모는 동일하며 방정식을 풀어야 합니다.
. 이를 해결하고 제약 조건을 고려
, 우리는 얻는다

답변.
.

• 기하학적 해석을 사용하여 방정식 풀기

표현의 기하학적 의미
- 가로좌표와 점을 연결하는 좌표축 세그먼트의 길이 그리고 . 번역 대수 문제기하학적 언어를 사용하면 종종 번거로운 계산을 피할 수 있습니다.

실시예 13 방정식을 풀어보자
.

해결책.우리는 다음과 같이 추론할 것입니다: 모듈의 기하학적 해석을 기반으로 방정식의 왼쪽은 가로좌표를 사용하여 특정 지점으로부터의 거리의 합입니다. 가로좌표 1과 2가 있는 두 개의 고정점으로. 그런 다음 세그먼트의 가로좌표가 있는 모든 점
필요한 속성이 있지만 이 세그먼트 외부에 위치한 포인트는 없습니다.

답변.
.

실시예 14 불평등 해결
.

해결책.좌표선에 점을 그려 보겠습니다. 점에서 점까지의 거리의 합입니다.
그리고 정확히 같다 . 이들은 모두 세그먼트의 포인트입니다.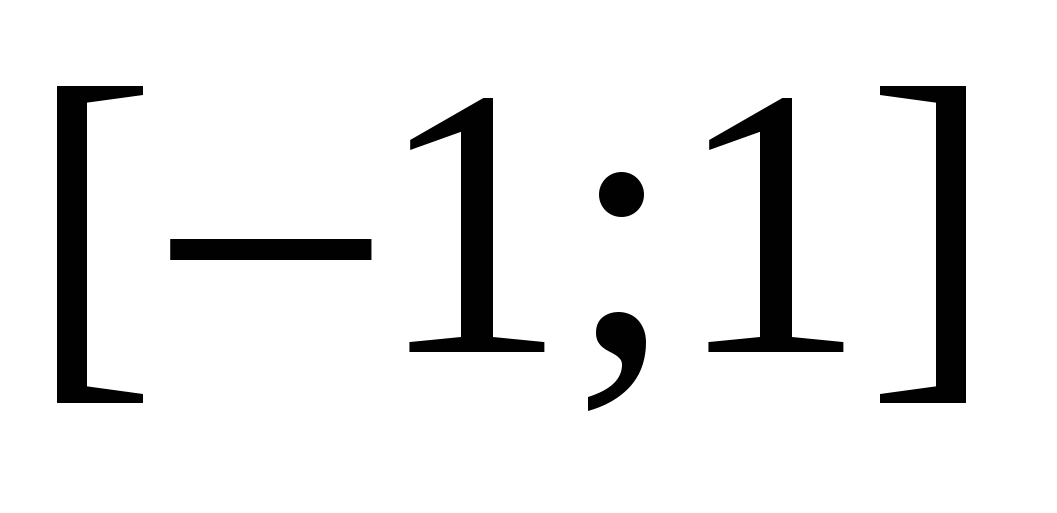
. 이 세그먼트 외부의 모든 숫자에 대해 거리의 합은 2보다 큽니다.

답변.
.

예(C3, 통합 상태 시험 - 2010) 15 방정식을 풀어보세요

해결책. ID를 두 번 적용
, 우리는 방정식을 얻습니다

그 해는 간격입니다
.

답변.
.

예(C3, 통합 상태 시험 - 2011) 16 17 방정식을 풀어보세요

해결책. .

답변.
.

• 방정식 풀이에 부호 정리 적용

모듈러스 차이의 곱이나 몫에 관한 부등식을 해결하는 데 편리한 정리를 공식화해 보겠습니다.

정리 18 두 표현식의 모듈러스 차이의 부호는 이러한 표현식의 제곱 차이의 부호와 일치합니다. 변수의 어떤 값에도 사라지지 않습니다. 이는 정의의 전체 영역에서 함수가 상수 부호를 갖는다는 것을 의미합니다. 예를 들어 계산하면 다음과 같습니다.
, 우리는 이 함수가 오직 양수 값.

답변.
.

간격 방법을 사용하면 더 많은 문제를 해결할 수 있습니다. 복잡한 방정식모듈과의 부등식이지만 이 경우에는 약간 다른 목적이 있습니다. 요점은 다음과 같습니다. 우리는 모든 하위 모듈 식의 근을 찾고 수치 축을 이러한 식의 상수 부호 간격으로 나눕니다. 이를 통해 이러한 간격을 순차적으로 진행함으로써 동시에 모든 모듈을 제거하고 일반 방정식 또는 부등식을 풀 수 있습니다(찾은 답이 이 간격에 포함되어 있는지 확인하면서).

• 양수를 곱하여 방정식 풀기

결론.

우리의 작업을 요약하면 다음과 같이 말할 수 있습니다.

연구의 목표는 모듈러스를 사용하여 방정식과 부등식을 해결하기 위한 다양한 방법을 연구하는 것이었습니다.

모듈러스의 합에 대한 정리뿐만 아니라 등가 전이를 사용하여 해결되는 가장 간단한 방정식 및 모듈러스 부등식의 일부 변형이 고려됩니다. 방정식을 푸는 그래픽 방식. 학교 수학 과정에서 이것이 가장 자주 사용되는 해결 방법이라고 말해야 합니다. 그래픽 방법은 문제를 해결할 때 특히 관련이 있습니다.기음 5 제어 및 측정 통합 상태 시험 자료.

다음으로, 우리는 여러 예를 사용하여 모듈을 사용하여 방정식과 부등식을 해결하는 다른 방법, 즉 모듈을 공개하는 방법을 연구했습니다. 음수가 아닌 표현식의 계수를 포함하는 방정식 풀기; 기하학적 해석을 사용하여 방정식 풀기; 신원을 사용하여
; 부호 정리의 적용; 결과로 이동하여 양의 요소를 곱하고 간격 방법으로 불평등을 해결하여 방정식을 해결합니다.

따라서 연구 중에 우리는 다음과 같은 결론에 도달했습니다.

우리는 모듈 공개 방법, 그래픽 방법 및 간격 방법이 가장 보편적이고 가장 많은 문제에 적용 가능한 방법이라고 생각합니다. 이 믿음은 결정의 결과로 발생했습니다. 큰 수통합 상태 시험, 과목 챔피언십, 올림피아드 문제의 자료 테스트 및 측정, 이 문제에 대한 문헌 연구 등의 작업을 수행합니다. 우리는 또한 아이덴티티에 대한 지식과 적용을 매우 중요하게 생각합니다.
, 방정식과 부등식을 푸는 것뿐만 아니라 근호를 사용하여 많은 표현을 변환하는 데에도 사용되기 때문입니다. 우리가 고려한 나머지 해결 방법은 수학적 지평 확대 및 일반 측면에서 확실히 큰 관심을 끌고 있습니다. 수학적 발달. 따라서 우리는 이를 통합 국가 시험 형태의 주 최종 인증 준비 및 고등 교육 기관에서의 학습 준비에 사용할 계획입니다.

사용된 문헌 목록입니다.

학생과 학생들을 위한 “큰 수학 백과사전”;

수학. 통합 상태 시험 - 2011, 2012. 모델 시험 옵션. / 편집자: A.L. 세메노바, I.V. 야쉬첸코.

M.Ya. Vygodsky. 초등수학 핸드북

"최신 학생 참고서";

백과사전 “나는 세계를 탐험합니다. 수학";

;

이 기사는 다음을 포함하는 다양한 방정식과 부등식을 해결하는 기술에 대해 다룹니다.
모듈러스 기호 아래의 변수입니다.

시험에서 계수가 있는 방정식이나 부등식을 발견하면 다음과 같이 해결할 수 있습니다.
특별한 방법을 전혀 모르고 모듈 정의만 사용합니다. 사실인가요?
귀중한 시험 시간이 한 시간 반 정도 걸릴 수 있습니다.

그래서 우리는 그러한 문제를 간단하게 해결하는 기술에 대해 이야기하고 싶습니다.

우선, 기억하자.

고려해 봅시다 다양한 유형 모듈러스가 있는 방정식. (나중에 불평등에 대해 다루겠습니다.)

왼쪽은 모듈, 오른쪽은 숫자

이것은 가장 간단한 경우입니다. 방정식을 풀어보자

모듈이 4인 숫자는 2개뿐입니다. 이는 4와 -4입니다. 따라서 방정식
두 가지 간단한 조합과 같습니다.

두 번째 방정식에는 해가 없습니다. 첫 번째 해법: x = 0 및 x = 5.

답: 0; 5.

모듈 아래 및 모듈 외부 모두 변수

여기서는 정의에 따라 모듈을 확장해야 합니다. . . 아니면 생각해보세요!

방정식은 모듈러스 아래 표현식의 부호에 따라 두 가지 경우로 나뉩니다.
즉, 두 시스템을 결합한 것과 같습니다.

첫 번째 시스템의 솔루션: . 두 번째 시스템에는 솔루션이 없습니다.
답: 1.

첫 번째 경우: x ≥ 3. 모듈 제거:

음수인 숫자는 x ≥ 3 조건을 충족하지 않으므로 원래 방정식의 근이 아닙니다.

만족하는지 알아보자 이 조건숫자 . 이를 위해 차이를 구성하고 그 부호를 결정합니다.

이는 3보다 크고 따라서 원래 방정식의 근이 됨을 의미합니다.

두 번째 경우: x< 3. Снимаем модуль:

숫자 . 보다 크므로 조건 x를 만족하지 않습니다.< 3. Проверим :

수단, . 는 원래 방정식의 근입니다.

정의에 따라 모듈을 제거하시겠습니까? 판별식이 완전제곱식이 아니기 때문에 생각하는 것조차 무섭습니다. 다음 고려 사항을 더 잘 활용해 봅시다: |A| 형식의 방정식 = B는 두 시스템의 조합과 동일합니다.

똑같지만 조금 다릅니다:

즉, 두 방정식 A = B와 A = −B를 푼 다음 B ≥ 0 조건을 만족하는 근을 선택합니다.

시작해 봅시다. 먼저 첫 번째 방정식을 푼다.

그런 다음 두 번째 방정식을 푼다.

이제 각 경우에 오른쪽의 부호를 확인합니다.

따라서 및 만 적합합니다.

대체 |x|를 사용한 이차 방정식 =t

방정식을 풀어 봅시다:

이므로 |x|를 바꾸는 것이 편리합니다. = 티. 우리는 다음을 얻습니다:

답: ±1.

모듈러스는 모듈러스와 같습니다.

우리는 |A| 형식의 방정식에 대해 이야기하고 있습니다. = |B|. 이것은 운명의 선물입니다. 정의에 따라 모듈 공개가 없습니다! 간단합니다:

예를 들어 다음 방정식을 고려하십시오. 이는 다음 세트와 동일합니다.

세트의 각 방정식을 풀고 답을 적는 것이 남아 있습니다.

두 개 이상의 모듈

방정식을 풀어 봅시다:

각 모듈을 별도로 신경쓰지 말고 정의에 따라 열어 보겠습니다. 옵션이 너무 많습니다. 보다 합리적인 방법, 즉 간격 방법이 있습니다.

모듈러스 표현식은 x = 1, x = 2 및 x = 3 지점에서 사라집니다. 이러한 지점은 수직선을 4개의 간격(간격)으로 나눕니다. 수직선에 이러한 점을 표시하고 결과 간격의 모듈 아래에 각 표현식에 대한 기호를 배치해 보겠습니다. (부호의 순서는 방정식에서 해당 모듈의 순서와 일치합니다.)

따라서 x가 각 구간에 있는 네 가지 경우를 고려해야 합니다.

사례 1: x ≥ 3. 모든 모듈은 "+"로 제거됩니다.

결과 값 x = 5는 조건 x ≥ 3을 충족하므로 원래 방정식의 근이 됩니다.

사례 2: 2 ≤ x ≤ 3. 이제 마지막 모듈이 "마이너스"와 함께 제거됩니다.

x의 결과 값도 적합합니다. 이는 고려 중인 구간에 속합니다.

사례 3: 1 ≤ x ≤ 2. 두 번째 및 세 번째 모듈은 "마이너스로" 제거됩니다.

우리는 고려 중인 구간에서 모든 x에 대해 정확한 수치적 동등성을 얻었습니다. 이는 이 방정식의 해로 사용됩니다.

사례 4: x ≤ 1 ≤ 1. 두 번째 및 세 번째 모듈은 "마이너스"로 제거됩니다.

새로운 것은 없습니다. 우리는 이미 x = 1이 해라는 것을 알고 있습니다.

답: ∪ (5).

모듈 내의 모듈

방정식을 풀어 봅시다:

내부 모듈을 여는 것부터 시작합니다.

1) x ≤ 3. 우리는 다음을 얻습니다:

모듈러스 아래의 표현식은 에서 사라집니다. 이 점은 고려된 점에 속합니다.
사이. 그러므로 우리는 두 가지 하위 사례를 분석해야 합니다.

1.1) 이 경우 다음을 얻습니다.

이 x 값은 고려 중인 구간에 속하지 않으므로 적합하지 않습니다.

1.2) . 그 다음에:

이 x 값도 좋지 않습니다.

따라서 x ≤ 3에 대해서는 해가 없습니다. 두 번째 사례로 넘어가겠습니다.

2) x ≥ 3. 우리는 다음을 가집니다:

여기서 우리는 운이 좋습니다: x + 2 표현식은 고려 중인 구간에서 양수입니다! 따라서 더 이상 하위 사례가 없습니다. 모듈은 "플러스"로 제거됩니다.

이 x 값은 고려 중인 구간에 있으므로 원래 방정식의 근이 됩니다.

이것이 이 유형의 모든 문제가 해결되는 방법입니다. 내부 모듈부터 시작하여 중첩 모듈을 하나씩 엽니다.

불평등 해결책모드에서 온라인 해결책거의 모든 불평등 온라인. 매우 정확한 온라인 불평등수학을 해결하기 위해. 빠르게 찾기 불평등 해결책모드에서 온라인. www.site 웹사이트에서 다음을 찾을 수 있습니다. 해결책거의 모든 주어진 대수학, 삼각법또는 온라인의 초월적 불평등. 다양한 단계에서 수학의 거의 모든 분야를 공부할 때 다음 사항을 결정해야 합니다. 온라인 불평등. 즉시 답변을 얻으려면, 가장 중요하게는 정확한 답변을 얻으려면 이를 수행할 수 있는 리소스가 필요합니다. 사이트 www.site 덕분에 불평등을 온라인으로 해결하다몇 분 정도 걸립니다. 수학 문제를 해결할 때 www.site의 주요 이점 온라인 불평등- 제공되는 응답의 속도와 정확성입니다. 이 사이트는 모든 것을 해결할 수 있습니다 온라인 대수적 불평등, 온라인 삼각 부등식, 온라인의 초월적 불평등, 그리고 또한 불평등모드에 알 수 없는 매개변수가 있는 경우 온라인. 불평등강력한 수학적 장치 역할을 함 솔루션실용적인 문제. 도움으로 수학적 불평등언뜻 보면 혼란스럽고 복잡해 보일 수 있는 사실과 관계를 표현하는 것이 가능합니다. 수량을 알 수 없음 불평등문제를 공식화함으로써 찾을 수 있다. 매우 정확한형태의 언어 불평등그리고 결정하다모드에서 작업을 받았습니다 온라인웹사이트 www.site에서. 어느 대수적 부등식, 삼각 부등식또는 불평등포함하는 탁월한쉽게 할 수 있는 기능 결정하다온라인으로 정확한 답변을 받아보세요. 자연과학을 공부하다 보면 필연적으로 불평등에 대한 해결책. 이 경우 답변은 정확해야 하며 해당 모드에서 즉시 답변을 받아야 합니다. 온라인. 그러므로 온라인으로 수학적 불평등을 해결하세요우리는 귀하에게 없어서는 안될 계산기가 될 www.site 사이트를 추천합니다. 대수적 부등식을 온라인으로 해결하기, 온라인 삼각 부등식, 그리고 또한 온라인의 초월적 불평등또는 불평등알 수 없는 매개변수를 사용합니다. 다양한 문제에 대한 온라인 솔루션을 찾는 실제적인 문제 수학적 불평등자원 www.. 해결 온라인 불평등다음을 사용하여 받은 답변을 확인하는 것이 유용합니다. 온라인 솔루션불평등웹사이트 www.site에서. 불평등을 올바르게 작성하고 즉시 얻어야합니다. 온라인 솔루션, 그 후에 남은 것은 답을 불평등에 대한 해결책과 비교하는 것입니다. 답변을 확인하는 데는 1분도 걸리지 않습니다. 충분합니다. 불평등을 온라인으로 해결하다그리고 답을 비교해 보세요. 이렇게 하면 실수를 방지하는 데 도움이 됩니다. 결정그리고 시간에 맞춰 답을 수정하세요. 불평등을 온라인으로 해결하다그럴 수도 있지 대수학, 삼각법, 탁월한또는 불평등알 수 없는 매개변수를 사용합니다.

수학 과학의 지혜의 상징이다,

과학적 엄격함과 단순함의 모델,

과학의 우수성과 아름다움의 기준.

러시아 철학자 A.V. 볼로시노프

모듈러스와의 부등식

학교 수학에서 가장 풀기 어려운 문제는 불평등이다, 모듈러스 기호 아래에 변수가 포함되어 있습니다. 이러한 불평등을 성공적으로 해결하려면 모듈의 속성에 대한 충분한 지식과 이를 활용할 수 있는 기술이 있어야 합니다.

기본 개념 및 속성

실수의 계수(절대값)로 표시 다음과 같이 정의됩니다.

모듈의 단순 속성에는 다음 관계가 포함됩니다.

그리고 .

메모, 마지막 두 속성은 모든 짝수 차수에 유효합니다.

더욱이, 만약, 어디서, 그러면 그리고

더 복잡한 속성기준 치수, 모듈러스를 사용하여 방정식과 부등식을 풀 때 효과적으로 사용할 수 있습니다., 다음 정리를 통해 공식화됩니다.

정리 1.모든 분석 기능의 경우그리고 불평등은 사실이다.

정리 2.평등 불평등과 다름없다.

정리 3.평등 불평등과 다름없다.

학교 수학에서 가장 흔한 불평등, 모듈러스 기호 아래에 알 수 없는 변수가 포함되어 있음, 형태의 불평등이다그리고, 어디서 일부 양의 상수.

정리 4.불평등 이중 불평등과 동일, 그리고 불평등의 해결책일련의 불평등을 해결하는 것으로 축소됩니다.그리고 .

이 정리는 정리 6과 7의 특별한 경우입니다.

더 복잡한 불평등, 모듈을 포함하는 것은 다음 형식의 부등식입니다., 그리고 .

이러한 부등식을 해결하는 방법은 다음 세 가지 정리를 사용하여 공식화될 수 있습니다.

정리 5.불평등 두 불평등 시스템을 결합한 것과 동일합니다.

나는 (1)

증거.그 이후로

이는 (1)의 타당성을 의미합니다.

정리 6.불평등 불평등 시스템과 동일합니다.

증거.왜냐하면 , 그럼 불평등에서그것은 다음과 같습니다 . 이 조건에서 불평등은그리고 이 경우 두 번째 불평등 시스템(1)은 일관성이 없는 것으로 판명될 것입니다.

정리가 입증되었습니다.

정리 7.불평등 하나의 불평등과 두 개의 불평등 시스템을 결합한 것과 같습니다.

나는 (3)

증거.이후 , 그러면 부등식 항상 실행, 만약에 .

허락하다 그러면 불평등불평등과 같을 것이다, 두 부등식의 집합을 따르는 것그리고 .

정리가 입증되었습니다.

불평등이라는 주제에 대한 문제 해결의 전형적인 예를 살펴 보겠습니다., 모듈러스 기호 아래에 변수가 포함되어 있습니다."

모듈러스로 부등식 풀기

모듈러스로 부등식을 해결하는 가장 간단한 방법은 다음과 같습니다., 모듈 확장을 기반으로 합니다. 이 방법은 보편적입니다, 그러나 일반적인 경우에는 이를 사용하면 매우 번거로운 계산이 발생할 수 있습니다. 그러므로 학생들은 그러한 불평등을 해결하기 위한 다른 (보다 효과적인) 방법과 기술을 알아야 합니다. 특히, 정리를 적용하는 기술이 필요합니다, 이 기사에 나와 있습니다.

예시 1.불평등 해결

. (4)

해결책.우리는 모듈을 드러내는 방법인 "고전적인" 방법을 사용하여 불평등(4)을 해결할 것입니다. 이를 위해 숫자 축을 나눕니다.점과 간격으로 나누고 세 가지 경우를 고려하십시오.

1. 만약 , 그렇다면 , , , 불평등 (4)는 다음과 같은 형태를 취합니다.또는 .

여기서 사례를 고려하면 불평등에 대한 해결책이 된다(4).

2. 만일, 그런 다음 불평등 (4)로부터 우리는 다음을 얻습니다.또는 . 간격의 교차 이후그리고 비어있다, 그러면 고려 중인 솔루션 간격에는 불평등이 없습니다(4).

3. 만일, 그러면 불평등(4)은 다음과 같은 형태를 취합니다.또는 . 그것은 분명하다 불평등에 대한 해결책이기도 하다(4).

답변: , .

예시 2.불평등 해결.

해결책.가정해보자. 왜냐하면 , 그러면 주어진 부등식은 다음과 같은 형태를 취합니다또는 . 그 이후로 그리고 여기에서 다음과 같습니다또는 .

그러나 그러므로 또는.

예시 3.불평등 해결

. (5)

해결책.왜냐하면 , 그러면 불평등(5)은 불평등과 동일합니다.또는 . 여기에서, 정리 4에 따르면, 우리에게는 일련의 불평등이 있습니다그리고 .

답변: , .

예시 4.불평등 해결

. (6)

해결책.을 나타내자. 그런 다음 부등식 (6)에서 부등식 , , 또는 을 얻습니다.

여기에서, 간격 방법을 사용하여, 우리는 얻습니다. 왜냐하면 , 그러면 여기에 불평등의 시스템이 있습니다

시스템 (7)의 첫 번째 부등식에 대한 해는 두 구간의 합집합입니다.그리고 , 두 번째 불평등에 대한 해결책은 이중 불평등입니다.. 이는 다음과 같습니다. 불평등 연립방정식(7)의 해는 두 간격의 합집합이라는 것그리고 .

답변: ,

실시예 5.불평등 해결

. (8)

해결책. 불평등(8)을 다음과 같이 변환해 보겠습니다.

또는 .

간격 방법 사용, 우리는 불평등에 대한 해결책을 얻습니다(8).

답변: .

메모. 정리 5의 조건에 와 를 대입하면 을 얻습니다.

예시 6.불평등 해결

. (9)

해결책. 불평등 (9)로부터 다음과 같다. 불평등(9)을 다음과 같이 변형해 보겠습니다.

또는

이후 , 그때 또는 .

답변: .

실시예 7.불평등 해결

. (10)

해결책.이후 및 , 다음 또는 .

이와 관련하여 불평등 (10)은 다음과 같은 형태를 취합니다.

또는

. (11)

그것은 또는 . 이후 불평등 (11)은 또는 을 의미합니다.

답변: .

메모. 부등식의 좌변에 정리 1을 적용하면 (10), 그러면 우리는 얻는다 . 이것과 불평등(10)으로부터 다음과 같다, 무엇 또는 . 왜냐하면 , 그러면 불평등(10)은 다음과 같은 형태를 취합니다.또는 .

실시예 8.불평등 해결

. (12)

해결책.그 이후로 그리고 불평등 (12)으로부터 다음과 같습니다또는 . 그러나 그러므로 또는. 여기에서 우리는 또는 를 얻습니다.

답변: .

실시예 9.불평등 해결

. (13)

해결책.정리 7에 따르면 불평등(13)에 대한 해는 다음과 같습니다.

지금 그대로 두십시오. 그런 경우에는 불평등 (13)은 다음과 같은 형태를 취합니다.또는 .

간격을 합치면그리고 , 그런 다음 우리는 다음 형식의 불평등(13)에 대한 해결책을 얻습니다..

실시예 10.불평등 해결

. (14)

해결책.불평등(14)을 동등한 형식으로 다시 작성해 보겠습니다. 이 부등식의 좌변에 정리 1을 적용하면 부등식 을 얻습니다.

여기와 정리 1로부터 다음과 같습니다., 부등식(14)은 모든 값에 대해 충족됩니다..

대답: 임의의 숫자.

실시예 11.불평등 해결

. (15)

해결책. 부등식의 좌변에 정리 1 적용(15), 우리는 얻는다 . 이것과 부등식(15)은 다음 방정식을 산출합니다., 이는 다음과 같은 형태를 가지고 있습니다..

정리 3에 따르면, 방정식 불평등과 다름없다. 여기에서 우리는 얻는다.

실시예 12.불평등 해결

. (16)

해결책. 불평등 (16)으로부터 정리 4에 따라 우리는 불평등 시스템을 얻습니다.

불평등을 해결할 때정리 6을 사용하여 부등식 시스템을 구해 보겠습니다.그로부터 다음과 같은.

불평등을 고려하라. 정리 7에 따르면, 우리는 일련의 불평등을 얻습니다그리고 . 두 번째 인구 불평등은 모든 실제 상황에 유효합니다..

따라서 , 불평등에 대한 해결책(16)은 다음과 같습니다..

실시예 13.불평등 해결

. (17)

해결책.정리 1에 따르면 다음과 같이 쓸 수 있습니다.

(18)

불평등(17)을 고려하여 우리는 두 불평등(18)이 모두 평등으로 변한다는 결론을 내립니다. 방정식 시스템이 있습니다

정리 3에 따르면 이 방정식 시스템은 부등식 시스템과 동일합니다.

또는

실시예 14.불평등 해결

. (19)

해결책.그때부터. 불평등 (19)의 양쪽에 어떤 값에 대해 양수 값만 취하는 표현식을 곱해 봅시다. 그런 다음 불평등(19)과 동일한 불평등을 얻습니다.

여기에서 우리는 or , where 를 얻습니다. 이후와 그러면 불평등(19)에 대한 해결책은 다음과 같습니다.그리고 .

답변: , .

모듈러스를 사용하여 불평등을 해결하는 방법에 대한 보다 심층적인 연구를 위해서는 교과서를 참조하는 것이 좋습니다., 추천 문헌 목록에 나와 있습니다.

1. 대학 지원자를 위한 수학 문제 모음 / Ed. 미. 스카나비. – M.: 평화와 교육, 2013. – 608p.

2. 수프런 V.P. 고등학생을 위한 수학: 불평등을 해결하고 증명하는 방법. – M.: 레넌드 / URSS, 2018. – 264p.

3. 수프런 V.P. 고등학생을 위한 수학: 문제 해결을 위한 비표준 방법. – M.: CD “Librocom” / URSS, 2017. – 296p.

아직도 질문이 있으신가요?

튜터의 도움을 받으려면 등록하세요.

웹사이트에서 자료의 전체 또는 일부를 복사하는 경우 출처에 대한 링크가 필요합니다.